이 글의 원문은 https://opencv-python-tutroals.readthedocs.io/en/latest/py_tutorials/py_photo/py_non_local_means/py_non_local_means.html 입니다.
이 글에서는 이미지 안의 잡음을 제거하기 위해 Non-local Means 잡음제거 알고리즘에 대해 살펴봅니다. 이를 위한 OpenCV에서 제공하는 cv2.fastNlMeansDenoising(), cv2.fastNlMeansDenoisingColored() 등과 같은 함수들의 차이점에 대해서도 살펴봅니다.
이전 글에서, 가우시안 블러링, 메디안 블러링 등과 같은 이미지를 부드럽게 만드는 기법에 대해 살펴 보았으며, 이런 연산이 어느 정도의 잡음을 제거할 수 있었음을 보였습니다. 이들 방식은, 픽셀 주위의 다른 픽셀들 몇개를 취해 값들의 평균값등으로 원래의 값을 변경합니다. 요약하면, 이런 방식의 잡음 제거는 자신의 이웃에 한해서만 이루어집니다.
잡음에는 어떤 성질이 있습니다. 잡음은 일반적으로 제로 평균(Zero Mean)을 가진 무작위로 생겨납니다. 잡음 픽셀, ![]() 을 살펴봅시다.
을 살펴봅시다. ![]() 는 픽셀의 참 값이고
는 픽셀의 참 값이고 ![]() 은 그 픽셀의 잡음입니다. 다른 이미지들에서 동일한 픽셀들을(
은 그 픽셀의 잡음입니다. 다른 이미지들에서 동일한 픽셀들을(![]() 이라 합시다) 많이 취해서, 이들의 평균을 계산합니다. 이상적으로는 잡음의 평균은 0이므로
이라 합시다) 많이 취해서, 이들의 평균을 계산합니다. 이상적으로는 잡음의 평균은 0이므로 ![]() 이여야 합니다.
이여야 합니다.
간단한 설정을 통해 이것을 확인할 수 있습니다. 고정 카메라를 어떤 위치에 몇초간 놓습니다. 그러면 동일한 장면에 대한 많은 이미지 또는 프레임을 얻을 수 있겠죠. 그러고는 찍힌 모든 프레임의 평균을 구하는 코드를 작성합니다. 첫번째 프레임과 최종 결과를 비교해 봅시다. 잡음이 감소된 것을 볼 수 있을 것입니다. 불행히도 이 간단한 방법은 카메라와 움직이는 장면에 대해서는 적용하기 어렵습니다.
아이디어는 간단한데, 비슷한 이미지에 대한 잡음의 평균값들이 필요합니다. 이미지에서 작은 윈도우(5×5 크기로 합시다)를 고려해 봅시다. 하나의 이미지 안에는 동일한 조각이 다른 위치 여러 곳에 존재할 가능성이 큽니다. 때때로 조각 근처에 나타날 수 있습니다. 이러한 유사한 조각들을 활용해서 이들의 평균을 구한다면 어떨까요? 아래의 그림을 봅시다.
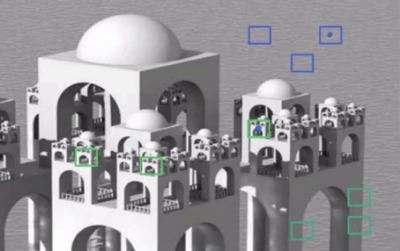
이미지에서 파란색 조각들은 유사해 보입니다. 파란색 조각도 유사해 보이죠. 이러한 픽셀을 취해, 이 픽셀 주위에 작은 윈도우를 만들어, 이미지에서 유사한 윈도우 영역을 찾아서, 모든 윈도우들의 평균을 내고, 그 평균 결과로 픽셀을 교체합니다. 이 방법이 NonLocal Means Denosing(잡음제거)이라고 합니다. 앞서 봤던 블러링(Burring) 기법과 비교하면 시간은 더 소요되지만, 결과는 매우 좋습니다.
칼라 이미지에 대해서, 이미지를 CIELAB 칼라공간(Colorspace)로 변경하고 L과 AB 요소에 대해 별도로 잡음을 제거 합니다.
이런 방법에 대해서 OpenCV에서는 4가지 방식을 제공합니다.
- cv2.fastNlMeansDenoising() – 그레이 이미지 하나에 대해서만 작동함
- cv2.fastNlMeansDenoisingColored() – 칼라 이미지 하나에 대해서 작동함
- cv2.fastNlMeansDenoisingMulti() – 짧은 시간 동안 찍힌 여러 개의 이미지에 대해서 작동하며 그레이 이미지여야 함
- cv2.fastNlMeansDenoisingColoredMulti() – 짧은 시간 동안 찍한 여러 개의 이미지에 대해서 작동하며 칼라 이미지에서 작동함
위 함수들의 공통 인자는 다음과 같습니다.
- h : 필터 강도를 결정하는 인자. 더 높은 h 값이 잡음을 더 잘 제거하지만 잡음이 아닌 픽셀도 제거함(10이면 적당함)
- hForColorComponents : h와 동일하지만, 칼라 이미지에 대해서만 사용됨(보통 h와 같음)
- templateWindowSize : 홀수값이여야 함(7을 권장함)
- searchWindowSize : 홀수값이여야 함(21을 권장함)
이 글에서는 2번과 3번에 대한 예제를 살펴 봅니다.
1. cv2.fastNlMeansDenoisingColored()
앞서 언급했듯이 칼라 이미지로부터 잡음을 제거 하는데 사용됩니다. 코드는 아래와 같습니다.
import numpy as np
import cv2
from matplotlib import pyplot as plt
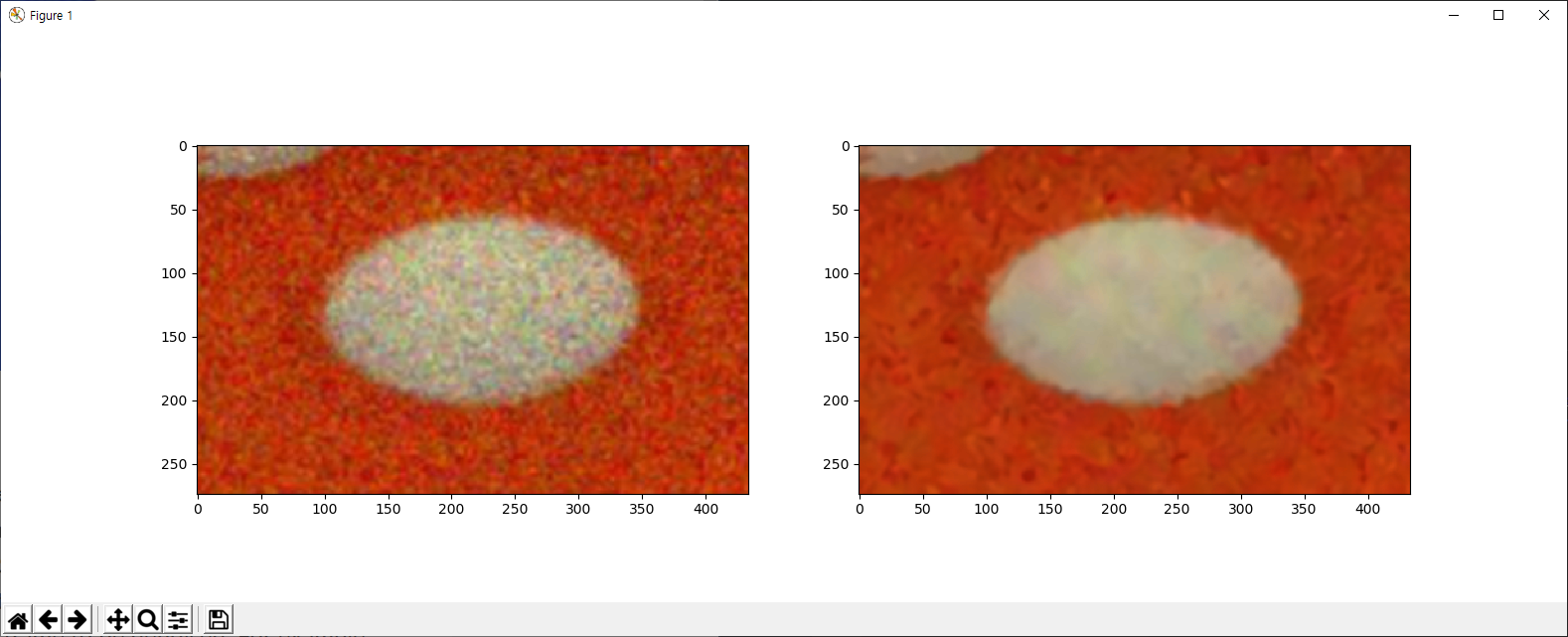
img = cv2.imread('./data/die.png')
dst = cv2.fastNlMeansDenoisingColored(img,None,10,10,7,21)
plt.subplot(121),plt.imshow(img)
plt.subplot(122),plt.imshow(dst)
plt.show()
아래는 결과인데, 입력 이미지는 ![]() 인 가우시안 잡음을 가지고 있습니다.
인 가우시안 잡음을 가지고 있습니다.
2. cv2.fastNlMeansDenoisingMulti()
이제 비디오에 대해서도 동일한 방법을 적용해 봅시다. 첫번째 인자는 잡음이 들어간 프레임 리스트입니다. 두번재 인자 imgToDenoiseIndex는 잡음을 제거할 프레임의 인덱스인데, 이를 위해 입력 리스트에 프레임 인덱스를 전달합니다. 세번째 인자는 temporalWindowSize으로 잡음 제거를 위해 사용할 인근 프레임의 개수입니다. 이 값은 홀수여야 합니다. 예제는 다음과 같습니다.
import numpy as np
import cv2
from matplotlib import pyplot as plt
cap = cv2.VideoCapture('./data/TownCentreXVID.mp4')
# create a list of first 5 frames
img = [cap.read()[1] for i in range(5)]
# convert all to grayscale
gray = [cv2.cvtColor(i, cv2.COLOR_BGR2GRAY) for i in img]
# convert all to float64
gray = [np.float64(i) for i in gray]
# create a noise of variance 25
noise = np.random.randn(*gray[1].shape)*10
# Add this noise to images
noisy = [i+noise for i in gray]
# Convert back to uint8
noisy = [np.uint8(np.clip(i,0,255)) for i in noisy]
# Denoise 3rd frame considering all the 5 frames
dst = cv2.fastNlMeansDenoisingMulti(noisy, 2, 5, None, 4, 7, 35)
plt.subplot(131),plt.imshow(gray[2],'gray')
plt.subplot(132),plt.imshow(noisy[2],'gray')
plt.subplot(133),plt.imshow(dst,'gray')
plt.show()
결과는 다음과 같습니다.

계산에 소요되는 시간이 상당한데, 첫번째 이미지는 원본 프레임이고 두번째는 잡음을 넣은 것이며 마지막은 두번째 이미지에 대한 잡음을 제거한 것입니다.