Python과 OpenCV – 52 : OpenCV에서 K-Means 군집화(Clustering)

이 글의 원문은 https://opencv-python-tutroals.readthedocs.io/en/latest/py_tutorials/py_ml/py_kmeans/py_kmeans_opencv/py_kmeans_opencv.html 입니다.

OpenCV에서 K-Means 알고리즘을 이용한 데이터 군집화는 cv2.kmeans() 함수를 통해 이용 됩니다. 이 함수에 대한 인자는 다음과 같습니다.

1. samples : np.float32 데이타 타입이며, 각 피쳐(Feature)는 단일 열(Column)으로 저장되어져 있어야 합니다.
2. nclusters(K) : 군집화할 개수
3. criteria : 반복을 종료할 조건입니다. 조건이 만족되면 알고리즘의 반복은 중지됩니다. 3개의 인자를 갖는 튜플(Tuple)이며, (type, max_iter, epsilon)입니다. 각각의 대한 인자는 다음과 같습니다.
   • type : 종료 조건의 타입으로 cv2.TERM_CRITERIA_EPS는 주어진 정확도(epsilon 인자)에 도달하면 반복을 중단하고, cv2.TERM_CRITERIA_MAX_ITER는 max_iter 인자에 지정된 횟수만큼 반복하고 중단합니다. cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER를 조합해 사용하면 두가지 조건 중 하나가 만족되면 반복이 중단됩니다.
   • max_iter : 최대 반복할 횟수(정수형 타입)
   • epsilon : 정확도
4. attempts : 다른 초기 라벨링을 사용하면서 실행되는 알고리즘의 실행 횟수를 지정하는 플래그. 알고리즘은 최적의 컴팩트함(Compactness)을 만드는 라벨을 반환합니다. 이 컴팩트함은 출력으로 반환됩니다.
5. flags : 초기값을 잡을 중심에 대한 플래그로써 cv2.KMEANS_PP_CENTERS와 cv2.KMEANS_RANDOM_CENTERS 중 하나가 사용됩니다.

이 함수의 반환값은 다음과 같습니다.

1. compactness : 각 포인트와 군집화를 위한 중심 간의 거리의 제곱의 합
2. labes : 라벨에 대한 배열이며, ‘0’, ‘1’ 같이 이전 글에서 언급한 내용과 같음.
3. centers : 클러스터의 중심이 저장된 배열

이제 3가지 예를 통해 K-Means 알고리즘이 어떻게 OpenCV에서 사용되는지 살펴봅시다.

1. 하나의 특징(Feature)을 가지는 데이터

오직 하나의 특징을 가지는 데이터, 예를 들어 1차원 데이터 셋을 봅시다. 그러니까 T셔츠의 크기를 결정하기 위해 사람의 키에 대한 특징만을 고려하는 것입니다.

데이터를 생성하고 Matplotlib으로 표시해 보면..

import numpy as np
import cv2
from matplotlib import pyplot as plt

x = np.random.randint(25,100,25) 
y = np.random.randint(175,255,25)
z = np.hstack((x,y))
z = z.reshape((50,1))
z = np.float32(z)
plt.hist(z,256,[0,256]),plt.show()

크기 50개의 배열 z가 있으며, 구성 요소의 값은 0~255 사이입니다. z를 단일 열(column)로 구성합니다. 마지막으로 데이터의 타입을 np.float32로 변환합니다. 결과는 다음과 같습니다.

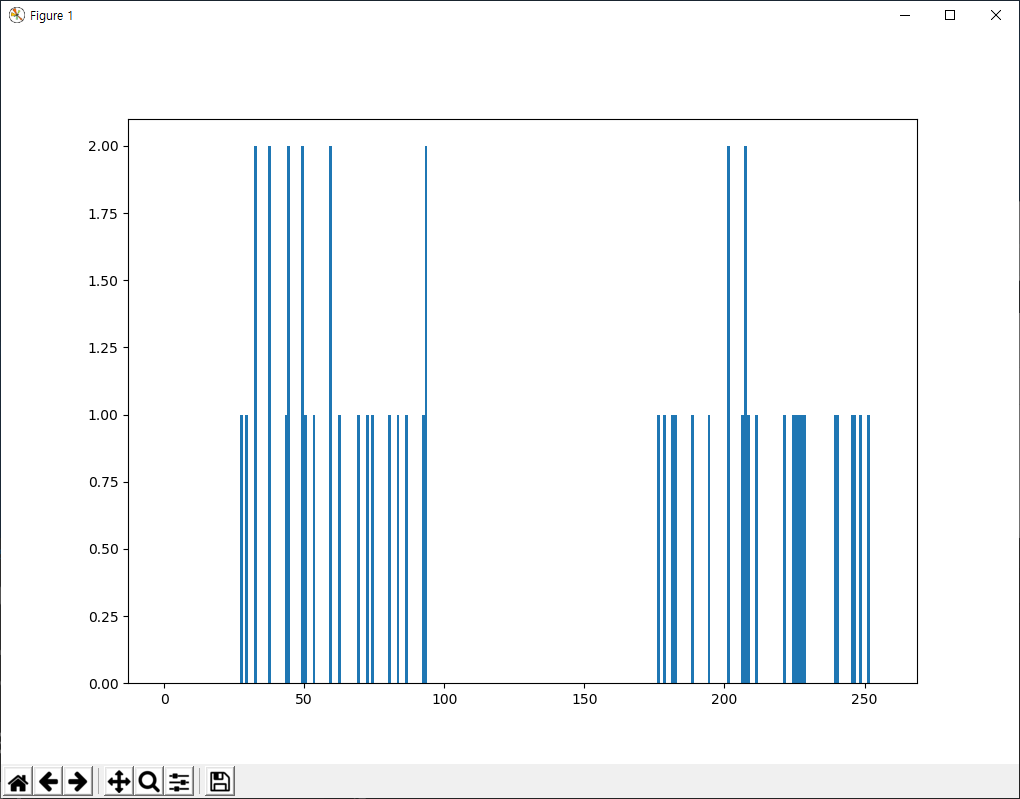
이제, K-Means 함수를 적용해 봅시다. 알고리즘 종료에 대한 기준 조건을 정해야 합니다. 여기서 기준은 10반 반복과 정확도(epsilon)은 1.0으로 정합니다.

# Define criteria = ( type, max_iter = 10 , epsilon = 1.0 )
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 10, 1.0)

# Set flags (Just to avoid line break in the code)
flags = cv2.KMEANS_RANDOM_CENTERS

# Apply KMeans
compactness,labels,centers = cv2.kmeans(z,2,None,criteria,10,flags)

위 예제의 cv2.kmeans 함수는 compactness와 labels, centers 변수에 반환값을 넘겨줍니다. 이 경우 centers는 57.92과 114.5이며, labels에는 각 요소에 대해 ‘0’, ‘1’ 중에 하나의 값으로 분류된 라벨값입니다. 여기서 이 라벨값을 기반으로 데이터를 A와 B 변수로 나눠봅시다.

A = z[labels==0]
B = z[labels==1]

그리고 A와 B를 각각 파란색과 빨간색으로 표시하고, 군집화된 중심을 노란색으로 표시해 봅시다.

# Now plot 'A' in red, 'B' in blue, 'centers' in yellow
plt.hist(A,256,[0,256],color = 'r')
plt.hist(B,256,[0,256],color = 'b')
plt.hist(centers,32,[0,256],color = 'y')
plt.show()

결과는 아래와 같습니다.

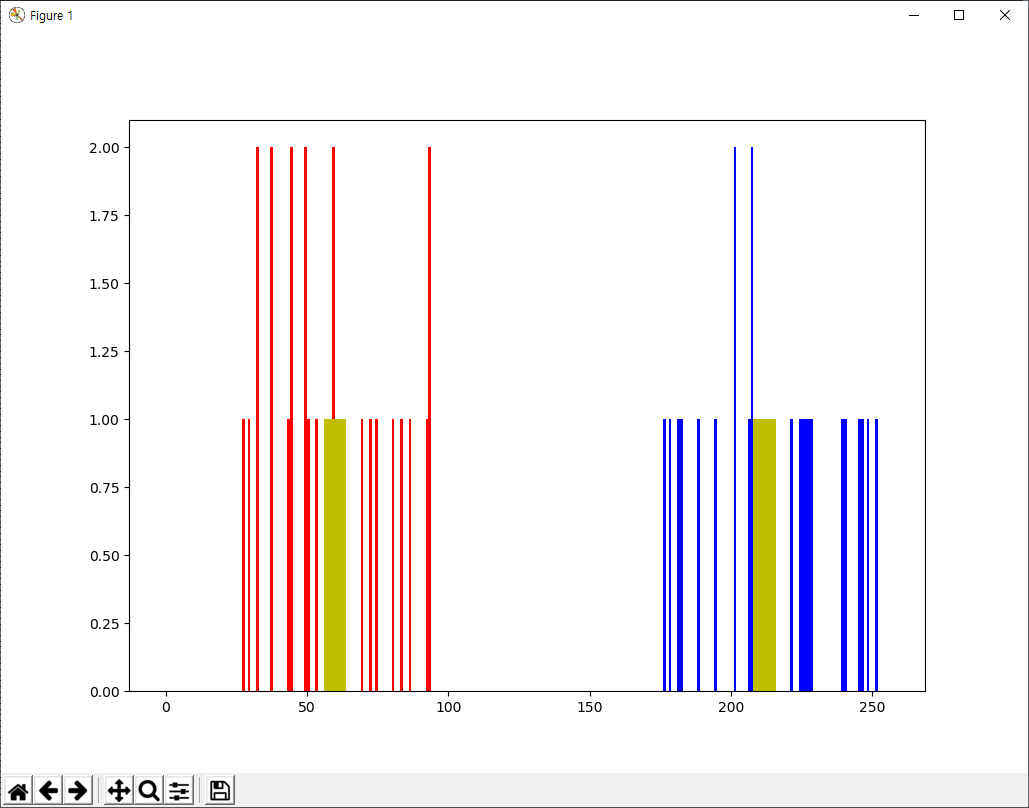
2. 여러 개의 특징(Feature)을 가지는 데이터

이전 예에서, T셔츠에 대해 오직 키에 대한 특징점만을 고려했습니다. 여기서는 키와 몸무게처럼 2개의 특징점을 고려해 봅시다.

이전 경우에서, 입력 데이터를 단일 열(column) 벡터로 구성했다는 것을 기억해야 합니다. 각 특징은 열로 정렬되어 잇어야 합니다. 예를 들어서, 이 경우 50명의 사람에 대해 키와 몸무게 값으로 구성된 50×2 크기의 테스트 데이터를 구성합니다. 첫번째 열(Column)은 50명에 대한 키 값이고 두번째 열은 이들의 키값입니다. 첫번째 행(Row)는 첫번째 사람의 키와 몸무게 값입니다. 즉, 아래 그림과 같은 구성입니다.

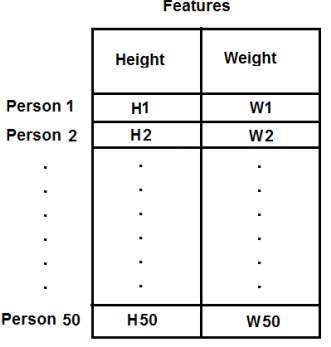
바로 코드를 보면..

import numpy as np
import cv2
from matplotlib import pyplot as plt

X = np.random.randint(25,50,(25,2))
Y = np.random.randint(60,85,(25,2))
Z = np.vstack((X,Y))

# convert to np.float32
Z = np.float32(Z)

# define criteria and apply kmeans()
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 10, 1.0)
ret,label,center=cv2.kmeans(Z,2,None,criteria,10,cv2.KMEANS_RANDOM_CENTERS)

# Now separate the data, Note the flatten()
A = Z[label.ravel()==0]
B = Z[label.ravel()==1]

# Plot the data
plt.scatter(A[:,0],A[:,1])
plt.scatter(B[:,0],B[:,1],c = 'r')
plt.scatter(center[:,0],center[:,1],s = 80,c = 'y', marker = 's')
plt.xlabel('Height'),plt.ylabel('Weight')
plt.show()

결과는 다음과 같습니다.

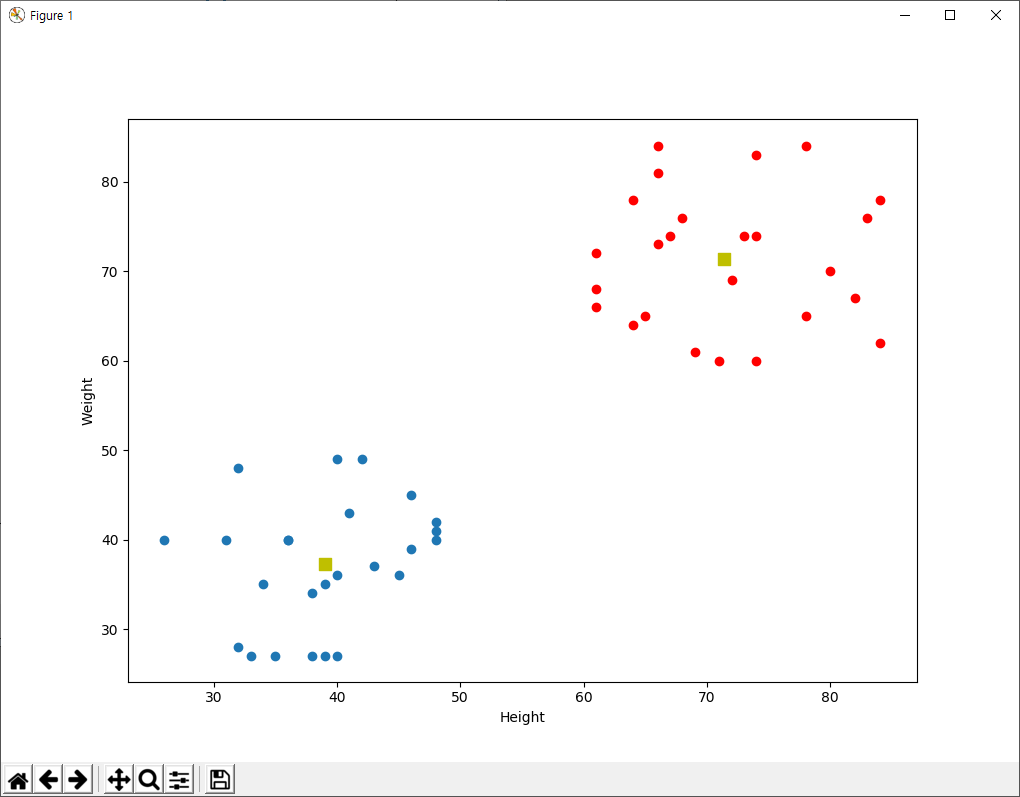
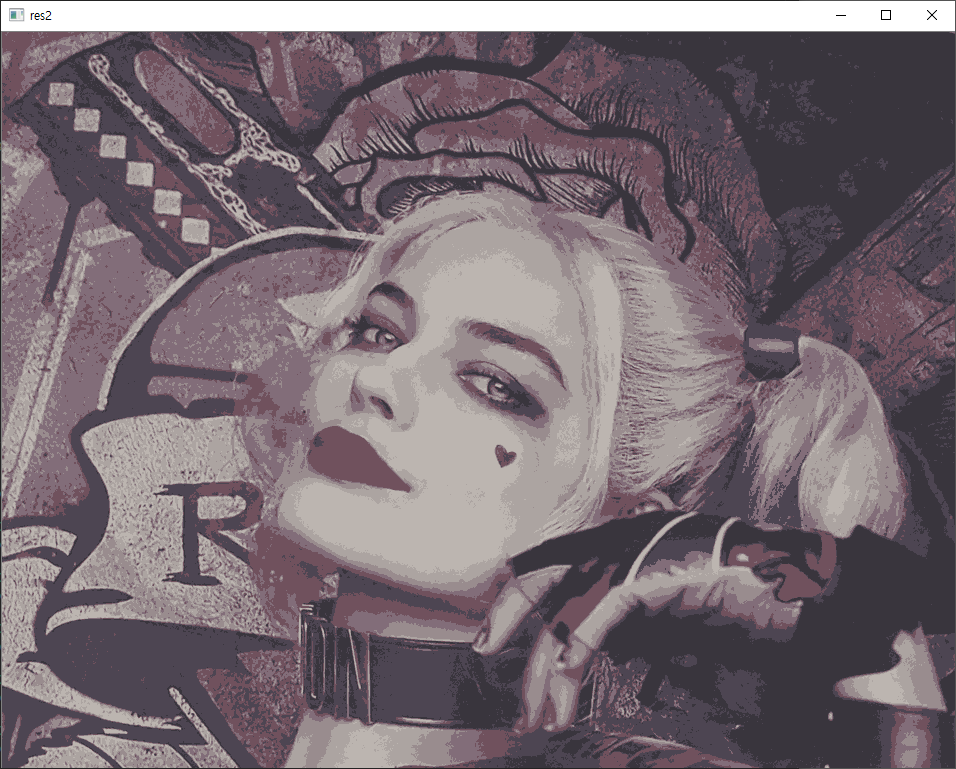
3. 색상 양자화(Color Quantization)

색상 양자화는 이미지에서 사용하는 색상의 수를 줄이는 처리입니다. 이러한 처리를 하는 목적 중 하나는 사용하는 메모리를 줄이기 위해서입니다. 색상 양자화를 위해 K-Means 클러스터링을 활용해 보겠습니다.

새롭게 추가되는 새로운 내용은 없습니다. 특징점은 3개인데, 바로 R, G, B입니다. 이미지의 화소 데이터를 Mx3 배열로 만다는데, M은 이미지의 화소 개수입니다. 클러스터링 이후에, 중심점(이 값 역시도 R, G, B 임)값으로 해당 소속되는 화소의 값을 변경합니다. 그리고 다시 Mx3 배열을 원래 이미지의 크기로 재구성하면 됩니다. 코드는 다음과 같습니다.

import numpy as np
import cv2

img = cv2.imread('./data/harleyQuinnA.jpg')
Z = img.reshape((-1,3))

# convert to np.float32
Z = np.float32(Z)

# define criteria, number of clusters(K) and apply kmeans()
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 10, 1.0)
K = 7
ret,label,center=cv2.kmeans(Z,K,None,criteria,10,cv2.KMEANS_RANDOM_CENTERS)

# Now convert back into uint8, and make original image
center = np.uint8(center)
res = center[label.flatten()]
res2 = res.reshape((img.shape))

cv2.imshow('res2',res2)
cv2.waitKey(0)
cv2.destroyAllWindows()

이미지를 7개의 색상만으로 구성되도록 양자화하는 것으로 결과는 다음과 같습니다.