최단 경로 탐색 알고리즘 중 A*(A Star, 에이 스타) 알고리즘에 대해 실제 예시를 통해 풀어가면서 설명하겠습니다. A* 알고리즘은 시작 노드만을 지정해 다른 모든 노드에 대한 최단 경로를 파악하는 다익스트라 알고리즘과 다르게 시작 노드와 목적지 노드를 분명하게 지정해 이 두 노드 간의 최단 경로를 파악할 수 있습니다.
A* 알고리즘은 휴리스틱 추정값을 통해 알고리즘을 개선할 수 있는데요. 이러한 휴리스틱 추정값을 어떤 방식으로 제공하느냐에 따라 얼마나 빨리 최단 경로를 파악할 수 있느냐가 결정됩니다.
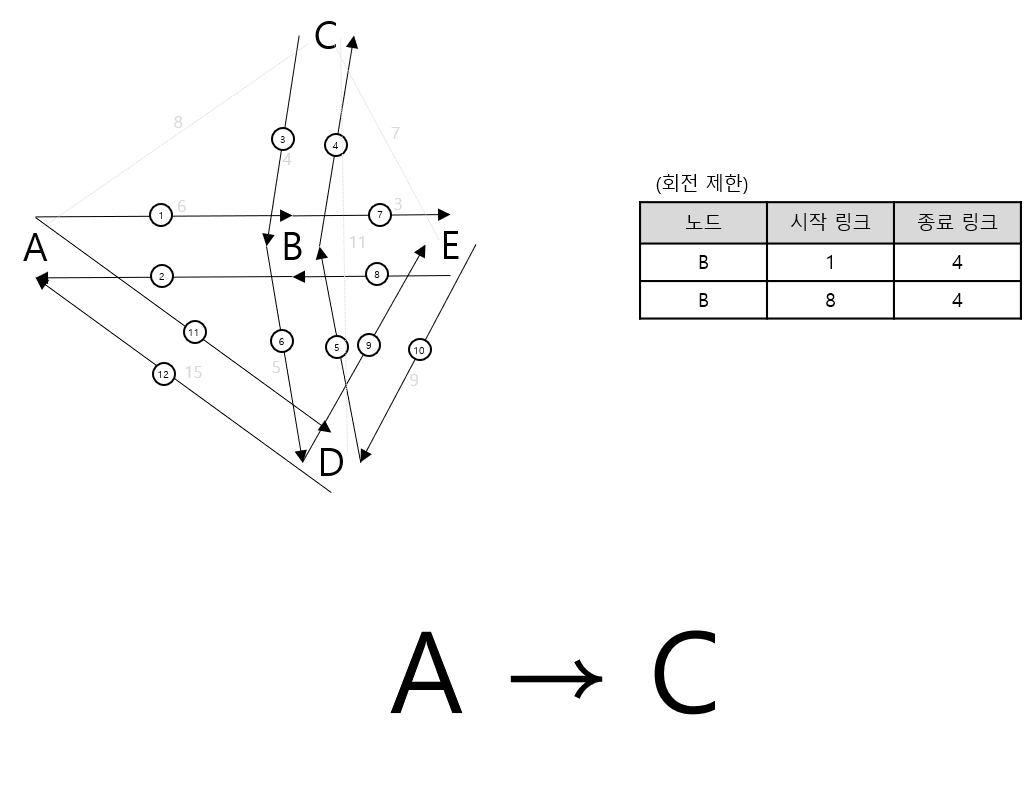
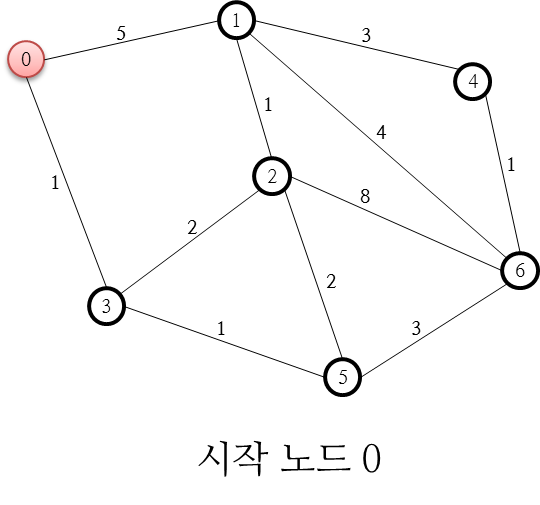
A*에 대한 서론은 최대한 배제하고 하나의 명확한 예를 통해 풀어나가며 설명하도록 하겠습니다. 다음과 같은 예를 통해 먼저 살펴보겠습니다.
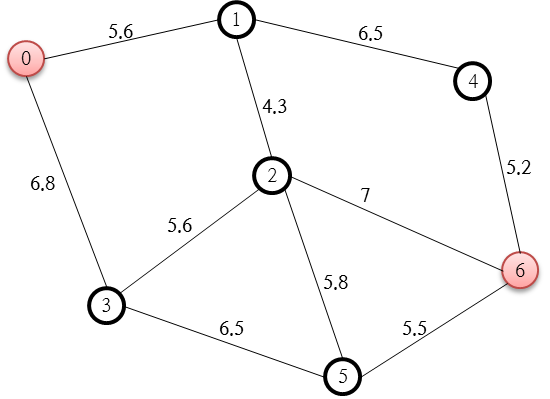
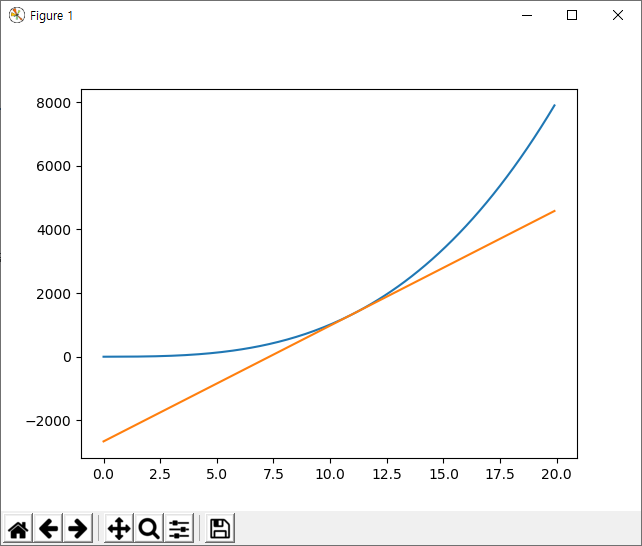
위의 예는 시작점인 0번 노드에서 목적지인 6번 노드로 가는 최단 경로를 A* 알고리즘으로 분석하고자 하는 것인데요. 각 노드 사이에 연결된 링크에 붙은 숫자는 노드 사이를 이동하는데 소요되는 비용(경비, Cost)입니다. 위의 경우 거리값입니다. 즉, 노드 사이의 거리가 길수록 비용이 늘어나므로 비용값으로써 합리적입니다.
A* 알고리즘을 통한 위의 문제 해결을 위해 가장 먼저 수행하는 첫 과정은 다음과 같습니다.
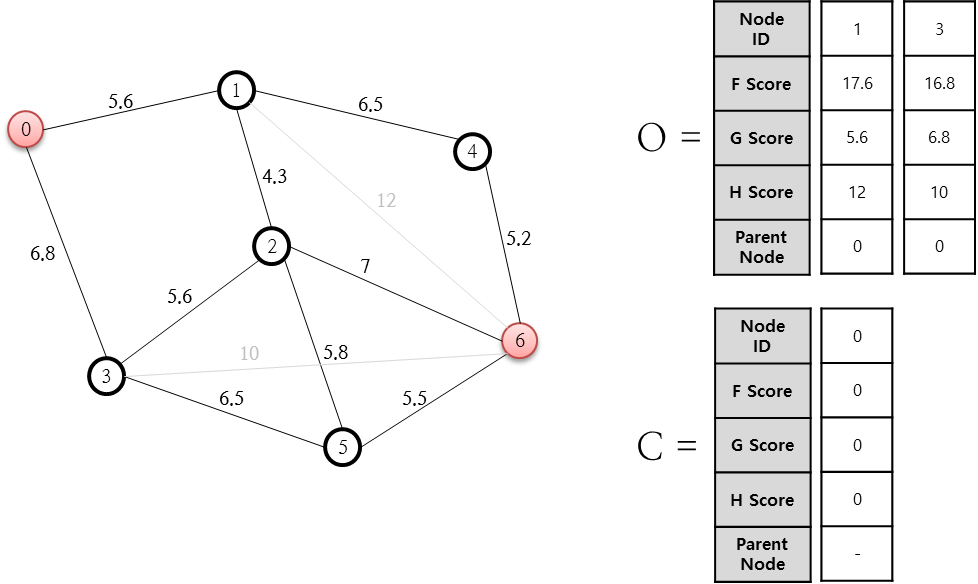
위의 그림에서 보면 저장소로 O와 C가 있는데요. O는 열린 목록(Open List), C는 닫힌 목록(Close List)인데요. 열린 목록인 O 저장소에는 최단 경로를 분석하기 위한 상태값들이 계속 갱신되며, C 저장소는 처리가 완료된 노드를 담아 두기 위한 목적으로 사용됩니다. 이러한 O와 C의 저장소를 기반으로 0번 노드에서 6번 노드까지의 최단 경로를 산출해 보도록 하겠습니다.
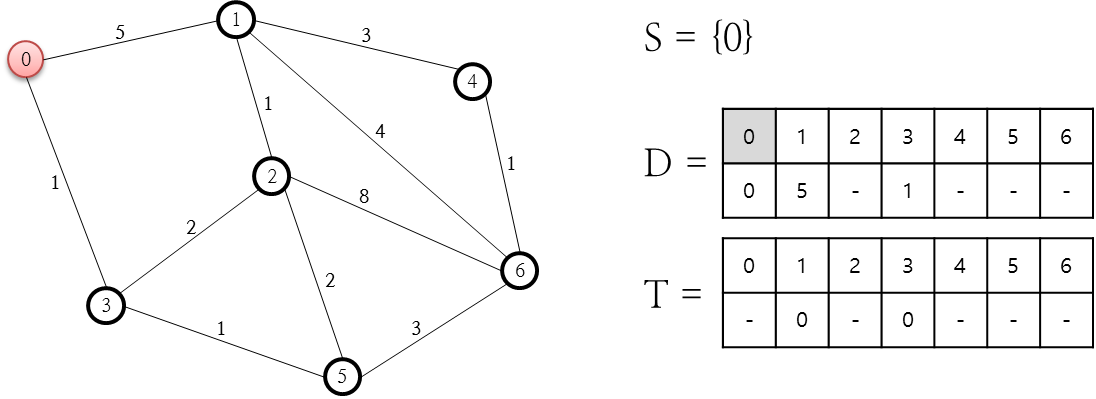
먼저 출발 노드인 0을 닫힌 목록인 C 목록에 집어 넣습니다. 그리고 이 0번 노드와 연결된 노드는 1번과 3번 노드를 열린 목록인 O 저장소에 추가합니다. 추가할 때 F, G, H, Parent Node값도 함게 추가해야 하는데요. 먼저 F = G + H입니다. G는 시작 노드에서 해당 노드까지의 실제 소요 경비값이고, H는 휴리스틱 추정값으로 해당 노드에서 최종 목적지까지 도달하는데 소요될 것이라고 추정되는 값입니다. Parent Node는 해당 노드에 도달하기 직전에 거치는 노드 번호입니다. 먼저 1번 노드에 대한 F, G, H, Parent Node를 살펴 보겠습니다. 출발점인 0번 노드로부터 시작했으므로, 1번 노드의 Parent Node는 0번 노드입니다. 그리고 G 값은 0번 노드에서 1번 노드까지의 거리 비용값인 5.6입니다. H 값을 추정하기 위한 기준이 필요한데요. 이 추정값에 대한 기준을 1번 노드에서 목적지인 6번 노드까지의 직선 거리로 하기로 정하고 측정을 하니(줄자로 재든, 좌표가 있다면 피타고라스 정리를 통해 두 좌표 사이의 거리를 계산하든 하여 얻을 수 있음) 12로 산출되므로 H는 12가 됩니다. F = G + H이므로 5.6 + 12인 17.6이 됩니다. 3번에 대한 F, G, H, Parent Node 역시 이와 동일하게 결정할 수 있습니다. 여기서 다음 단계로 진행합니다.
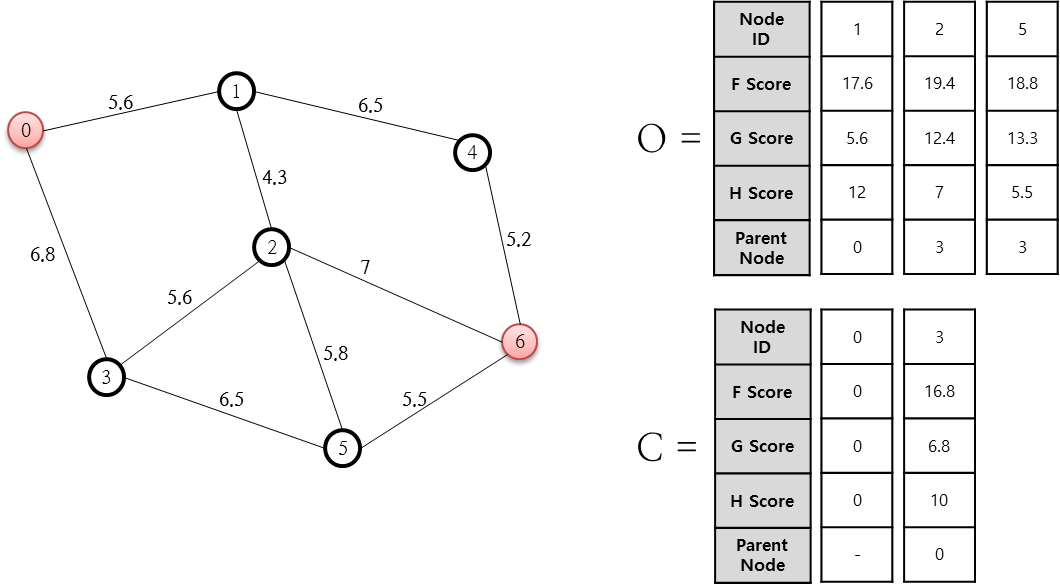
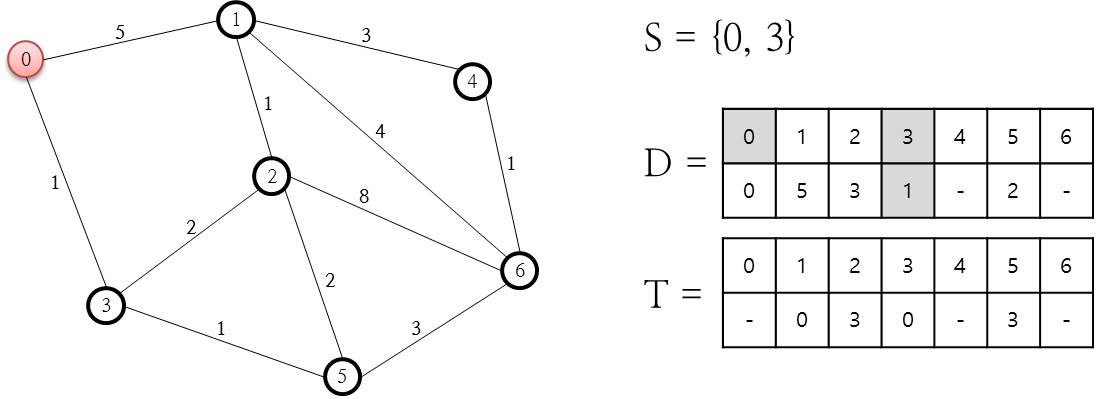
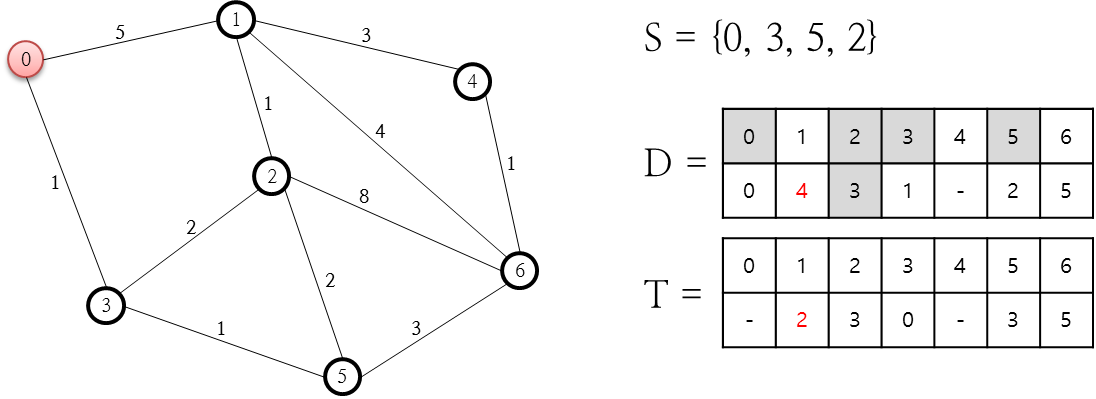
O 리스트 중 F 값이 가장 작은 노드는 3번인데요. 이 노드 3번을 C 리스트에 추가하고 3번 노드와 연결된 0, 2, 5 중 닫힌 목록에 존재하지 않는 2, 5번 노드에 대해 열린 목록에 추가합니다. 2, 5에 대한 F, G, H, Parent Node를 계산해 기록합니다. 먼저 2번 노드에 대해 계산해 보면.. 2번 노드에 대한 G 값은 바로 직전 노드에 소요되는 비용(6.8)에 3번 노드에서 2번 노드까지 도달하기 위한 비용인 5.6을 합한 값인 12.4가 됩니다. 그리고 H 값은 2번 노드에서 목적지은 6번까지에 대한 거리값인 7이 됩니다. 5번 노드에 대한 것도 이와 동일하게 계산합니다. 다음으로 진행합니다.
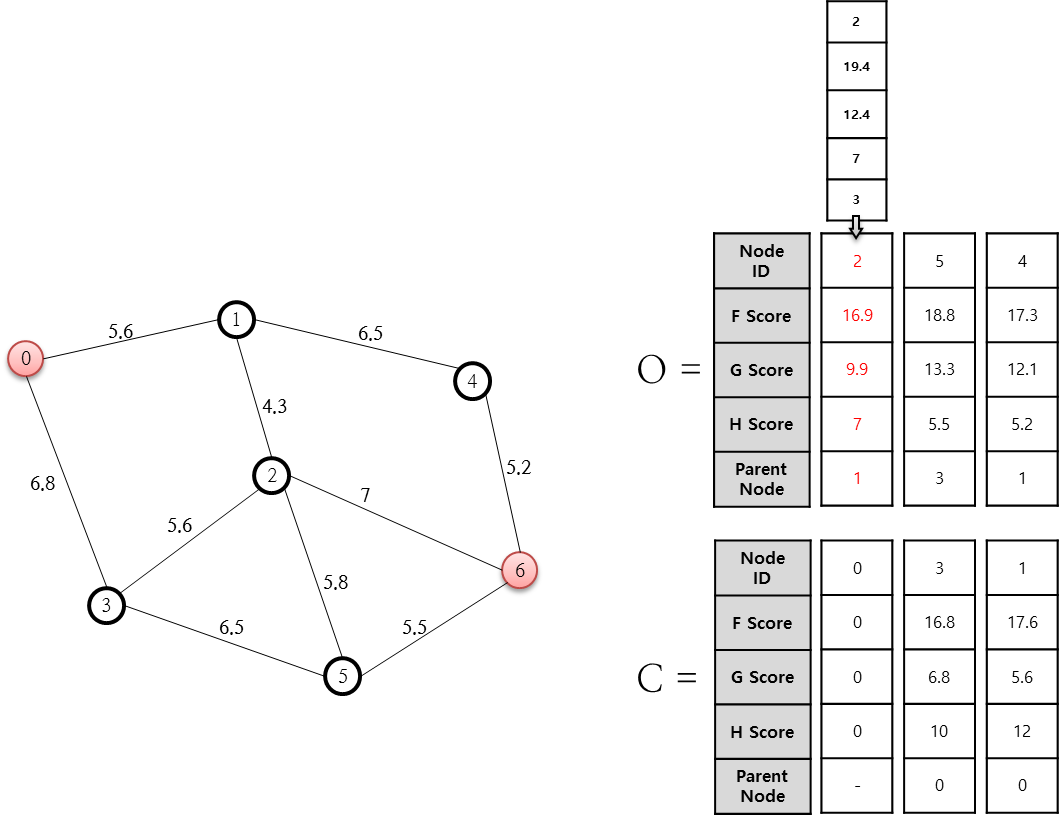
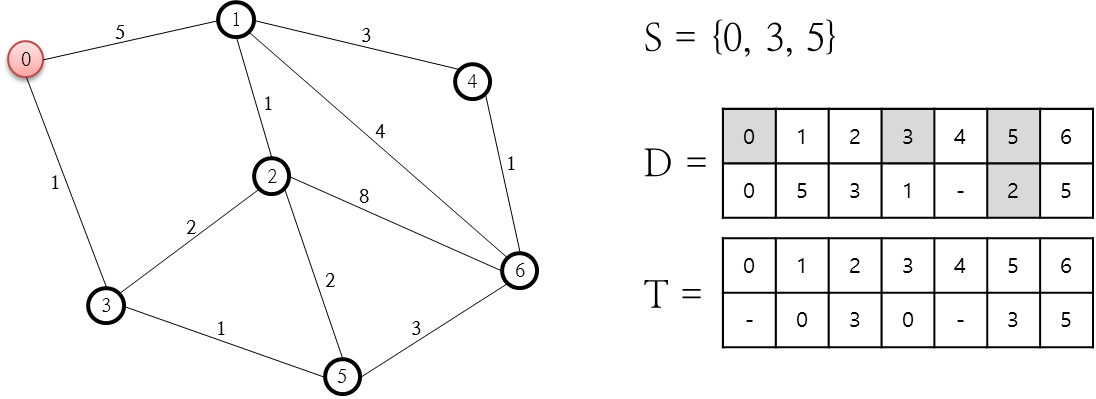
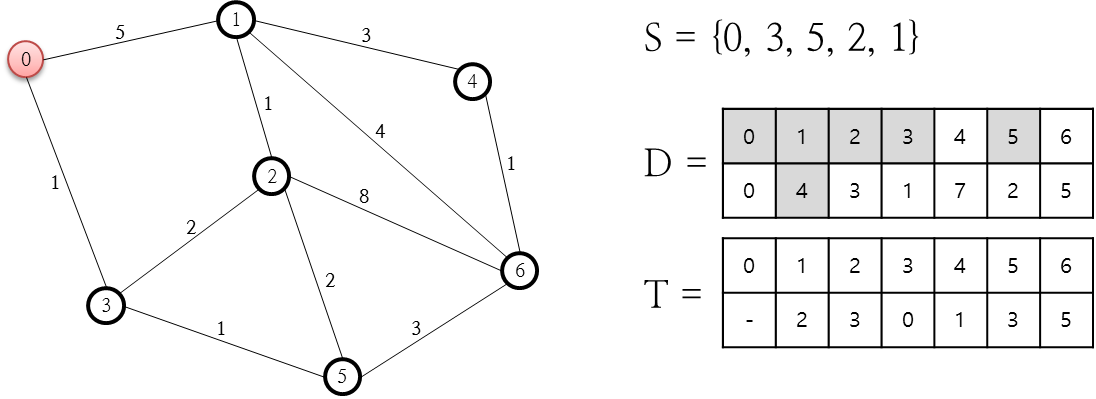
열린 목록(O 저장소) 중 F 값이 가장 작은(최소인) 1번 노드를 닫힌 목록에 추가합니다. 그리고 이 1번 노드와 연결된 2, 4번 노드 중 닫힌 목록(C 저장소)에 존재하지 않는 것에 대해 다시 F, G, H, Parent Node를 계산합니다. 이 상태에서 4번 노드는 열린 목록에 없었던 것이기에 그냥 F, G, H, Parent Node를 이미 앞서 설명했던 방식으로 계산해 추가하면 그만이지만 2번 노드는 전 단계에서 이미 추가되어 있었는데요. 이렇게 전 단계에서 추가된 G 값이 새롭게 계산된 G 값보다 크다면 새롭게 계산된 F, G, H, Parent Node 값으로 변경해 줘야 하며 위의 그림이 이러한 변경을 나타내고 있습니다. 다음 단계로 진행합니다.
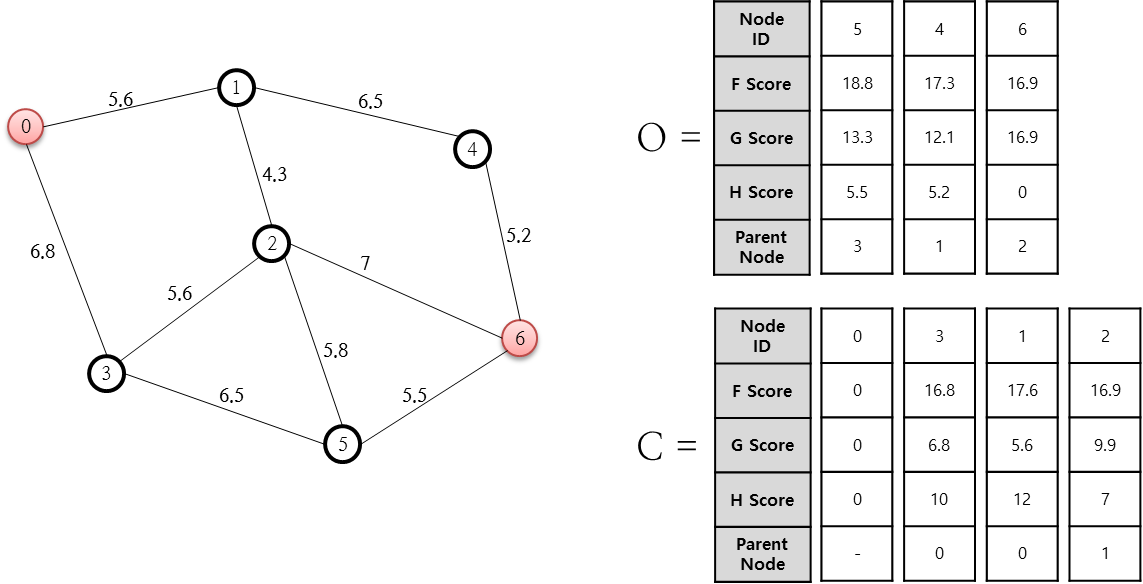
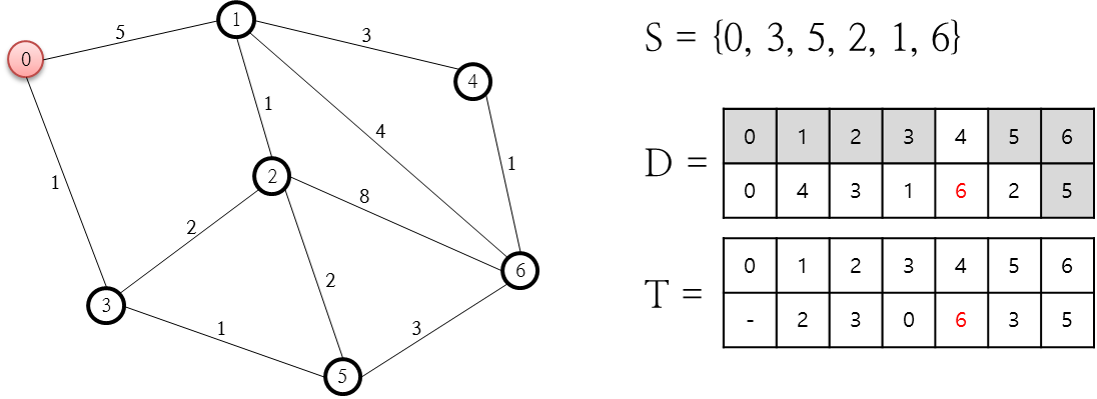
열린 목록 중 F가 최소인 노드는 2번 노드이고, 이 2번 노드를 닫힌 목록에 추가합니다. 그리고 2번 노드와 연결된 1, 3, 5, 6번 노드 중 닫힌 목록에 존재하지 않는 5, 6번 노드에 대한 F, G, H Parent Node 값을 계산합니다. 5번 노드의 경우 새로운 G 값이 기존 값보다 크므로 변경하지 않고 6번 노드에 대한 값들만을 계산해 추가합니다. 다음 단계로 진행합니다.
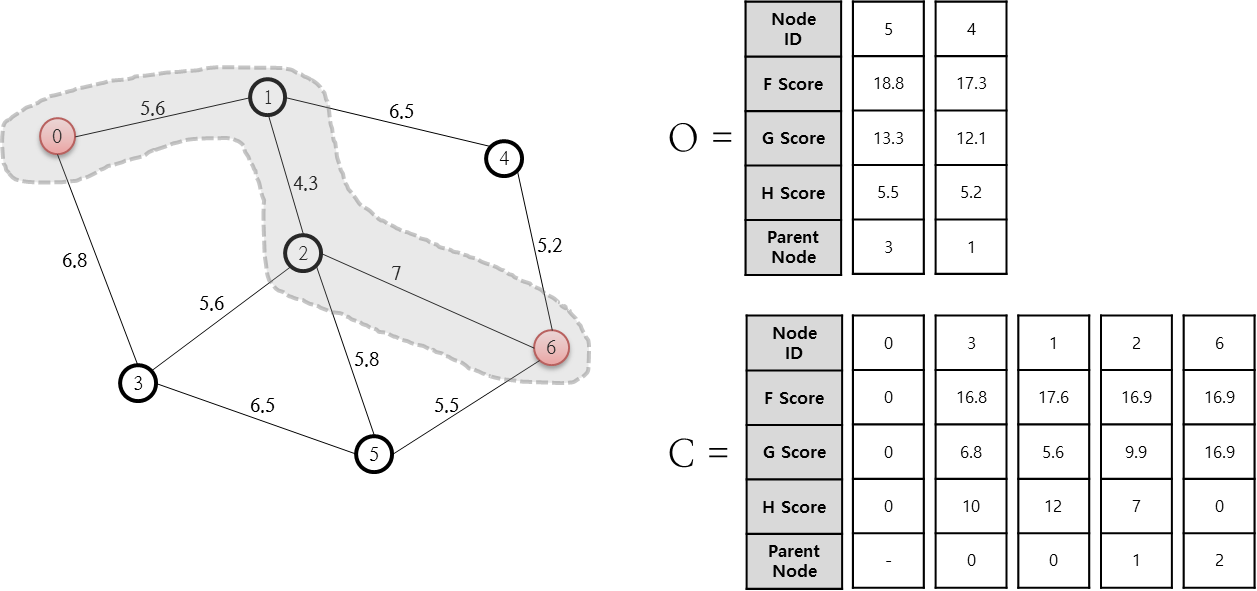
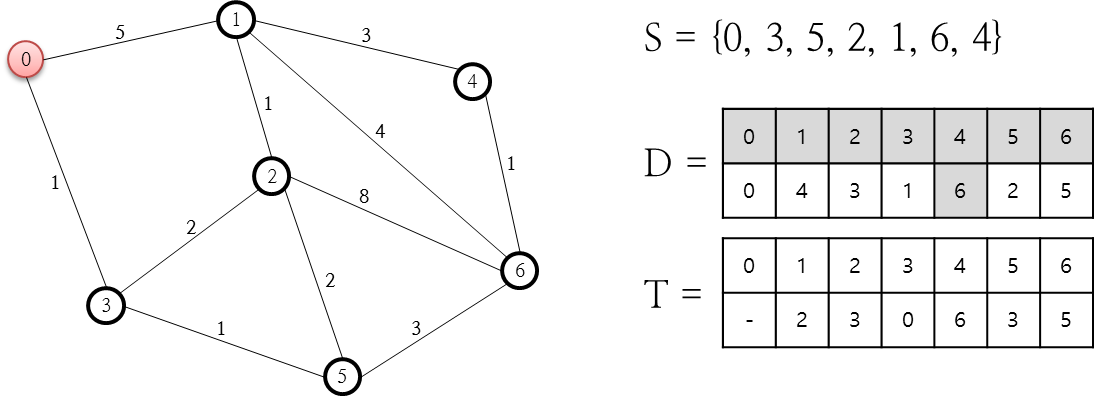
열린 목록 중 F가 최소인 노드는 6번 노드인데요. 이 6번 노드를 닫힌 목록에 추가합니다. 그런데 이 6번 노드는 최종 목적지 노드이므로 A* 알고리즘은 종료됩니다.
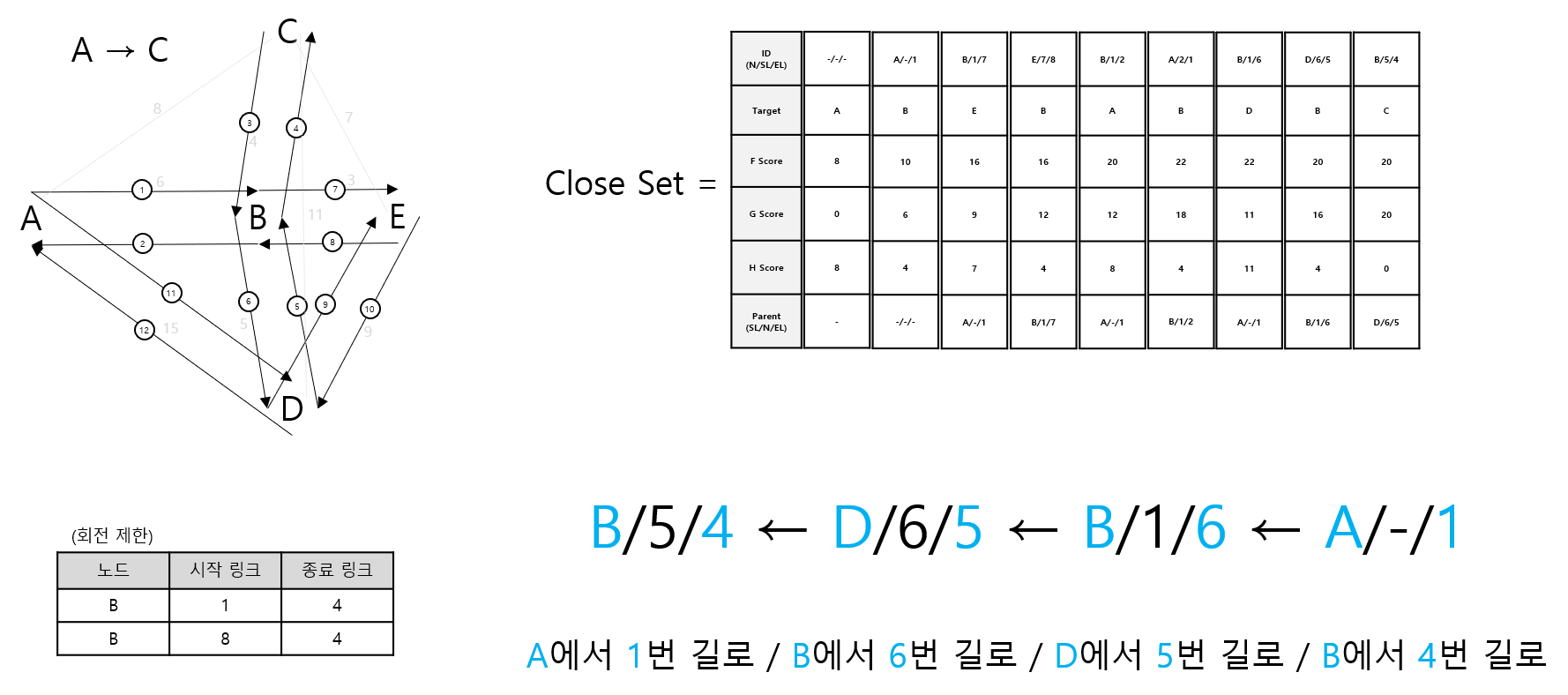
여기까지 만들어진 닫힌 목록(C 저장소)를 토대로 0번 노드에서 6번 노드까지의 최단 경로를 파악할 수 있습니다. 6번 노드의 Parent Node는 2번 이고, 2번 노드의 Parent Node는 1번이며, 1번 노드의 Parent Node는 0번이므로 최단 경로는 6번 노드←2번 노드←1번 노드←0번 노드가 됩니다.