[카테고리:] OpenCV

이 글의 원문은 https://opencv-python-tutroals.readthedocs.io/en/latest/py_tutorials/py_objdetect/py_face_detection/py_face_detection.html 입니다.

Haar 특징기반 다단계 분류자(Feature-based Cascade Classifiers)를 이용한 물체 검출은 Paul Viola와 Michael Jones이 2001년에 발표한 논문, “Rapid Object Detection using a Boosted Cascade of Simple Features”에서 제안된 효과적인 물체 검출 방법입니다. 이는 검출할 대상이 되는 물체가 있는 이미지와 없는 이미지(각각을 Positive Image와 Negative Image라고 함)을 최대한 많이 활용해서 다단계 함수를 훈련시키는 기계학습 방식입니다.

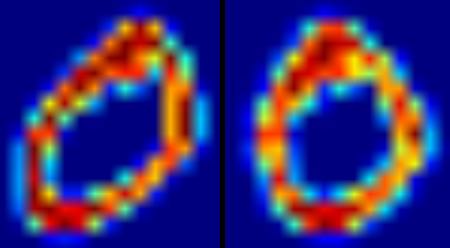
이 글에서는 검출할 대상을 얼굴로 시험해 봅니다. 처음에, 이 알고리즘은 분류자(Classifier)를 훈련시키기 위해 매우 많은 훈련용 이미지가 필요합니다. 이 이미지는 앞서 언급한 Positive와 Negative 이미지입니다. 다음 단계는 특징들(Features)를 추출해야 합니다. 이를 위해, 아래 그림에서의 Haar 특징이 사용됩니다. 이는 마치 컨볼루션 커널(Convolutional Kernel)과 같습니다. 각 특징은 하얀색 사각형에서의 픽셀값의 합을 검정색 사각형 영역의 픽셀값의 합에서 뺀 값입니다.

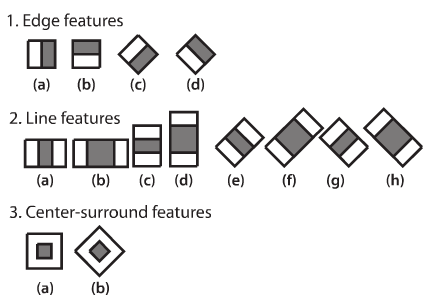
많은 특징을 계산하기 위해 이미지에 적용할 각 커널에 대한 모든 가능한 크기와 위치를 고려해야 합니다. 얼마나 많은 계산이 필요할까요? 24×24 크기의 이미지만 해도 160000개 이상의 특징 결과값이 존재합니다. 각 특징을 계산하기 위해서, 하얀색 영역과 검정색 영역의 픽셀의 합을 얻어야 합니다. 이를 위해, 논문에서는 인테그랄(Integral) 이미지를 언급합니다. 이 이미지는 픽셀의 합의 계산을 단순화 시켜 줍니다. 이는 알고리즘 속도를 매우 빠르게 개선시켜 줍니다.

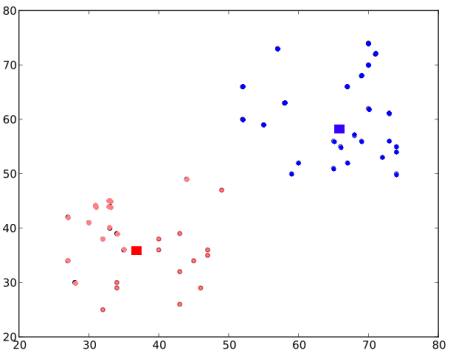
그러나 이렇게 계산된 모든 특징들 중 대부분이 적합하지 않습니다. 예를들어, 아래의 이미지를 봅시다. 첫번째 선택된 특징은 눈 영역이 코나 뺨 영역보다 자주 어둡다라는 점에 주목합니다. 두번째 선택된 특징은 눈이 미간보다 어둡다는 것에 주목합니다. 그러나 뺨이나 다른 곳에 적용된 동일한 이미지는 부적절합니다. 그래서 160000개 이상의 특징 중 최고의 특징을 어떻게 선택해야 할 것인가가 문제입니다. 이 문제를 Adaboost가 해결해 냈습니다.

이를 위해서, 모든 훈련 이미지들에 대해 각각의 모든 특징을 적용합니다. 각 특징에 대해, 이미지 상에 얼굴이 있는지 없는지(즉 positive 또는 negative 인지)를 분류될 최고의 임계값을 찾습니다. 그러나 명백하게, 여기에는 오류와 잘못된 분류가 존재합니다. 최소한의 에러율로 특징을 선택하는데, 이는 얼굴 이미지인지, 얼굴이 아닌 이미지인지를 아주 잘 분류한다는 것을 의미합니다. (이런 처리는 말처럼 간단하지 않습니다. 각 이미지는 시작부터 동일한 가중치가 주어집니다. 각각의 분류 후에, 잘못 분류된 이미지의 가중치는 증가합니다. 그러면 다시 같은 절차가 수행됩니다. 새로운 에러율이 얻어지거나 원하는 개수의 특징점이 발견됩니다.)

최종 분류자는 이러한 약한 분류자 들의 가중치 합입니다. 약하다고 하는 이유는 분류자 하나만으로 이미지를 분류하지 못하고 분류자들이 모여야만 제대로 이미지를 분류할 수 있기 때문입니다. 논문에서는 200개의 특징만으로도 90%의 정확도를 제공한다고 합니다. 최종적으로 약 6000개의 특징점이 도출됩니다. (160000개 이상의 특징점이 6000개의 특징점으로 줄었다는 것은 엄청난 이득입니다.)

이제 이미지를 취합니다. 각 24×24 크기의 윈도우를 잡습니다. 6000개의 특징을 이미지에 적용합니다. 얼굴이 있는지 없는지 검사합니다. 그런데, 이 방식은 시간 소모도 많고 비효율적입니다. 논문의 저자는 이를 위해 좋은 해결책을 제시합니다.

이미지에서, 이미지 영역의 대부분은 얼굴이 아닌 영역입니다. 이 생각은 윈도우가 얼굴 영역이 아닌지를 검사하는 간단한 방법이 됩니다. 만약 얼굴 영역이 아니라면, 이를 단번에 버립니다. 다시 수행하지 않습니다. 대신 얼굴이 있는 곳의 영역에 초점을 맞춥니다.

이를 위해 논문의 저자들은 다단계 분류자(Cascade of Classifiers)의 개념을 소개합니다. 윈도우에 대한 6000개의 모든 특징을 적용하는 대신, 분류자의 다른 단계로 특징을 묶고 하나씩 하나씩 적용하는 것입니다. (보통 처음 몇몇 단계는 매우 적은 수의 특징을 갖습니다.) 만약 윈도우가 첫번째 단계에서 실패하면 버립니다. 나머지 특징들은 더 이상 고려하지 않습니다. 만약 통과되면 특징의 두번째 단계를 정용하고 이를 계속 반복합니다. 모든 단계를 통과한 윈도우가 얼굴 영역이 됩니다!!

이제 이 Haar Cascades 알고리즘을 구현한 OpenCV의 함수를 이용해 얼굴을 검출해 보는 코드를 살펴 보겠습니다.

OpenCV는 트레이너와 검출자 모드를 제공합니다. 차량이나 비행기와 같은 물체 검출을 위한 자신만의 훈련이 필요하다면 OpneCV를 이용해 훈련시킬 수 있습니다. (참조 : https://docs.opencv.org/2.4/doc/user_guide/ug_traincascade.html)

이 글에서는 검출에 대해서만 설명합니다. OpenCV에서는 이미 얼굴, 눈 등에 대한 미리 훈련된 데이터를 XML 파일 형식으로 제공합니다. 바로 이 XML 분류자 파일을 로드 하는 것이 시작입니다. 그리고 분류할 이미지를 Grayscale로 로드하는 것입니다.

import numpy as np
import cv2
from matplotlib import pyplot as plt

face_cascade = cv2.CascadeClassifier('./data/haar/haarcascade_frontface.xml')
eye_cascade = cv2.CascadeClassifier('./data/haar/haarcascade_eye.xml')

img = cv2.imread('./data/haar/img.jpg')
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

다음은 입력 이미지에서 얼굴을 검출하는 것입니다. 만약 얼굴을 발견하면, 발견한 얼굴에 대한 위치를 Rect(x,y,w,h) 형태로 얻을 수 있습니다. 이 위치를 얻었다면, 얼굴에 대한 ROI를 만들고, 이 안에서 눈을 검출합니다. (눈은 얼굴 안에 있으니까요!)

faces = face_cascade.detectMultiScale(gray, 1.3, 5)

for (x,y,w,h) in faces:
    cv2.rectangle(img,(x,y),(x+w,y+h),(255,0,0),2)
    roi_gray = gray[y:y+h, x:x+w]
    roi_color = img[y:y+h, x:x+w]
    eyes = eye_cascade.detectMultiScale(roi_gray)
    for (ex,ey,ew,eh) in eyes:
        cv2.rectangle(roi_color,(ex,ey),(ex+ew,ey+eh),(0,255,0),2)

cv2.imshow('img',img)
cv2.waitKey(0)
cv2.destroyAllWindows()

실행 결과는 다음과 같습니다.

아이언맨의 얼굴과 캡틴아메리카의 얼굴은 검출되지 못했는데, 이는 훈련 데이터가 정면에서 본 얼굴에 대한 이미지들로 만들어졌기 때문입니다.

이 글의 원문은 https://opencv-python-tutroals.readthedocs.io/en/latest/py_tutorials/py_photo/py_non_local_means/py_non_local_means.html 입니다.

이 글에서는 이미지 안의 잡음을 제거하기 위해 Non-local Means 잡음제거 알고리즘에 대해 살펴봅니다. 이를 위한 OpenCV에서 제공하는 cv2.fastNlMeansDenoising(), cv2.fastNlMeansDenoisingColored() 등과 같은 함수들의 차이점에 대해서도 살펴봅니다.

이전 글에서, 가우시안 블러링, 메디안 블러링 등과 같은 이미지를 부드럽게 만드는 기법에 대해 살펴 보았으며, 이런 연산이 어느 정도의 잡음을 제거할 수 있었음을 보였습니다. 이들 방식은, 픽셀 주위의 다른 픽셀들 몇개를 취해 값들의 평균값등으로 원래의 값을 변경합니다. 요약하면, 이런 방식의 잡음 제거는 자신의 이웃에 한해서만 이루어집니다.

잡음에는 어떤 성질이 있습니다. 잡음은 일반적으로 제로 평균(Zero Mean)을 가진 무작위로 생겨납니다. 잡음 픽셀, 을 살펴봅시다. 는 픽셀의 참 값이고 은 그 픽셀의 잡음입니다. 다른 이미지들에서 동일한 픽셀들을(이라 합시다) 많이 취해서, 이들의 평균을 계산합니다. 이상적으로는 잡음의 평균은 0이므로 이여야 합니다.

간단한 설정을 통해 이것을 확인할 수 있습니다. 고정 카메라를 어떤 위치에 몇초간 놓습니다. 그러면 동일한 장면에 대한 많은 이미지 또는 프레임을 얻을 수 있겠죠. 그러고는 찍힌 모든 프레임의 평균을 구하는 코드를 작성합니다. 첫번째 프레임과 최종 결과를 비교해 봅시다. 잡음이 감소된 것을 볼 수 있을 것입니다. 불행히도 이 간단한 방법은 카메라와 움직이는 장면에 대해서는 적용하기 어렵습니다.

아이디어는 간단한데, 비슷한 이미지에 대한 잡음의 평균값들이 필요합니다. 이미지에서 작은 윈도우(5×5 크기로 합시다)를 고려해 봅시다. 하나의 이미지 안에는 동일한 조각이 다른 위치 여러 곳에 존재할 가능성이 큽니다. 때때로 조각 근처에 나타날 수 있습니다. 이러한 유사한 조각들을 활용해서 이들의 평균을 구한다면 어떨까요? 아래의 그림을 봅시다.

이미지에서 파란색 조각들은 유사해 보입니다. 파란색 조각도 유사해 보이죠. 이러한 픽셀을 취해, 이 픽셀 주위에 작은 윈도우를 만들어, 이미지에서 유사한 윈도우 영역을 찾아서, 모든 윈도우들의 평균을 내고, 그 평균 결과로 픽셀을 교체합니다. 이 방법이 NonLocal Means Denosing(잡음제거)이라고 합니다. 앞서 봤던 블러링(Burring) 기법과 비교하면 시간은 더 소요되지만, 결과는 매우 좋습니다.

칼라 이미지에 대해서, 이미지를 CIELAB 칼라공간(Colorspace)로 변경하고 L과 AB 요소에 대해 별도로 잡음을 제거 합니다.

이런 방법에 대해서 OpenCV에서는 4가지 방식을 제공합니다.

1. cv2.fastNlMeansDenoising() – 그레이 이미지 하나에 대해서만 작동함
2. cv2.fastNlMeansDenoisingColored() – 칼라 이미지 하나에 대해서 작동함
3. cv2.fastNlMeansDenoisingMulti() – 짧은 시간 동안 찍힌 여러 개의 이미지에 대해서 작동하며 그레이 이미지여야 함
4. cv2.fastNlMeansDenoisingColoredMulti() – 짧은 시간 동안 찍한 여러 개의 이미지에 대해서 작동하며 칼라 이미지에서 작동함

위 함수들의 공통 인자는 다음과 같습니다.

• h : 필터 강도를 결정하는 인자. 더 높은 h 값이 잡음을 더 잘 제거하지만 잡음이 아닌 픽셀도 제거함(10이면 적당함)
• hForColorComponents : h와 동일하지만, 칼라 이미지에 대해서만 사용됨(보통 h와 같음)
• templateWindowSize : 홀수값이여야 함(7을 권장함)
• searchWindowSize : 홀수값이여야 함(21을 권장함)

이 글에서는 2번과 3번에 대한 예제를 살펴 봅니다.

1. cv2.fastNlMeansDenoisingColored()

앞서 언급했듯이 칼라 이미지로부터 잡음을 제거 하는데 사용됩니다. 코드는 아래와 같습니다.

import numpy as np
import cv2
from matplotlib import pyplot as plt

img = cv2.imread('./data/die.png')

dst = cv2.fastNlMeansDenoisingColored(img,None,10,10,7,21)

plt.subplot(121),plt.imshow(img)
plt.subplot(122),plt.imshow(dst)
plt.show()

아래는 결과인데, 입력 이미지는 인 가우시안 잡음을 가지고 있습니다.

2. cv2.fastNlMeansDenoisingMulti()

이제 비디오에 대해서도 동일한 방법을 적용해 봅시다. 첫번째 인자는 잡음이 들어간 프레임 리스트입니다. 두번재 인자 imgToDenoiseIndex는 잡음을 제거할 프레임의 인덱스인데, 이를 위해 입력 리스트에 프레임 인덱스를 전달합니다. 세번째 인자는 temporalWindowSize으로 잡음 제거를 위해 사용할 인근 프레임의 개수입니다. 이 값은 홀수여야 합니다. 예제는 다음과 같습니다.

import numpy as np
import cv2
from matplotlib import pyplot as plt

cap = cv2.VideoCapture('./data/TownCentreXVID.mp4')

# create a list of first 5 frames
img = [cap.read()[1] for i in range(5)]

# convert all to grayscale
gray = [cv2.cvtColor(i, cv2.COLOR_BGR2GRAY) for i in img]

# convert all to float64
gray = [np.float64(i) for i in gray]

# create a noise of variance 25
noise = np.random.randn(*gray[1].shape)*10

# Add this noise to images
noisy = [i+noise for i in gray]

# Convert back to uint8
noisy = [np.uint8(np.clip(i,0,255)) for i in noisy]

# Denoise 3rd frame considering all the 5 frames
dst = cv2.fastNlMeansDenoisingMulti(noisy, 2, 5, None, 4, 7, 35)

plt.subplot(131),plt.imshow(gray[2],'gray')
plt.subplot(132),plt.imshow(noisy[2],'gray')
plt.subplot(133),plt.imshow(dst,'gray')
plt.show()

결과는 다음과 같습니다.

계산에 소요되는 시간이 상당한데, 첫번째 이미지는 원본 프레임이고 두번째는 잡음을 넣은 것이며 마지막은 두번째 이미지에 대한 잡음을 제거한 것입니다.

이 글의 원문은 https://opencv-python-tutroals.readthedocs.io/en/latest/py_tutorials/py_ml/py_kmeans/py_kmeans_opencv/py_kmeans_opencv.html 입니다.

OpenCV에서 K-Means 알고리즘을 이용한 데이터 군집화는 cv2.kmeans() 함수를 통해 이용 됩니다. 이 함수에 대한 인자는 다음과 같습니다.

1. samples : np.float32 데이타 타입이며, 각 피쳐(Feature)는 단일 열(Column)으로 저장되어져 있어야 합니다.
2. nclusters(K) : 군집화할 개수
3. criteria : 반복을 종료할 조건입니다. 조건이 만족되면 알고리즘의 반복은 중지됩니다. 3개의 인자를 갖는 튜플(Tuple)이며, (type, max_iter, epsilon)입니다. 각각의 대한 인자는 다음과 같습니다.
   • type : 종료 조건의 타입으로 cv2.TERM_CRITERIA_EPS는 주어진 정확도(epsilon 인자)에 도달하면 반복을 중단하고, cv2.TERM_CRITERIA_MAX_ITER는 max_iter 인자에 지정된 횟수만큼 반복하고 중단합니다. cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER를 조합해 사용하면 두가지 조건 중 하나가 만족되면 반복이 중단됩니다.
   • max_iter : 최대 반복할 횟수(정수형 타입)
   • epsilon : 정확도
4. attempts : 다른 초기 라벨링을 사용하면서 실행되는 알고리즘의 실행 횟수를 지정하는 플래그. 알고리즘은 최적의 컴팩트함(Compactness)을 만드는 라벨을 반환합니다. 이 컴팩트함은 출력으로 반환됩니다.
5. flags : 초기값을 잡을 중심에 대한 플래그로써 cv2.KMEANS_PP_CENTERS와 cv2.KMEANS_RANDOM_CENTERS 중 하나가 사용됩니다.

이 함수의 반환값은 다음과 같습니다.

1. compactness : 각 포인트와 군집화를 위한 중심 간의 거리의 제곱의 합
2. labes : 라벨에 대한 배열이며, ‘0’, ‘1’ 같이 이전 글에서 언급한 내용과 같음.
3. centers : 클러스터의 중심이 저장된 배열

이제 3가지 예를 통해 K-Means 알고리즘이 어떻게 OpenCV에서 사용되는지 살펴봅시다.

1. 하나의 특징(Feature)을 가지는 데이터

오직 하나의 특징을 가지는 데이터, 예를 들어 1차원 데이터 셋을 봅시다. 그러니까 T셔츠의 크기를 결정하기 위해 사람의 키에 대한 특징만을 고려하는 것입니다.

데이터를 생성하고 Matplotlib으로 표시해 보면..

import numpy as np
import cv2
from matplotlib import pyplot as plt

x = np.random.randint(25,100,25) 
y = np.random.randint(175,255,25)
z = np.hstack((x,y))
z = z.reshape((50,1))
z = np.float32(z)
plt.hist(z,256,[0,256]),plt.show()

크기 50개의 배열 z가 있으며, 구성 요소의 값은 0~255 사이입니다. z를 단일 열(column)로 구성합니다. 마지막으로 데이터의 타입을 np.float32로 변환합니다. 결과는 다음과 같습니다.

이제, K-Means 함수를 적용해 봅시다. 알고리즘 종료에 대한 기준 조건을 정해야 합니다. 여기서 기준은 10반 반복과 정확도(epsilon)은 1.0으로 정합니다.

# Define criteria = ( type, max_iter = 10 , epsilon = 1.0 )
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 10, 1.0)

# Set flags (Just to avoid line break in the code)
flags = cv2.KMEANS_RANDOM_CENTERS

# Apply KMeans
compactness,labels,centers = cv2.kmeans(z,2,None,criteria,10,flags)

위 예제의 cv2.kmeans 함수는 compactness와 labels, centers 변수에 반환값을 넘겨줍니다. 이 경우 centers는 57.92과 114.5이며, labels에는 각 요소에 대해 ‘0’, ‘1’ 중에 하나의 값으로 분류된 라벨값입니다. 여기서 이 라벨값을 기반으로 데이터를 A와 B 변수로 나눠봅시다.

A = z[labels==0]
B = z[labels==1]

그리고 A와 B를 각각 파란색과 빨간색으로 표시하고, 군집화된 중심을 노란색으로 표시해 봅시다.

# Now plot 'A' in red, 'B' in blue, 'centers' in yellow
plt.hist(A,256,[0,256],color = 'r')
plt.hist(B,256,[0,256],color = 'b')
plt.hist(centers,32,[0,256],color = 'y')
plt.show()

결과는 아래와 같습니다.

2. 여러 개의 특징(Feature)을 가지는 데이터

이전 예에서, T셔츠에 대해 오직 키에 대한 특징점만을 고려했습니다. 여기서는 키와 몸무게처럼 2개의 특징점을 고려해 봅시다.

이전 경우에서, 입력 데이터를 단일 열(column) 벡터로 구성했다는 것을 기억해야 합니다. 각 특징은 열로 정렬되어 잇어야 합니다. 예를 들어서, 이 경우 50명의 사람에 대해 키와 몸무게 값으로 구성된 50×2 크기의 테스트 데이터를 구성합니다. 첫번째 열(Column)은 50명에 대한 키 값이고 두번째 열은 이들의 키값입니다. 첫번째 행(Row)는 첫번째 사람의 키와 몸무게 값입니다. 즉, 아래 그림과 같은 구성입니다.

바로 코드를 보면..

import numpy as np
import cv2
from matplotlib import pyplot as plt

X = np.random.randint(25,50,(25,2))
Y = np.random.randint(60,85,(25,2))
Z = np.vstack((X,Y))

# convert to np.float32
Z = np.float32(Z)

# define criteria and apply kmeans()
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 10, 1.0)
ret,label,center=cv2.kmeans(Z,2,None,criteria,10,cv2.KMEANS_RANDOM_CENTERS)

# Now separate the data, Note the flatten()
A = Z[label.ravel()==0]
B = Z[label.ravel()==1]

# Plot the data
plt.scatter(A[:,0],A[:,1])
plt.scatter(B[:,0],B[:,1],c = 'r')
plt.scatter(center[:,0],center[:,1],s = 80,c = 'y', marker = 's')
plt.xlabel('Height'),plt.ylabel('Weight')
plt.show()

결과는 다음과 같습니다.

3. 색상 양자화(Color Quantization)

색상 양자화는 이미지에서 사용하는 색상의 수를 줄이는 처리입니다. 이러한 처리를 하는 목적 중 하나는 사용하는 메모리를 줄이기 위해서입니다. 색상 양자화를 위해 K-Means 클러스터링을 활용해 보겠습니다.

새롭게 추가되는 새로운 내용은 없습니다. 특징점은 3개인데, 바로 R, G, B입니다. 이미지의 화소 데이터를 Mx3 배열로 만다는데, M은 이미지의 화소 개수입니다. 클러스터링 이후에, 중심점(이 값 역시도 R, G, B 임)값으로 해당 소속되는 화소의 값을 변경합니다. 그리고 다시 Mx3 배열을 원래 이미지의 크기로 재구성하면 됩니다. 코드는 다음과 같습니다.

import numpy as np
import cv2

img = cv2.imread('./data/harleyQuinnA.jpg')
Z = img.reshape((-1,3))

# convert to np.float32
Z = np.float32(Z)

# define criteria, number of clusters(K) and apply kmeans()
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 10, 1.0)
K = 7
ret,label,center=cv2.kmeans(Z,K,None,criteria,10,cv2.KMEANS_RANDOM_CENTERS)

# Now convert back into uint8, and make original image
center = np.uint8(center)
res = center[label.flatten()]
res2 = res.reshape((img.shape))

cv2.imshow('res2',res2)
cv2.waitKey(0)
cv2.destroyAllWindows()

이미지를 7개의 색상만으로 구성되도록 양자화하는 것으로 결과는 다음과 같습니다.

이 글의 원문은 https://opencv-python-tutroals.readthedocs.io/en/latest/py_tutorials/py_ml/py_kmeans/py_kmeans_understanding/py_kmeans_understanding.html 입니다.

이 글은 K-Means 클러스터링에 대한 개념을 예를 통해 설명합니다.

티셔츠를 만다는 어떤 회사가 있다고 합시다. 이 회사는 새로운 티셔츠를 만들어 시장에 뿌리려고 합니다. 분명이 이 회사는 모든 사람들이 만족하는 다양한 티셔츠 사이즈를 생산해야 합니다. 그래서 이 회사는 사람들의 키와 몸무게의 데이터를 수집해서 아래처럼 그래프로 표현 했습니다.

회사는 모든 사이즈에 대한 티셔츠를 만들 수는 없습니다. 대신에 작은 사이즈, 중간 사이즈, 큰 사이즈와 같이 3가지 사이즈를 만들고 모든 사람이 이 셋 중에 하나를 골라 만족하기를 기대합니다. 사람들을 이 3개의 그룹으로 나누는 것은 K-Means 클러스터링을 통해 가능하며, 이 알고리즘은 모든 사람들이 만족할 수 있는 최적의 3가지 사이즈를 산출해 낼 것입니다. 3가지로 부족하다면 4개로 그룹을 나눌 것이고.. 계속 만족할 만한 개수의 그룹으로 늘려나갈 수 있습니다. 아래 그럼처럼요.

자, 이제 이 K-Means 클러스터링의 알고리즘을 알아 봅시다. 그림을 통해 단계별로 설명하겠습니다.

아래와 같은 데이터셋을 살펴봅시다. 이 데이터셋을 앞서 언급한 티셔츠 데이터라고 할 수 있습니다. 이 데이터를 2개의 그룹으로 군집화(Clustering)해 봅시다.

1단계

무작위로 2개의 중심점을 선택합니다. 이 중심점은 C1과 C2라고 합시다. (그냥 데이터 셋중 2개를 잡아서 그 2개가 C1, C2라고 해도 됩니다)

2단계

데이터셋을 구성하는 각각의 모든 포인트와 C1, C2 사이의 거리를 계산합니다. 만약 해당 포인트(테스트 데이터)가 C1에 더 가깝다면, 그 포인트에 ‘0’이라는 라벨을 붙입니다. 만약 C2에 더 가깝다면 ‘1’이라는 라벨을 붙이구요. (더 많은 중심점이 있다면 ‘2’, ‘3’ 등등이 되겠죠) 우리의 경우, ‘0’ 라벨은 빨간색으로, ‘1’ 라벨은 파란색으로 표시했습니다. 이 단계를 통해 아래와 같은 이미지를 얻을 수 있습니다.

3단계

파란색 포인트 전체와 빨간색 포인트 전체에 대한 각각의 평균을 계산하고 이 평균을 새로운 중심점으로 갱신합니다. 즉 C1과 C2는 새롭게 계산된 중심점으로 이동되겠죠. 그리고 2단계를 다시 수행합니다. 그럼 다음과 같은 결과가 얻어집니다.

2단계와 3단계를 반복하는데, 중심점 C1과 C2가 더 이상 변경되지 않을 때까지 반복합니다. (또는 반복 회수의 제한을 두던지.. 중심점의 변경시 이동 거리에 대한 기준 등을 만족할때까지 반복할 수도 있습니다.) 반복이 멈추게 되면, 중심점과 이들 중심점과 연관된 포인트 간의 거리의 합이 최소가 됩니다. 간단이 말해, 와 사이의 거리합이 최소입니다.

최종 결과는 아래와 같게 됩니다.

바로 이것이 K-Means 클러스터링에 대한 직관적인 이해이며, K-Means의 최상위 개념입니다. 여기에 다양한 변종과 응용이 추가됩니다. 예를들어 초기 중심점을 어떻게 결정하여 알고리즘의 속도를 향상시킬까 하는 등의 고민이 필요합니다.