[카테고리:] Python

작성일자

Python 가상환경 만들고 VS.Code에서 사용하기

가상환경 생성하고 VS.Code에서 원하는 가상환경을 선택하도록 하는 과정을 정리해 둡니다.

일단 콘설창을 실행하고, 생성하고자 하는 가상환경 가상환경이 저장될 폴더로 이동한 뒤 아래의 명령을 입력합니다.

python -m venv python_virtualenv

그러면 python_virtualenv 폴더가 생성된 것을 확인할 수 있습니다. 여기까지가 파이선에서 가상환경 생성의 전부입니다.

이제 VS.Code에서 이 가성환경을 통해 코드를 실행하기 위한 설정입니다.

VS.Code를 실행하고 단축키 F1를 누르면 Python에 대한 인터프리터를 선택할 수 있는 항목이 표시됩니다. 이 항목을 클릭합니다.

“+ 인터프리터 경로 입력…”을 클릭하고 “찾기…”에서 이전에 생성한 가상환경 폴더에 위치한 Scripts/python.exe 파일을 선택합니다.

이제 새로운 터미널이 표시될때마다 다음처럼 가상환경 이름 표시와 함께 명령 프롬프트가 표시됩니다.

그리고 GDAL 설치는 다음과 같습니다.

먼저 WHL 파일을 다운로드(https://www.lfd.uci.edu/~gohlke/pythonlibs/#gdal) 받고 다음 명령으로 설치하면 됩니다.

pip install .\GDAL-3.4.3-cp311-cp311-win_amd64.whl
작성일자

matplotlib에서 애니메이션 그래프 표현하기

matplotlib는 다양한 그래프를 표현할 수 있는데요. 정적인 그래프 뿐만 아니라 데이터가 실시간으로 변경되면 그에 대한 동적인 그래프도 표현할 수 있습니다. 아래는 예시로써 그 결과입니다.

위의 예시를 실제로 구현하기 위한 코드를 살펴 보겠습니다. 이를 위해 먼저 그래프로 표현하기 위한 데이터가 필요한데, 아래의 코드는 데이터를 구성하는 코드입니다.

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation

data = np.random.uniform(0, 1, (64, 75))
X = np.linspace(-1, 1, data.shape[-1])
G = 1.5 * np.exp(-4 * X ** 2)

예시의 결과를 보면, 65개의 꺽은선 그래프로 구성되어 있습니다. 아래는 이 꺽은선 그래프를 구성하는 코드입니다.

import matplotlib.pyplot as plt

fig = plt.figure(figsize=(8, 8))
ax = plt.subplot(111, frameon=False)

lines = []
for i in range(data.shape[0]):
    xscale = 1 - i / 200.0
    lw = 1 - i / 100.0
    line, = ax.plot(xscale * X, i + G * data[i], color="k", lw=lw)
    lines.append(line)

이제 최종적으로 데이터를 0.2초마다 변경하고, 변경된 데이터에 대한 그래프를 업데이트하면서 마치 동적으로 그래프가 움직이는 효과를 내는 코드를 살펴 보겠습니다.

import matplotlib.animation as animation

ax.set_xticks([])
ax.set_yticks([])

ax.text(0.5, 1.0, "MATPLOTLIB ", transform=ax.transAxes, ha="right", va="bottom", color="k", 
        family="sans-serif", fontweight="bold", fontsize=16)
ax.text(0.5, 1.0, "DYNAMIC", transform=ax.transAxes, ha="left", va="bottom", color="k",
        family="sans-serif", fontweight="light", fontsize=20)

def update(*args):
    data[:, 1:] = data[:, :-1]
    data[:, 0] = np.random.uniform(0, 1, len(data))

    for i in range(len(data)):
        lines[i].set_ydata(i + G * data[i])

anim = animation.FuncAnimation(fig, update, interval=200)
plt.show()
작성일자

단순 선형 회귀에 대한 2가지 접근

잡음이 섞인 샘플 데이터가 선형이라고 가정할때, 이 선형 모델은 기울기와 절편이라는 값으로 정의됩니다. 이 기울기와 절펀에 대한 값을 구하는 방법은 다양한데, 이 글에서는 2가지 접근 방법을 언급합니다. 먼저 잡음이 섞인 샘플 데이터는 다음과 같습니다.

import numpy as np
import matplotlib.pyplot as plt

X = 10 * np.random.rand(100,1)
y = 3.7 - 2.5 * X + np.random.randn(100,1)
plt.scatter(X, y)
plt.show()

위의 코드는 샘플 데이터에 대한 시각화 코드도 포함하고 있는데, 그 결과는 다음과 같습니다.

이제 위의 샘플 데이터에 대한 선형회귀 방법 중 하나인 정규방정식(Normal Equation)에 대한 코드는 다음과 같습니다.

X_b = np.c_[np.ones((100,1)), X]
w = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
print(w)

plt.scatter(X, y)
drawLine(w[1], w[0])
plt.show()

분석된 절편과 기울기에 대한 출력 및 결과 모델의 선형은 다음과 같습니다.

[[ 3.76686801]
 [-2.50677558]]

아울러 정규방정식은 다음과 같습니다.

    $$(X^{T}X)^{-1}X^{T}y$$

다음은 사이킷런에서 제공하는 LinearRegression 클래스를 이용한 방법입니다.

from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X, y)
w = [model.intercept_[0], model.coef_[0][0]]
print(w)

plt.scatter(X, y)
drawLine(w[1], w[0])
plt.show()

분석된 절편과 기울기에 대한 출력 및 결과 모델의 선형은 다음과 같습니다.

[[ 3.69686801]
 [-2.50677558]]

위의 코드에서 절편과 기울기를 통해 그래프를 그리는 함수인 drawLine은 다음과 같습니다.

def drawLine(m, b):
    X = np.arange(0, 11)
    y = [m * x + b for x in X]
    plt.plot(X, y)
작성일자

혼돈행렬(Confusion Matrix)와 정밀도, 재현률, F1점수

이 글은 한빛미디어의 핸즈온 머신러닝을 수업자료로써 파악하면서 이해한 바를 짧게 요약한 글입니다. 요즘 이 책을 통해 머신러닝을 다시 접하고 있는데, 체계적이고 좋은 내용을 제공하고 있고, 나 자신을 위한 보다 명확한 이해를 돕고자 이 글을 작성 작성합니다. 요즘 제가 블로그에 올리는 머신러닝 관련 글은 대부분 이 책의 내용에 대한 나름대로의 해석을 토대로 합니다. 보다 자세한 내용은 해당 도서를 참고하기 바랍니다.

이글은 훈련된 예측 모델을 평가하기 위한 지표인 정밀도, 재현률, F1에 대한 내용입니다. 이러한 평가 지표는 혼돈행렬이라는 데이터를 토대로 계산되는데요, 먼저 혼돈행렬을 구하기 위해 학습 데이터셋이 필요하며, 0~9까지의 숫자를 손으로 작성한 MINIST를 사용하고, 이 손글씨가 7인지에 대한 예측 모델을 예로 합니다. MNIST 데이터셋을 다운로드 받고, 레이블 데이터를 재가공합니다.

from sklearn.datasets import fetch_openml
import numpy as np

mnist = fetch_openml('mnist_784', version=1, data_home='D:/__Temp__/_')

X, y = mnist["data"], mnist["target"]
y = y.astype(np.uint8)

X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
y_train_7 = (y_train == 7)
y_test_7 = (y_test == 7)

예측 모델은 SGDClassifier를 사용합니다.

from sklearn.linear_model import SGDClassifier

model = SGDClassifier(random_state=3224)

혼돈 행렬을 얻기 위해 다음 코드를 실행합니다.

from sklearn.model_selection import cross_val_predict
from sklearn.metrics import confusion_matrix

y_train_pred = cross_val_predict(model, X_train, y_train_7, cv=3)
cf = confusion_matrix(y_train_7, y_train_pred)
print(cf)

[[53223   512]
 [  726  5539]]

cross_val_predict 함수는 아직 전혀 학습이 되지 않은 모델을 지정된 교차검증 수만큼 학습시킨 뒤 예측값을 반환합니다. 이렇게 얻은 예측값과 실제 값을 비교해서 얻은 혼돈행렬의 결과에 대한 상세한 이미지는 아래와 같습니다.

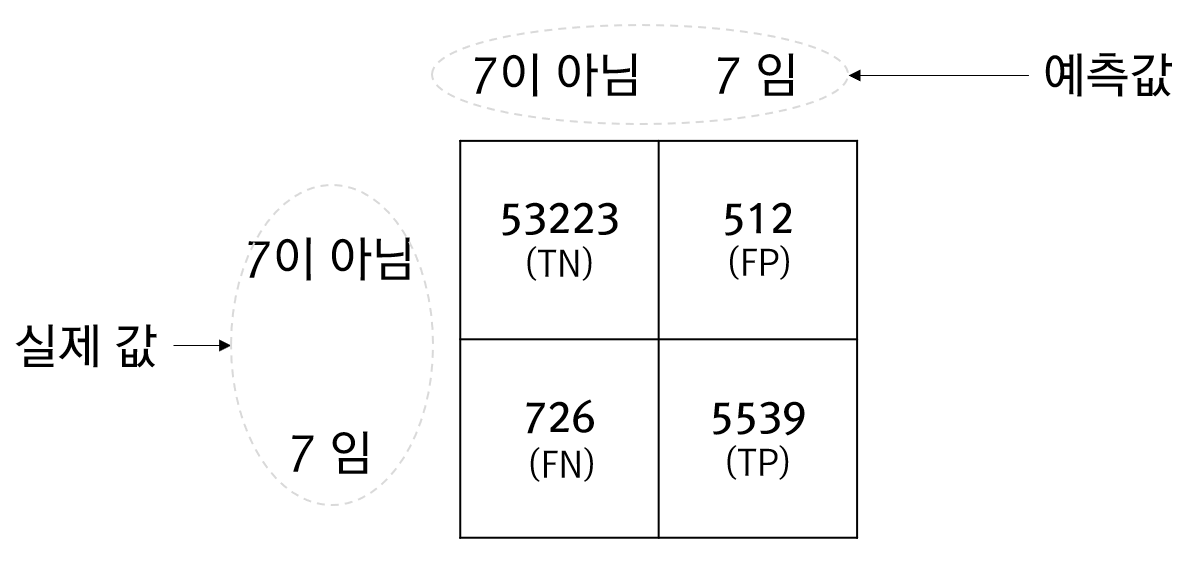
위의 그림에서 표에 담긴 4개의 값은 발생횟수입니다. TN과 TP의 값은 옳바르게 예측한 횟수이고 FN과 FP는 잘못 예측한 횟수입니다. 즉, FN과 FP가 0일때 모델은 완벽하다는 의미입니다.

이제 위의 혼돈행렬에서 정밀도(Precision)와 재현률(Recall), F1점수에 대한 수식은 다음과 같습니다.

    $$Precision=\frac{TP}{TP+FP}, Recall=\frac{TP}{TP+FN},F1=2\times\frac{Precision \times Recall}{Precision+Recall}$$

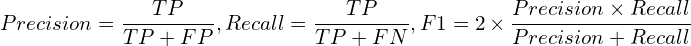
정밀도와 재현률이 서로 상반관계에 있습니다. 즉, 정밀도가 높으면 재현률이 떨어지며 재현률이 높아지면 정밀도가 떨어지는 경향이 있습니다. F1은 이런 상반관계에 있는 정밀도와 재현률을 묶어 평가하고자 하는 지표입니다.

비록 정밀도와 재현률, F1점수는 매우 단순해 계산하기 쉬우나 다음의 코드를 통해서도 쉽게 얻을 수 있습니다.

from sklearn.metrics import precision_score, recall_score, f1_score
p = precision_score(y_train_7, y_train_pred)
print(p)
r = recall_score(y_train_7, y_train_pred)
print(r)
f1 = f1_score(y_train_7, y_train_pred)
print(f1)

0.9153858866303091
0.8841181165203511
0.8994803507632347