TensorFlow2를 이용한 간단한 회귀분석

TensorFlow v2가 정식버전으로 배포된지 몇달이 지났습니다. 필자는 딥러닝 라이브러리로 PyTorch를 주력으로 하고 있으나, TensorFlow로 만들어진 많은 코드 분석 및 협업을 위해 TensorFlow에 대한 API도 관심이 많습니다. 이 글에서는 TensorFlow 버전2에서 sin 함수에 대한 회귀분석에 대한 샘플 코드를 설명합니다.

필요한 패키지에 대한 import 및 훈련 데이터와 테스트 데이터를 아래 코드를 통해 준비합니다.

import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import SGD, RMSprop, Adam
from tensorflow.keras import metrics

np.random.seed(0)

train_x = np.linspace(0,np.pi*2,10).reshape(10,1)
train_y = np.sin(train_x)
test_x = np.linspace(0,np.pi*2,100).reshape(100,1)
test_y = np.sin(test_x)

sin 함수에 대한 회귀분석을 위한 신경망 모델은 다음과 같습니다.

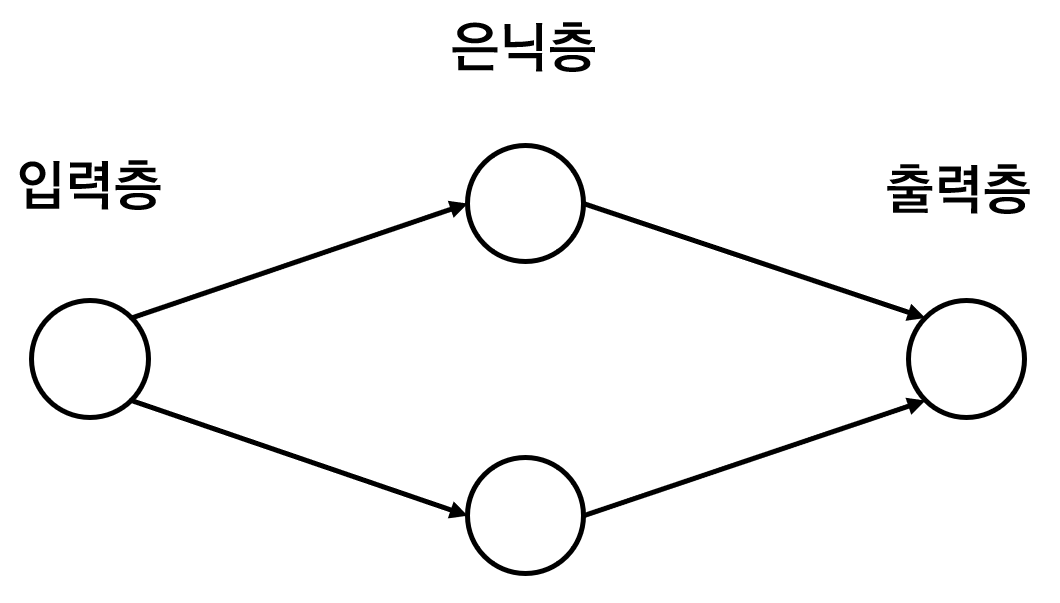
sin 함수는 1개의 입력값을 받아 1개의 출력값을 가지므로 입력층과 출력층의 뉴런 개수는 1개입니다. 중간의 은닉층의 뉴런은 임의로 2개로 잡았습니다. 이 신경망 모델을 구성하는 코드는 다음과 같습니다.

input_nodes = 1
hidden_nodes = 2
output_nodes = 1

model = Sequential()

model.add(Dense(hidden_nodes, input_dim=input_nodes, activation='sigmoid'))
model.add(Dense(output_nodes))

print(model.summary())

모델 상세 정보가 콘솔에 표시되는데, 다음과 같습니다.

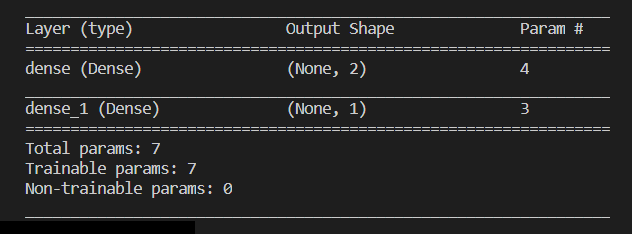
파라메터의 개수는 가중치 w 뿐만 아니라 편차값인 b 값도 고려해야 합니다.

신경망을 학습할 것인데, 학습에 사용할 최적화 방식으로 4가지를 사용합니다. 아래 코드에 사용할 최적화 방법에 대한 구체적인 코드는 다음과 같습니다.

optimizers = {
    'SGD': SGD(lr=0.1),
    'Momentum': SGD(lr=0.1, momentum=0.9), 
    'RMSProp': RMSprop(lr=0.01),
    'Adam': Adam(lr=0.01)
}

다음 코드는 학습입니다.

train_results = []
train_y_predicted = []
test_y_predicted = []

for optimizer_name, optimizer in optimizers.items():
    print(optimizer_name, 'Training ...')

    model.compile(optimizer=optimizer, loss='mean_squared_error', metrics=['mse'])

    result = model.fit(train_x, train_y, epochs=1000, verbose=0)
    train_results.append(result)

    train_result = model.predict(train_x)    
    train_y_predicted.append(train_result)

    test_result = model.predict(test_x)
    test_y_predicted.append(test_result)

위의 코드 중 8번의 model.compile은 모델 학습하기 위해 먼저 호출해야 하는 코드입니다. 인자로 loss와 metrics가 있는데, 각각 가질 수 있는 값은 ‘mean_squared_error'(주로 회귀용), ‘categorilcal_crossentropy'(주로 다중분류), binary_crossentropy'(주로 이진분류) 등과 ‘mse'(주로 회귀용), ‘accuracy'(주로 분류용) 등입니다. 그리고 실제 학습은 10번 코드를 통해 이뤄집니다. 단 1줄로 말입니다. 이 부분은 케라스의 장점이죠. model.fit 함수의 결과값은 손실값과 정확도에 대한 값을 포함합니다. 13번 코드와 16번 코드는 훈련된 모델을 통해 실제 계산을 수행하는 코드입니다. 각각 학습 데이터와 테스트 데이터로 계산을 수행해 그 결과를 배열에 담습니다.

앞의 코드에서는 중간 결과를 배열에 담았는데요. 이렇게 담은 배열은 최종 결과 그래프를 생성하기 위해 다음처럼 사용됩니다.

fig, axes = plt.subplots(3,1)
axes[0].plot(train_x, train_y, '-o', label = 'sin(x)')
for i, optimizer_name in enumerate(optimizers.keys()):
    axes[0].plot(train_x, train_y_predicted[i], '--', label=optimizer_name)
axes[0].legend()    

axes[1].plot(test_x, test_y, '-o', label = 'sin(x)')
for i, optimizer_name in enumerate(optimizers.keys()):
    axes[1].plot(test_x, test_y_predicted[i], '--', label=optimizer_name)
axes[1].legend()

for i, optimizer_name in enumerate(optimizers.keys()):
    axes[2].plot(train_results[i].history['loss'], '--', label=optimizer_name)
axes[2].legend()

plt.show()

결과는 다음과 같습니다.

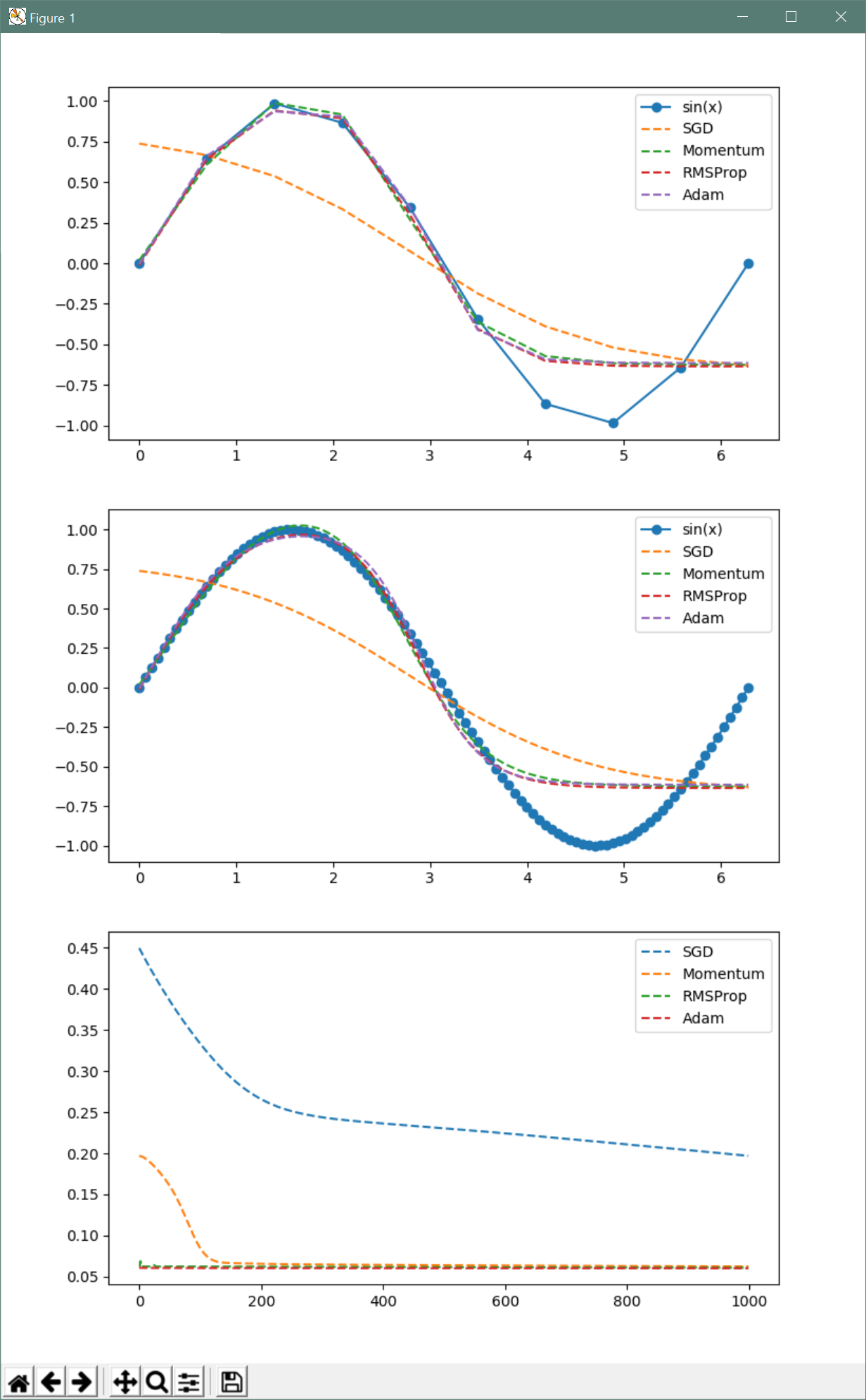
이 경우 Momentum와 RMSprop의 장점을 섞은 Adam 최적화 방식이 가장 좋은 결과를 제공하는 것을 알 수 있습니다.