몬테카를로 방법(Montecarlo Method)

몬테카를로 방법(Monte Carlo method)은 어떤 문제에 대한 해를 무수히 많은 시도를 통해 얻어진 확률을 기반으로 하는 계산법입니다. 아래의 그림은 위키디피아의 몬테카를로에 대한 소개에 나온 이미지로써 원주율 π 값을 구하는 예입니다.

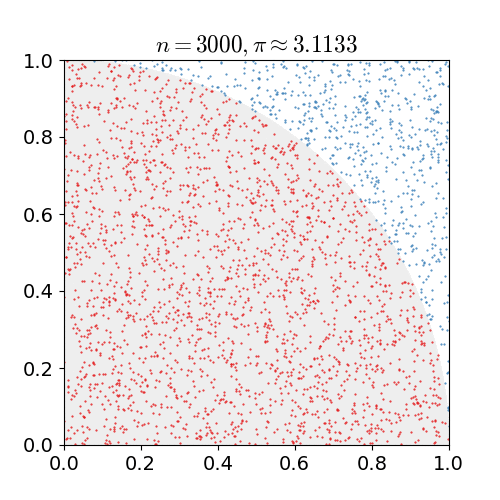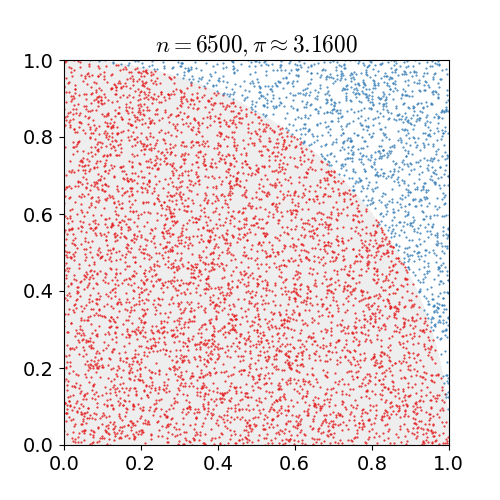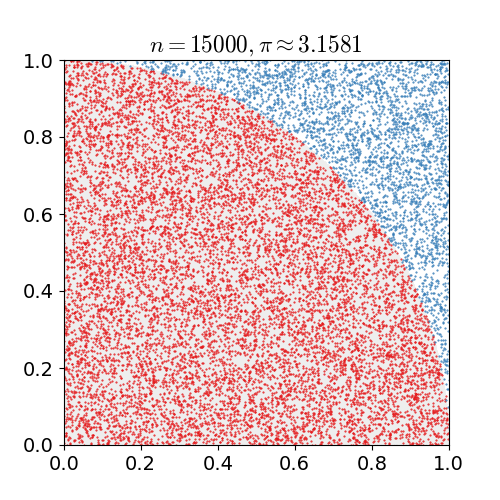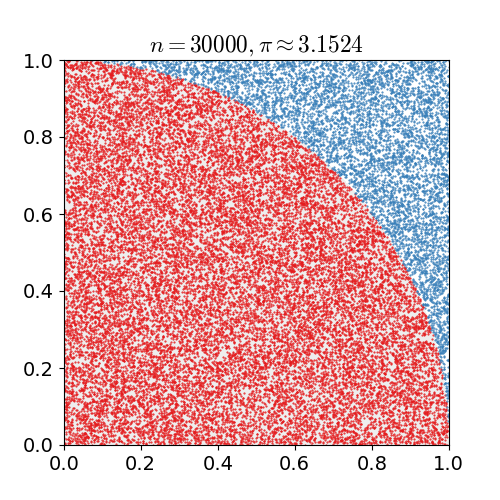
넓이가 1인 정사각형, 이 정사각형 내부에 반지름이 1인 사분원이 있습니다. 그러면 사분원이 차지하는 넓이는 π/4가 될 것이다. 이제 0 이상, 1 이하인 x와 y의 값을 무작위로 뽑은 후 x^2 + y^2 ≤ 1의 조건을 만족할 확률은 사분원의 넓이와 같은 π/4가 됩니다.

위의 논리를 코드로 작성하여 π를 구하면 다음과 같습니다.

import random

n = 1000000 # 백만번의 시도
count = 0

for i in range(n):
    # x, y를 무작위로 0~1사이의 값으로 결정
    x = random.uniform(0, 1)
    y = random.uniform(0, 1)

    # 사분원 내부에 발생하는 경우수 
    if (x**2 + y**2) <= 1: count += 1

# 백만번의 시도 중 사분원 내부일 경우에 대한 확률은 사분원의 넓이이므로 이를 4배 곱하여 π 계산
print('phi', 4*count/n)

위의 코드 중 4*count/n은 다음의 비례식을 통해 도출된 결과입니다.

전체확률 : 사분원 내부일 경우에 대한 확률 = 사각형의 넓이 : 사분원의 넓이

위의 비례식에 수치값을 대입하면 다음과 같습니다.

1 : count/n = 1 : π/4

몬테카를로 방법을 통해 실제와 가까운 해를 얻기 위해서는 방대한 단순 계산을 매우 빠르게 처리할 수 있는 컴퓨터가 필수입니다. 이 몬테카를로 방법은 핵폭탄이나 수소폭탄의 개발에서 핵심적인 역활을 담당했다고 합니다. 제 경우도 핵폭탄 개발이 필요해서... 가 아닌 강화학습(Reinforcement learning)의 한 방법으로 접하게 되었습니다.

답글 남기기 응답 취소