패턴명칭
Mediator
필요한 상황
객체들 간의 상태가 또 다른 객체의 상태 변화에 영향을 줄때 각 객체의 상태 변화를 개별 객체가 읽어 처리하기 보다 하나의 중개자(Mediator)를 두어 처리할 수 있다.
예제 코드
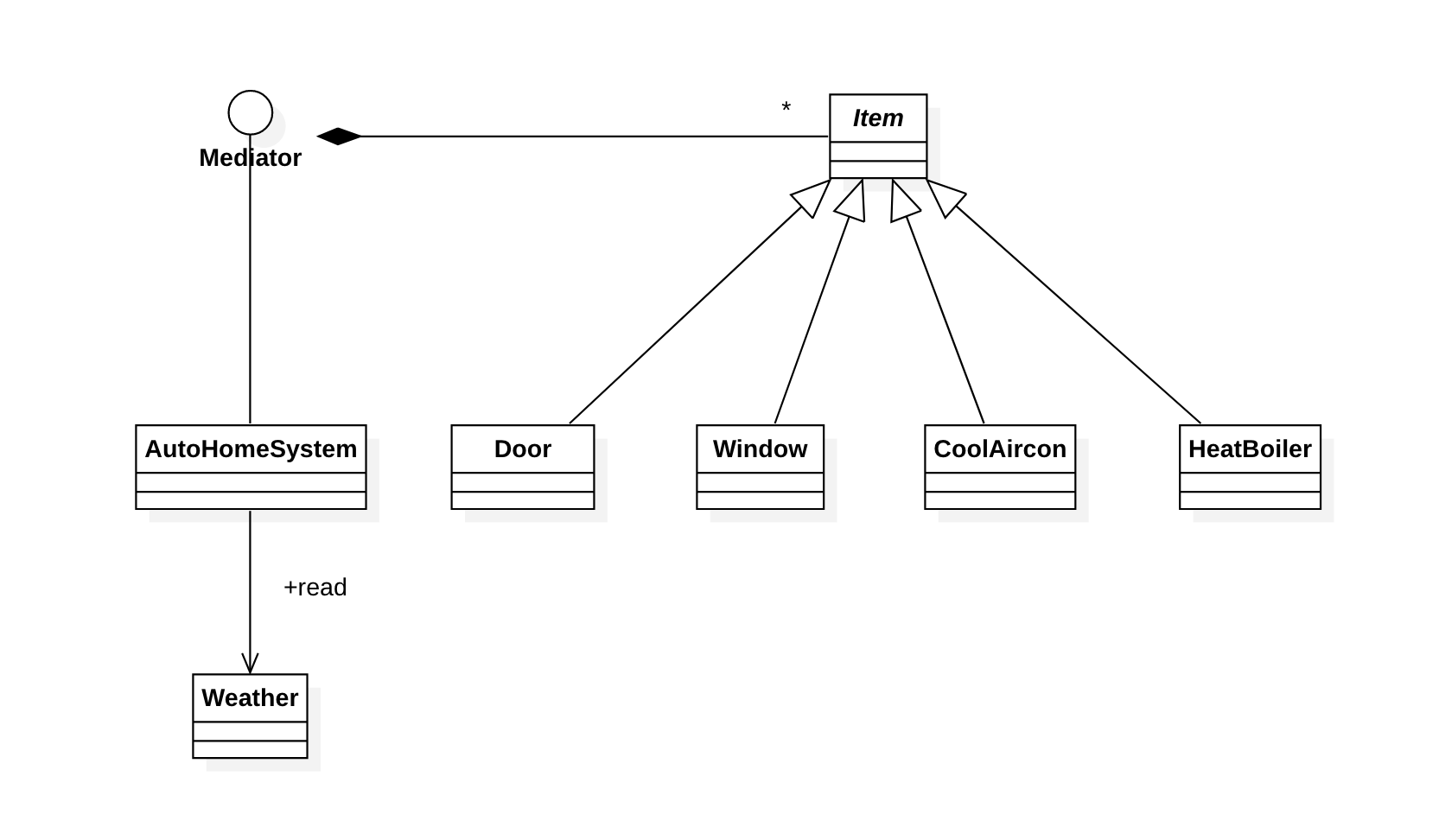
날씨 정보에 따라 집안의 문, 창, 에어컨, 보일러의 가동을 자동화하는 예제이다. 비가 오면 창을 닫고 온도가 0도 보다 떨어지면 보일러를 켜고 에이컨을 끈다. 그리고 온도가 30가 넘어가면 에어컨을 켜고 보일러를 끈다. 또한 문, 창, 에이컨, 보일러의 상태가 변경되면 중개자에게 상태 변경을 알리고 중개자는 상태에 따라 각 객체를 제어하는데, 에이컨을 가동 상태로 변경하면 보일러를 끄고 문과 창을 닫는다. 그리고 보일러를 가동 상태로 변경하면 에이컨을 끄고 문과 창을 닫는다. 문이나 창이 열리는 상태로 변경되면 보일러와 에어컨을 끈다.
중개자는 Mediator 인터페이스로 구현해야 하며 다음과 같다.
package tstThread;
public interface Mediator {
void itemsChanged();
}
Item은 앞서 언급한 문, 창, 에이컨, 보일러에 대한 구체적인 클래스가 반드시 구현해야할 추상 클래스로 다음과 같다.
package tstThread;
public abstract class Item {
protected Mediator mediator;
public Item(Mediator mediator) {
this.mediator = mediator;
}
}
중개자를 구현한 AutoHomeSystem 클래스는 다음과 같다.
package tstThread;
public class AutoHomeSystem implements Mediator {
private Door door = new Door(this);
private Window window = new Window(this);
private CoolAircon aircon = new CoolAircon(this);
private HeatBoiler boiler = new HeatBoiler(this);
public void checkWeather(Weather weather) {
if(weather.isRain()) {
window.close();
}
int temperature = weather.getTemperature();
if(temperature < 10) {
aircon.off();
boiler.on();
} else if(temperature > 30) {
aircon.on();
boiler.off();
} else {
aircon.off();
boiler.off();
}
}
public void itemsChanged() {
if(aircon.isRunning()) {
boiler.off();
window.close();
door.close();
}
if(boiler.isRunning()) {
aircon.off();
window.close();
door.close();
}
if(!door.isClosed() || !window.isClosed()) {
aircon.off();
boiler.off();
}
}
public void report() {
System.out.println("\t" + door);
System.out.println("\t" + window);
System.out.println("\t" + aircon);
System.out.println("\t" + boiler);
}
}
위의 코드를 보면 중개자가 날씨와 문, 창, 에어컨, 보일러의 상태를 검사하여 다른 객체의 상태를 제어하고 있다. 날씨 클래스를 보자.
package tstThread;
import java.util.Random;
public class Weather {
private boolean bRain = false;
private int temperature = 0;
private Random random = new Random();
public void update() {
bRain = random.nextInt(4) >= 3;
temperature = (int)(random.nextDouble() * 100.0 - 50.0);
}
public boolean isRain() {
return bRain;
}
public int getTemperature() {
return temperature;
}
public String toString() {
return "[ Rain: " + bRain + ", Temperature: " + temperature + " ]";
}
}
이제 Item 추상 클래스를 구현하는 클래스들을 살펴보자. 먼저 Door 이다.
package tstThread;
public class Door extends Item {
private boolean bClosed = false;
public Door(Mediator mediator) {
super(mediator);
}
public void open() {
if(!bClosed) return;
bClosed = false;
mediator.itemsChanged();
}
public void close() {
if(bClosed) return;
bClosed = true;
mediator.itemsChanged();
}
public boolean isClosed() {
return bClosed;
}
public String toString() {
StringBuilder sb = new StringBuilder();
sb.append("DOOR: ");
if(bClosed) {
sb.append("closed");
} else {
sb.append("opened");
}
return sb.toString();
}
}
다음은 Window 클래스이다.
package tstThread;
public class Window extends Item {
private boolean bClosed = false;
public Window(Mediator mediator) {
super(mediator);
}
public void open() {
if(!bClosed) return;
bClosed = false;
mediator.itemsChanged();
}
public void close() {
if(bClosed) return;
bClosed = true;
mediator.itemsChanged();
}
public boolean isClosed() {
return bClosed;
}
public String toString() {
StringBuilder sb = new StringBuilder();
sb.append("Window: ");
if(bClosed) {
sb.append("closed");
} else {
sb.append("opened");
}
return sb.toString();
}
}
다음은 CoolAircor 클래스이다.
package tstThread;
public class CoolAircon extends Item {
private boolean bOff = true;
public CoolAircon(Mediator mediator) {
super(mediator);
}
public void on() {
if(!bOff) return;
bOff = false;
mediator.itemsChanged();
}
public void off() {
if(bOff) return;
bOff = true;
mediator.itemsChanged();
}
public boolean isRunning() {
return !bOff;
}
public String toString() {
StringBuilder sb = new StringBuilder();
sb.append("CoolAircon: ");
if(bOff) {
sb.append("off");
} else {
sb.append("on");
}
return sb.toString();
}
}
다음은 HeatBoiler 클래스이다.
package tstThread;
public class HeatBoiler extends Item {
private boolean bOff = true;
public HeatBoiler(Mediator mediator) {
super(mediator);
}
public void on() {
if(!bOff) return;
bOff = false;
mediator.itemsChanged();
}
public void off() {
if(bOff) return;
bOff = true;
mediator.itemsChanged();
}
public boolean isRunning() {
return !bOff;
}
public String toString() {
StringBuilder sb = new StringBuilder();
sb.append("HeatBoiler: ");
if(bOff) {
sb.append("off");
} else {
sb.append("on");
}
return sb.toString();
}
}
지금까지의 클래스를 사용하는 예제는 다음과 같다.
package tstThread;
public class Main {
public static void main(String[] args) throws InterruptedException {
Weather weather = new Weather();
AutoHomeSystem home = new AutoHomeSystem();
do {
weather.update();
System.out.println("Today's weather -> " + weather);
home.checkWeather(weather);
home.report();
Thread.sleep(2000);
System.out.println();
} while(true);
}
}
실행 결과는 다음과 같다.
Today's weather -> [ Rain: false, Temperature: -22 ] DOOR: closed Window: closed CoolAircon: off HeatBoiler: on Today's weather -> [ Rain: false, Temperature: 40 ] DOOR: closed Window: closed CoolAircon: on HeatBoiler: off Today's weather -> [ Rain: false, Temperature: -40 ] DOOR: closed Window: closed CoolAircon: off HeatBoiler: on Today's weather -> [ Rain: false, Temperature: 41 ] DOOR: closed Window: closed CoolAircon: on HeatBoiler: off Today's weather -> [ Rain: false, Temperature: 45 ] DOOR: closed Window: closed CoolAircon: on HeatBoiler: off