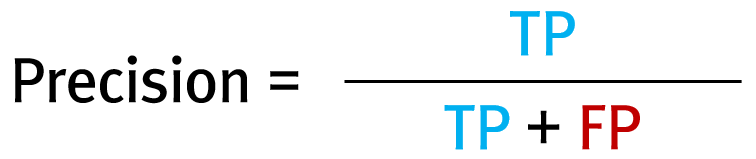사진 이미지는 촬영된 주변 환경에 따라 그 명도나 채도 등이 서로 다릅니다. 이 사진 이미지를 대상으로 하는 머신러닝을 수행하기 전에 이미지들을 동일한 환경으로 맞춰주는 후처리로 전체 이미지에 대한 화소값의 평균과 표준편차를 구해 이 값을 이미지들에 일괄적으로 적용합니다.
아래의 코드는 PyTorch에서 Dataset에 대한 평균과 표준편차를 구하기 위한 코드입니다.
transform = transforms.Compose([
transforms.ToTensor()
])
dataset = torchvision.datasets.CIFAR10(root='./data/cifar10', train=True, download=True, transform=transform)
mean = dataset.train_data.mean(axis=(0,1,2))
std = dataset.train_data.std(axis=(0,1,2))
mean = mean / 255
std = std / 255
실제 mean과 std의 값은 각각 [0.4913, 0.4821, 0.4465], [0.2470, 0.2434, 0.2615]와 유사한데, 실제 CIFAR10 데이터를 이용한 딥러닝 예제 코드에서 상수값으로 입력되는 바로 그 값입니다. 실제로 이 평균과 편차는 다음 코드 예시를 통해 적용됩니다.
train_transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize(mean, std)
])
train_dataset = torchvision.datasets.CIFAR10(root='./data/cifar10', train=True, download=True, transform=train_transform)