신경망을 이용한 비선형 모델의 회귀분석

딥러닝을 위한 신경망은 기본적으로 선형회귀분석을 기반으로 합니다. 선형 회귀 분석이라는 전제 조건은 아주 복잡한 모델, 즉 비선형인 형태의 모델은 추론할 수 없지만, 신경망의 층(Layer)를 깊게 쌓으면서 그 중간에 비선형성을 부여하는 활성화 함수를 넣어주게 되면 선형회귀분석에 기반한 신경망으로도 아주 복잡한 비선형 모델도 추론할 수 있다는 것입니다. 예를 들어, 아래와 같은 분포를 가지는 데이터셋에 대한 회귀분석도 가능합니다.

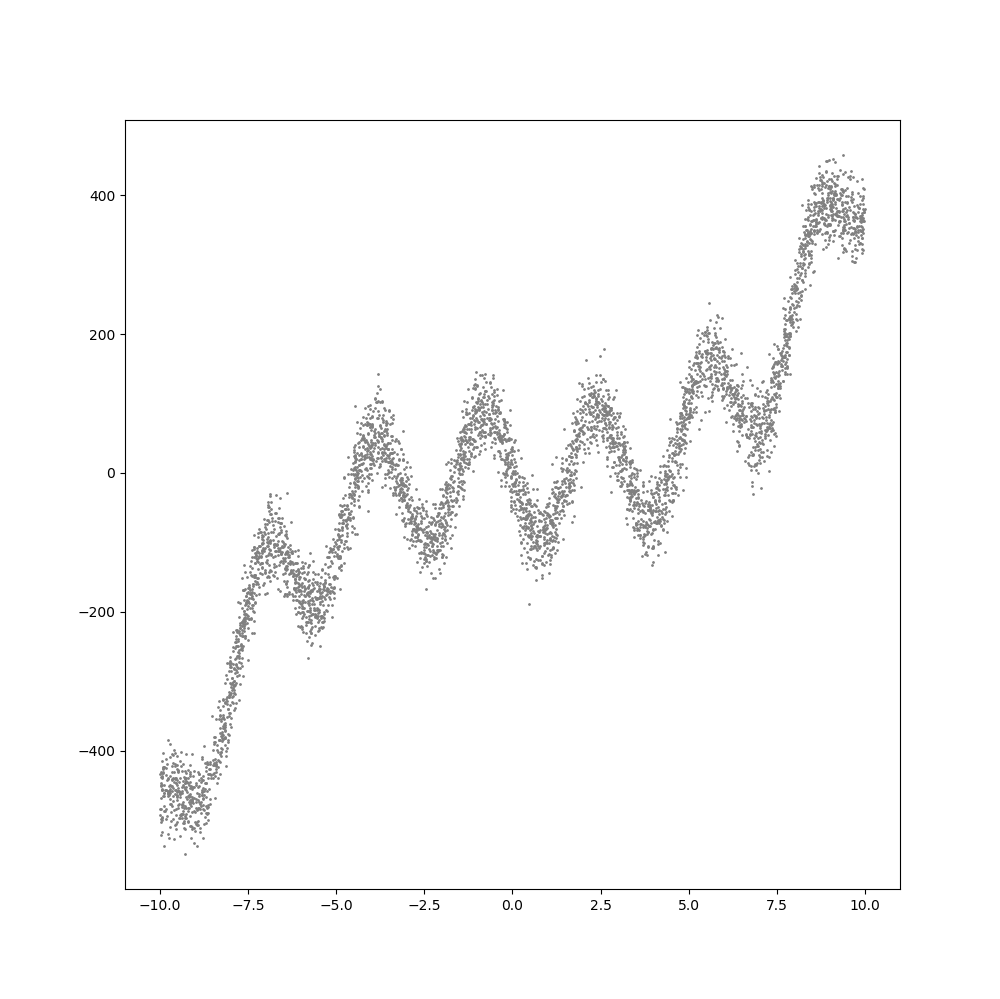
위의 데이터는 다음과 같은 공식에 대해서, y값에 표준편차 30인 정규분포의 잡음(Noise)를 추가해 생성한 것입니다.

$y = 0.5 \times x^{3} - 0.5 \times x^{2} - 90 \times sin(x^{2}) + 1$

이제 위의 데이터셋을 이용해 딥러닝 학습을 통해 비선형 모델에 대한 추론에 대한 코드를 정리하겠습니다. 코드는 파이선으로, 그리고 딥러닝 라이브러리는 파이토치를 사용했습니다.

먼저 필요한 패키지를 임포트합니다.

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.init as init
import matplotlib.pyplot as plt

학습을 위해 데이터가 필요한데, 앞서 언급한 공식을 활용하여 총 5000개의 (x, y) 값의 데이터를 생성합니다. 물론 y 값에는 마찬가지로 앞서 언급한 표준편차가 30인 정규분포로 생성된 잡음을 반영합니다. 아래는 이에 대한 코드입니다.

num_data = 5000
noise = init.normal_(torch.FloatTensor(num_data,1), std=30)
x = init.uniform_(torch.Tensor(num_data,1),-10,10)

def func(x): return 0.5*(x**3) - 0.5*(x**2) - torch.sin(2*x)*90 + 1 
y_noise = func(x) + noise

신경망 모델을 생성합니다. 신경망 모델에 대한 코드는 아래와 같습니다.

model = nn.Sequential(
    nn.Linear(1,5),
    nn.LeakyReLU(0.2),
    nn.Linear(5,10),
    nn.LeakyReLU(0.2),
    nn.Linear(10,10),
    nn.LeakyReLU(0.2),    
    nn.Linear(10,10),
    nn.LeakyReLU(0.2),        
    nn.Linear(10,5),
    nn.LeakyReLU(0.2),          
    nn.Linear(5,1),
)

위의 신경망을 도식화하면 다음과 같습니다.

활성화 함수로 Leaky ReLU를 사용한 이유는, Sigmoid의 경우 기울기 소실이 발생하여 학습이 잘이루어지지 않고 일반 ReLU를 사용할 경우 학습 대상이 되는 가중치와 편향이 음수가 될 경우에 입력값까지 음수가 되면 최종 활성화 값이 항상 0이 되어 이 값이 뉴런에 전달되고, 전달 받은 뉴런이 제 역활을 하지 못하는 현상(문헌에서는 Dying Neuron이라고 함)이 발생하기 때문입니다 Leaky ReLU는 기울기 소실 문제와 입력값이 음수일때에도 일반 ReLU처럼 0이 아닌 가중치(위에서는 0.2)가 반영된 값이 활성값으로 결정되어 Dying Neuron 현상을 막아줍니다.

다음은 학습에 대한 코드입니다.

gpu = torch.device('cuda')
loss_func = nn.L1Loss().to(gpu)
optimizer = torch.optim.Adam(model.parameters(), lr=0.002)

model = model.to(gpu)
x = x.to(gpu)
y_noise = y_noise.to(gpu)

num_epoch = 20000
loss_array = []
for epoch in range(num_epoch):
    optimizer.zero_grad()
    output = model(x)
    
    loss = loss_func(output,y_noise)
    loss.backward()
    optimizer.step()
    
    loss_array.append(loss)

    if epoch % 100 == 0:
        print('epoch:', epoch, ' loss:', loss.item())

손실값은 매우 단순한 L1 손실을 사용는데, 위의 학습을 위한 데이터셋의 경우 오차값의 절대값이 L1 값이고 오차값에 대해 손실값이 비례하므로 L1 손실은 적당하고 학습 속도가 빠릅니다. 그리고 가중치에 대한 최적화 방법은 Adam을 사용했습니다. 일반 SGD 방식은 그 방식이 매우 단순해서 좀처럼 학습이 되지 않습니다.

이제 학습 동안 손실값의 추이와 추론된 신경망의 모델에 대한 결과를 그래프로 나타내기 위한 코드는 다음과 같습니다.

plt.plot(loss_array)
plt.show()

plt.figure(figsize=(10,10))

x = x.cpu().detach().numpy()
y_noise = y_noise.cpu().detach().numpy()
output = output.cpu().detach().numpy()

plt.scatter(x, y_noise, s=1, c="gray")
plt.scatter(x, output, s=1, c="red")

plt.show()

위 코드에서 손실에 대한 그래프 결과는 다음과 같습니다.

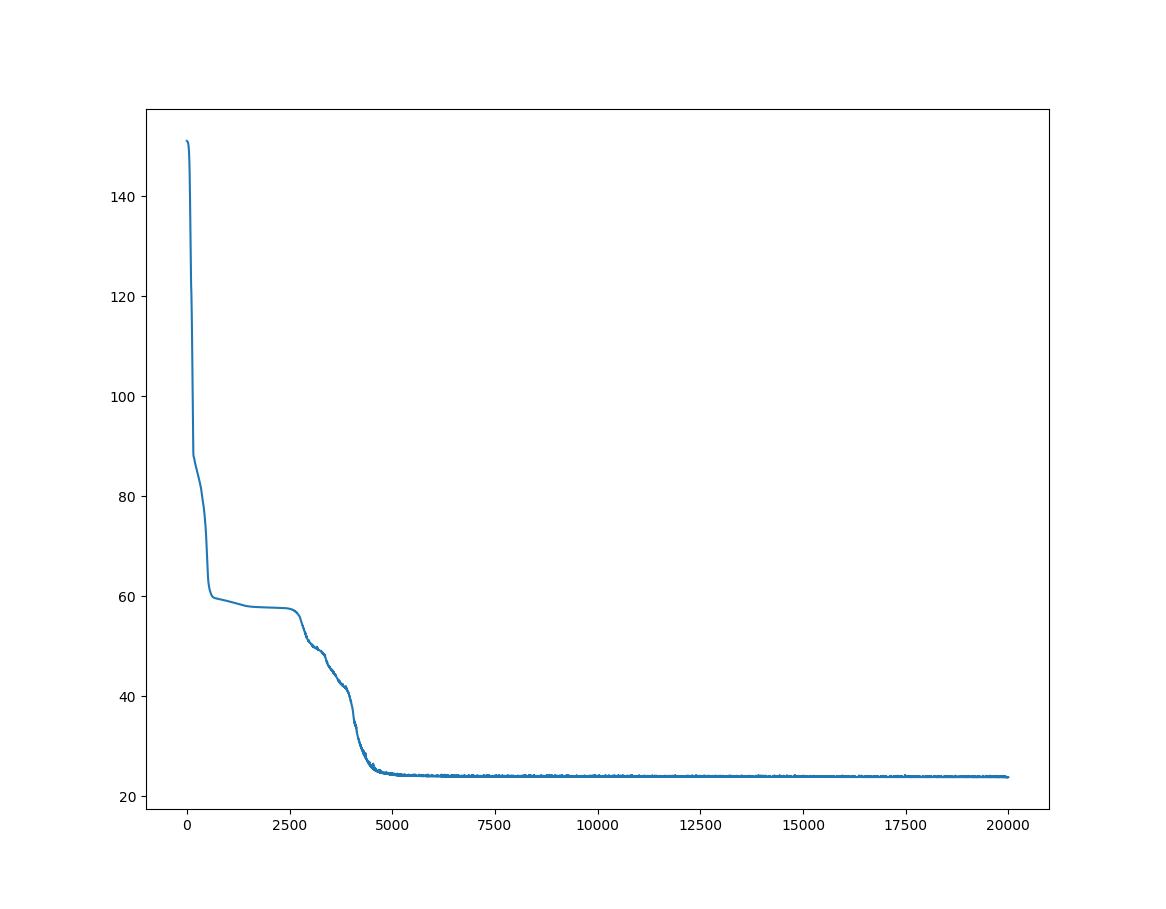
손실값이 매 에폭마다 감소하는 것을 보면 학습이 제대로 이루어지고 있다는 것을 알 수 있습니다. 그리고 가장 중요한 그래프인, 신경망 학습의 추론 결과에 대한 그래프입니다.

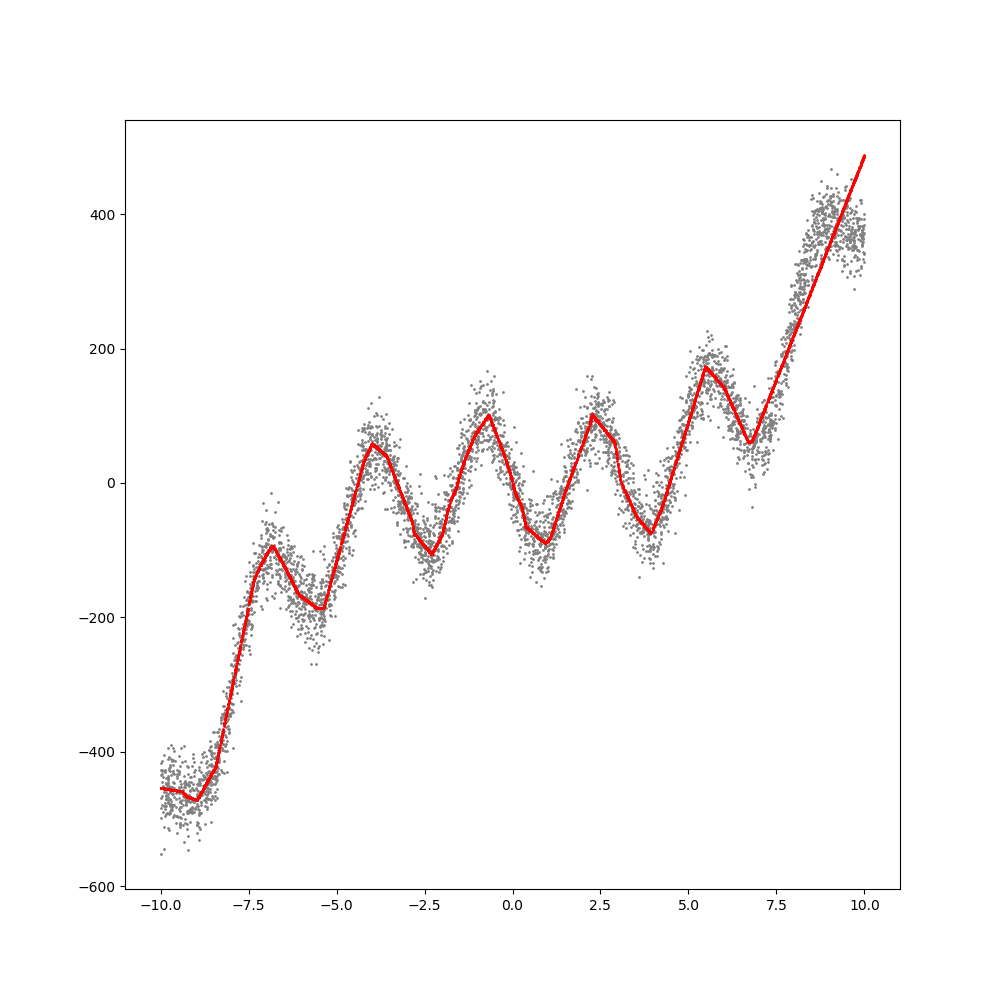
회색 지표는 학습 데이터이고 빨간색 지표가 학습된 모델이 추론한 결과입니다. 데이테에 매우 근접한 추론 결과를 나타내고 있는 것을 볼 수 있습니다. 그래프가 곡선처럼 보이지만 사실은 직선으로 구성된 그래프입니다. 이는 앞서 언급했듯이 신경망이 선형회귀에 기반하고 있기 때문입니다.

답글 남기기 응답 취소