이 글의 원문은 https://opencv-python-tutroals.readthedocs.io/en/latest/py_tutorials/py_ml/py_svm/py_svm_basics/py_svm_basics.html 입니다.
선형으로 분리될 수 있는 데이터
빨간색과 파란색에 대한 두 종류의 데이터에 대한 아래의 그림을 봅시다. kNN에서는, 테스트 데이터에 대해서, 훈련을 위한 전체 데이터와의 거리를 측정하여 최소 거리를 가지는 것 하나를 구했습니다. 이는 훈련 데이터 전체를 저장하고 모든 거리를 구해야 하므로 메모리를 많이 활용하고, 계산 시간도 많이 소요됩니다. 그러나 아래의 이미지처럼 주어진 데이터에 대해도 이처럼 많은 자원이 필요할까요?
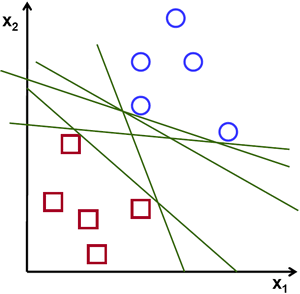
생각을 바꿔서, 두 영역으로 데이터를 분리하는 어떤 선, 
가 있습니다. 새로운 시험 데이터 
가 있다면, 이를 
에 대입해서, 
이면 파란색 그룹에 속하고, 그렇지 않다면 빨간색 그룹에 속한다고 할 수 있습니다. 이러한 선을 결정 경계(Decsion Boundary)라고 부를 수 있습니다. 이는 매우 단순하며 메모리 효율성이 높습니다. 직선(또는 더 높은 차원에서는 평면)으로 두 영역으로 나눌 수 있는 이러한 데이터를 선형으로 나눠질 수 있다라고 합니다.
위의 이미지에서, 이러한 선은 매우 많습니다. 이 중 어떤 선을 선택해야 할까요? 매우 직관적으로, 모든 데이터로부터 가능한 멀리 떨어져 통과하는 선이라고 할 수 있습니다. 왜냐면, 입력 데이터에 잡음이 있을 수 있기 때문입니다. 이런 선은 분류 정확도에 영향을 줘서는 안됩니다. 가정 멀리 떨어진 선을 사용하는 것은 잡음에 대해 더 강하다는 의미입니다. 그래서 SVM(Support Vector Machines)이란 이러한 작선(또는 평면)을 얻는 것입니다. 아래의 그림에서 굷은 선이 바로 그 것입니다.
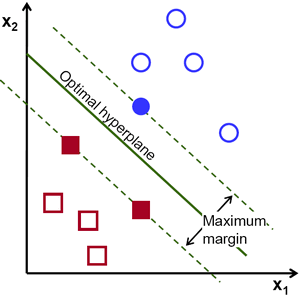
결정 경계(Decision Boundary)을 찾기 위해서는 훈련 데이터(Training Data)가 필요합니다. 그렇다면 전체 훈련 데이터가 필요할까요? 단지 상대 그룹과 가까운 것들만으로도 충분합니다. 위의 그림에서는 하나의 파란색 원과 두개의 빨간색 사각형이면 충분합니다. 바로 이 데이터를 지지 벡터(Support Vectors)라고 하며, 이 데이터를 통과하는 선들을 지지 평면(Support Planes)이라고 합니다. 이 것은 결정 경계를 구하는데 충분한 기반이 됩니다.
가장 멋진 지지 평면을 찾기 위한 수학적인 모델을 생각해 봅시다. 예를 들어서, 파란색 데이터는 
로 나타낼 수 있는 반면, 빨간색 데이터는 
로 나타낼 수 있습니다. 
는 가중치 벡터(Weight Vector)(
)이며, 
는 픽쳐 벡터(Feature Vector)(
)입니다. 
는 편향(Bias)입니다. 가중치 벡터는 분리 경계의 방향을 결정하며, 편향은 위치를 결정합니다. 결정 경계는 이러한 평면 사이의 중앙을 지나는 것으로 정의될 수 있고, 
로 표현할 수 있습니다. 지지 벡터에서 결정 경계 사이의 최소한의 거리는 
로 주어집니다. 이 거리의 2배가 위 그림에서의 빈공간(Margin)이며, 이 빈공간이 최대화되어야 합니다. 예를들어, 아래와 같은 제약조건을 가지는 새로운 함수 
를 최소화할 필요가 있습니다.
위의 식에서 
는 
인 각 군(class)의 라벨입니다.
비선형으로 분리할 수 있는 데이터
직선으로 분리할 수 없는 어떤 데이터를 생각해 봅시다. 예를 들어서, ‘X’가 -3과 +3이고 ‘O’가 -1과 +1인 1차원 데이터 말입니다. 이 데이터는 선형으로 분리될 수 없음이 명백합니다. 그렇지만 이러한 문제를 해결할 수 있는 방법이 존재합니다. 이 데이터를 
함수를 통해 ‘X’는 9가 되고, ‘O’는 1이 되어 선형으로 분리되어 집니다.
반면에 1차원 데이터를 2차원 데이터로 변환할 수 있습니다. 
함수를 이용해 ‘X’는 (-3,9)와 (3,9)가 되고 ‘O’는 (-1,1)과 (1,1)이 되며, 이는 선형으로 분리됩니다. 요약하면, 낮은 차원 공간에서의 비선형으로 분리되어지는 데이터는 더 높은 차원 공간에서는 선형으로 분리될 수 있는 더 많은 가능성이 있습니다.
일반적으로 D>d일때, d차원 공간에서의 포인트들이 D-차원 공간으로 맵핑될때 선형으로 분리될 가능성이 높아집니다. 여기에 낮은 차원으로 입력된 (피쳐;feature) 공간에서의 계산으로 높은 차원 (커널;kernel) 공간에서 내적(dot product)를 계산하는데 도움이 되는 방법이 존재합니다. 다음의 예로 설명해 보겠습니다.
2차원 공간에서 2개의 포인트(
, 
)를 생각해 봅시다. 
를 2차원에서 3차원 공간으로 맵핑하는 함수라고 할때 아래와 같습니다.
커널 함수 
를 아래와 같이 정의하면, 이 함수는 두 포인트 사이의 내적(dot product)입니다.
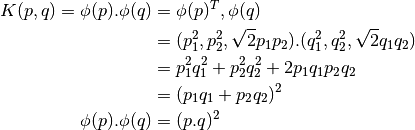
이는, 3차원 공간에서의 내적은 2차원 공간에서의 내적의 제곱이라는 의미입니다. 이를 더 높은 차원의 공간에서 적용할 수 있습니다. 그래서 더 낮은 차원에서의 데이터를 그대로 더 높은 차원으로 계산할 수 있습니다. 일단 이렇게 맵핑되면, 더 높은 차원의 공간에서의 데이터를 얻을 수 있습니다.
지금까지의 모든 개념에 덧붙여, 여기에는 잘못된 분류에 대한 문제가 존재합니다. 그래서 단순히 최대 빈공간(Margin)을 갖는 결정 경계(Decision Boundary)를 찾는 것만으로는 충분하지 않습니다. 잘못된 분류에 대한 문제도 함께 고려해야 합니다. 때때로, 더 나은 분류를 제공하는 더 작은 빈공간을 갖는 결정공간이 존재할 수 있습니다. 어째거나, 최대한의 빈공간을 가지면서 더 적은 분류 오류를 제공하는 결정 경계를 찾아야만합니다. 최소화된 기준은 다음과 같습니다.
아래 그림이 이러한 개념을 나타냅니다. 훈련 데이터의 각 샘플에 대해서, 새로운 파라메터 
가 정의됩니다. 이 파라메터는 훈련 데이터와 수정된 결정 영역 사이의 거리입니다. 여기에는 잘못된 분류가 없는데, 지지 평면에 샘플 데이터가 옳바르게 떨어지고, 거리는 0입니다.
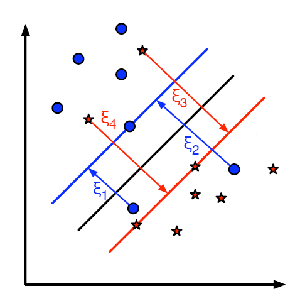
이제 새로운 최적화된 문제는 다음과 같습니다.
위의 식에서 인자 C는 어떻게 정해야 할까요? 이에 대한 대답은 시험 데이터가 어떻게 분포되었느냐에 따라 결정된다입니다. 비록 일반화된 방법은 없지만 다음과 같은 규칙을 따르면 좋습니다.
- 큰 C 값은 분류에 대한 작은 오차를 제공하지만 빈공간(Margin)이 더 작아지게 된다. 최적화의 목표가 인자의 최소화에 있으므로, 약간의 분류 오차가 허용된다.
- 작은 C 값은 더 큰 빈공간을 제공하지만 분류 시 더 많은 오차가 존재한다. 큰 빈공간을 가지는 평면을 찾는 것에 더 중요한 목표이므로 최소화는 고려되지 않는 경우이다.