이 글의 원문은 https://opencv-python-tutroals.readthedocs.io/en/latest/py_tutorials/py_calib3d/py_epipolar_geometry/py_epipolar_geometry.html 입니다.Epipolar Geometry는 영어이고, 등극선 기하는 중국 한자이고.. ㅜ_ㅜ 잠시 생각이 많아집니다. 그냥 이 용어에 대해서는 어떠한 어설픈 번역없이 Epipolar Geometry라고 하겠습니다. 네, 이 글은 Epipolar Geometry에 대한 글입니다. Epipolar Geometry가 무엇인지부터 파악하고 Epipolar Geometry와 연관된 Epiline, Epipole를 구하는 OpenCV의 함수를 살펴보겠습니다. 물론 이러한 설명 중에 왜! Epipolar Geometry가 필요한지도 파악할 것입니다.
카메라를 통해 이미지를 촬영할 때, 이미지의 깊이라는 중요한 정보가 소실됩니다. 달리 말해 3차원에서 2차원으로 변환되므로 카메라의 위치에서 이미지의 각 지점이 얼마나 멀리 떨어져 있는지 알 수 없습니다. 그래서 그래서 이러한 카메라를 이용하여 깊이 정보를 얻을 수 있는지에 대한 것은 중요한 문제입니다. 그리고 그에 대한 대답은 하나 이상의 카메라를 이용한다면 가능하다입니다. 우리의 두 눈은 2개의 카메라에 비유할 수 있는데, 이처럼 2대의 카메라를 이용한 Vison 영역을 스테레오 비전(Stero Vision)이라고 합니다. 스테레오 비전을 위해 OpenCV에서 제공하는 것은 무엇인지도 살펴 보겠습니다. (이러한 분야를 위해 Learing OpenCV by Gray Bradsky 가 많은 정보를 제공합니다.)
깊이 정보 이미지를 살펴보기 전에, 먼저 다중뷰 지오메트리에 대한 기본 개념을 살펴봅시다. 아래의 이미지는 2대의 카메라를 설치하고 동일한 장면에 대한 이미지를 촬영하는 것에 대한 개념도입니다.
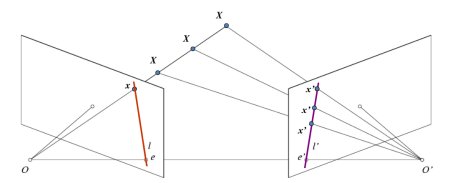
왼쪽 카메라만을 사용한다면, 이미지의 x 지점에 해당하는 3차원 포인트를 알 수 없는데, 이는 선 OX 상의 모든 지점이 이미지 평면 상에 동일한 지점에 투영되기 때문입니다. 그러나 오른쪽 이미지도 한번 살펴 봅시다. 선 OX 상에 서로 다른 지점들은 오른쪽 이미지 평면에서는 서로 다른 지점(x’)으로 투영됩니다. 그래서 이러한 2개의 이미지를 이용해, 정확한 3차원 지점을 3각 측량이 가능하게 됩니다.
왼쪽의 선 OX 상에 다른 지점의 투영은 오른쪽 이미지 평면에 하나의 선(l’)을 구성합니다. 이 선을 x 지점에 해당하는 epiline라고 합니다. 이는 오른쪽 이미지 위에 x 지점을 찾기 위해 이 epiline을 따라 찾으면 된다는 의미입니다. 이 선 상 어디엔가 존재해야만 합니다. (이 방법을 생각해 보면, 다른 이미지에서 매칭되는 지점을 찾기 위해, 전체 이미지를 조사할 필요가 없고, 단지 epiline 상의 지점만을 조사하면 된다는 것입니다.) 이를 Epipolar Constraint라고 합니다. 유사하게 모든 지점은 다른 이미지 상에 각각에 해당하는 epline을 가지고 있습니다. 평면 XOO’를 Epipolar Plane라고 합니다.
O와 O’는 카메라의 중심입니다. 위의 그림의 설정에서, 오른쪽 카메라 O’는 왼쪽 이미지에서 지점 e에 투영됩니다. 이 지점 e를 Epipole이라고 합니다. Epipole는 이미지 평면과 카메라 중심을 관통하는 교차점입니다. 동일하게 e’는 왼쪽 카메라의 Epipole 입니다. 이미지에서 Epipole를 발견할 수 없는 경우가 있는데, 이는 Epipole이 이미지 밖에 존재할 수 있기 때문입니다(이는 하나의 카메라가 다른 케마라는 보고 있지 않다는 의미임).
모든 Epiline는 Epipole을 지납니다. 그래서 Epipole을 찾기 위해서 많은 Epiline를 찾을 수 있고, 이 Epiline과의 교차점을 찾을 수 있습니다.
결국 이 글에서는, Epipolar 선과 Epipole를 구하는 것이 핵심입니다. 이를 구하기 위해서 2개의 구성요소가 필요한데, Fundamental Matrix와 Essential Matrix이며 각각을 F와 E라고 하겠습니다. E는 전역 좌표계(Global Coordinate) 상의 첫번째 카메라와 연관된 두번째 카메라의 위치를 나타내는 이동과 회전에 대한 정보를 가지고 있습니다. 아래의 이미지(출처 : Learning OpenCV by Gary Bradsky)를 참고합시다.
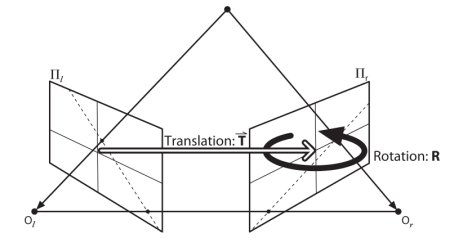
그러나 우리는 픽셀 좌표계로 측정하는 것을 선호합니다. F는 E와 동일한 정보를 포함하고 있으면서 두 카메라의 고유한 정보를 추가적으로 가지고 있어서 픽셀 좌표로 두 카메라를 연관 지을 수 있습니다. (만약 보정된 이미지를 사용하고 초점 거리에 의해 나눠진 지점을 정규하시키면 F와 E는 동일합니다.) 간단히 말해, F는 하나의 이미지 상의 한 지점을 다른 이미지 상의 하나의 선(Epiline)에 맵핑됩니다. 이는 두 이미지로부터 매치되는 지점으로부터 계산됩니다. F를 구하기 위해서 최소한 8개의 이러한 지점이 필요(8-point 알고리즘)합니다. 더 많은 지점이 있다면 좋으며 RANSAC를 사용하면 더 좋은 결과를 얻을 수 있습니다.
이제 OpenCV를 이용한 예제 코드를 살펴보겠습니다. 가장 먼저 2개의 이미지(동일한 피사체를 왼쪽과 오른쪽에서 촬용한) 사이에 매칭되는 특징점을 최대한 많이 찾아내야 합니다. 이를 위해 FLANN에 기반한 매처를 이용한 SIFT 디스크립터를 사용하고 ratio 테스트합니다.
import cv2
import numpy as np
from matplotlib import pyplot as plt
img1 = cv2.imread('./data/dvd_left.jpg',0) #queryimage # left image
img2 = cv2.imread('./data/dvd_right.jpg',0) #trainimage # right image
sift = cv2.xfeatures2d.SIFT_create()
# find the keypoints and descriptors with SIFT
kp1, des1 = sift.detectAndCompute(img1,None)
kp2, des2 = sift.detectAndCompute(img2,None)
# FLANN parameters
FLANN_INDEX_KDTREE = 0
index_params = dict(algorithm = FLANN_INDEX_KDTREE, trees = 5)
search_params = dict(checks=50)
flann = cv2.FlannBasedMatcher(index_params,search_params)
matches = flann.knnMatch(des1,des2,k=2)
good = []
pts1 = []
pts2 = []
# ratio test as per Lowe's paper
for i,(m,n) in enumerate(matches):
if m.distance < 0.8*n.distance:
good.append(m)
pts2.append(kp2[m.trainIdx].pt)
pts1.append(kp1[m.queryIdx].pt)
두 이미지로부터 매칭되는 특징점 중 가장 좋은 것들을 이용해 Fundamental Matrix를 계산합니다.
pts1 = np.int32(pts1) pts2 = np.int32(pts2) F, mask = cv2.findFundamentalMat(pts1,pts2,cv2.FM_LMEDS) # We select only inlier points pts1 = pts1[mask.ravel()==1] pts2 = pts2[mask.ravel()==1]
다음은 Epiline를 찾아야 합니다. 첫번째 이미지의 지점에 해당하는 Epiline은 두번재 이미지에 그려집니다. 선에 대한 배열이 얻어집니다. 이러한 선을 이미 상에 그리는 함수를 정의했는데, 아래와 같습니다.
def drawlines(img1,img2,lines,pts1,pts2):
''' img1 - image on which we draw the epilines for the points in img2
lines - corresponding epilines '''
r,c = img1.shape
img1 = cv2.cvtColor(img1,cv2.COLOR_GRAY2BGR)
img2 = cv2.cvtColor(img2,cv2.COLOR_GRAY2BGR)
for r,pt1,pt2 in zip(lines,pts1,pts2):
color = tuple(np.random.randint(0,255,3).tolist())
x0,y0 = map(int, [0, -r[2]/r[1] ])
x1,y1 = map(int, [c, -(r[2]+r[0]*c)/r[1] ])
img1 = cv2.line(img1, (x0,y0), (x1,y1), color,1)
img1 = cv2.circle(img1,tuple(pt1),5,color,-1)
img2 = cv2.circle(img2,tuple(pt2),5,color,-1)
return img1,img2
이제, 두 이미지에서 Epiline를 찾아 그려줍니다.
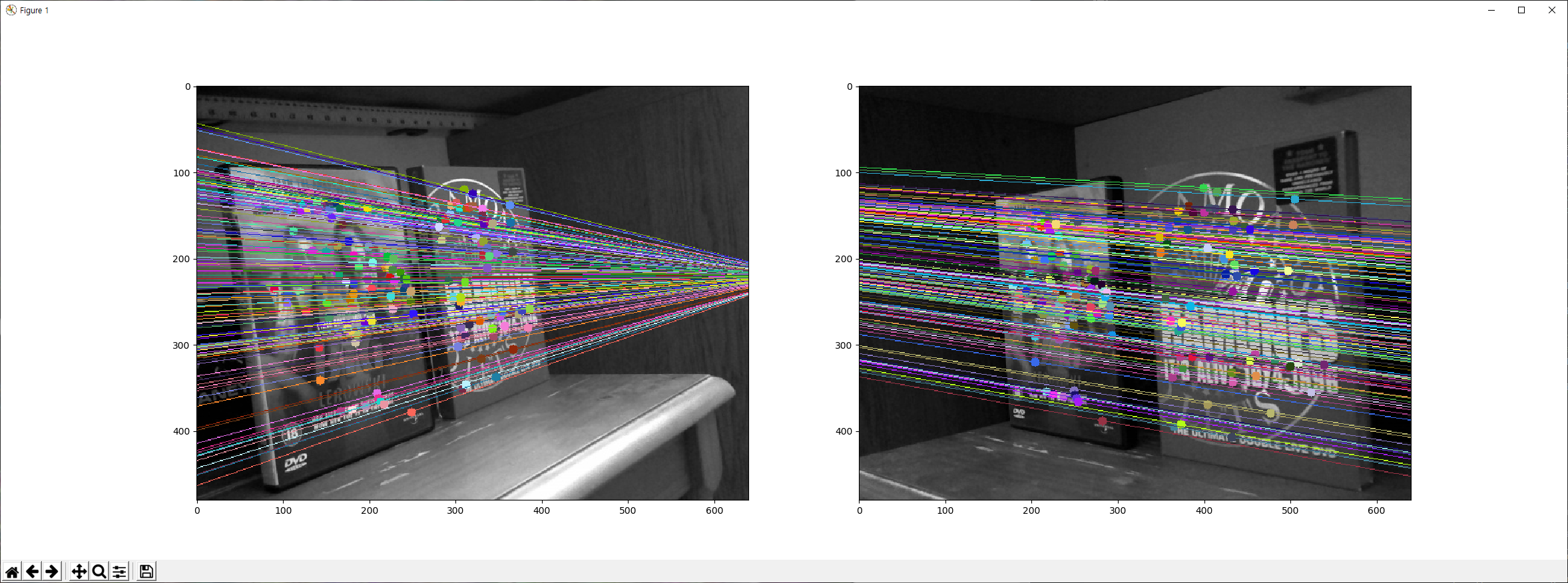
# Find epilines corresponding to points in right image (second image) and # drawing its lines on left image lines1 = cv2.computeCorrespondEpilines(pts2.reshape(-1,1,2), 2,F) lines1 = lines1.reshape(-1,3) img5,img6 = drawlines(img1,img2,lines1,pts1,pts2) # Find epilines corresponding to points in left image (first image) and # drawing its lines on right image lines2 = cv2.computeCorrespondEpilines(pts1.reshape(-1,1,2), 1,F) lines2 = lines2.reshape(-1,3) img3,img4 = drawlines(img2,img1,lines2,pts2,pts1) plt.subplot(121),plt.imshow(img5) plt.subplot(122),plt.imshow(img3) plt.show()
결과는 다음과 같습니다.