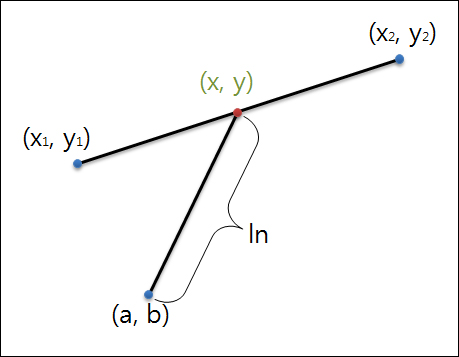
제목이 난해하니 먼저 그림부터 보였습니다. 주어진 선분이 있습니다. 이 선분의 시작점은 (X1, Y1)이고 끝점은 (X2, Y2)입니다. 그리고 주어진 좌표가 있으며 (a, b)입니다. 이 선분과 좌표에 대해서 거리 ln를 가지는 선분상의 좌표를 구하는 것에 대한 정리 포스트입니다. 즉, 위의 그림에서 파란색 점은 주어진 좌표이고 빨간 점을 구하겠다는 것입니다.
먼저 선분에 대한 아래와 같은 매개변수 방정식을 정합니다.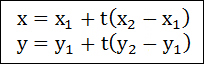
우리가 구해야할 점은 선분상의 점이니 위의 매개변수 방정식에서 x와 y가 바로 우리가 원하는 값입니다. 이 x와 y를 구하기 위해서는 매개변수 t를 구하면 됩니다. 아시겠지만 t가 주어진 선분위에 존재하려면 0~1사이의 값이여야 합니다. 이 값을 벗어나면 답은 없음… 입니다.
이 한가지 관계만 가지고는 않됩니다. 또 하나의 관계를 맺어줘야 합니다. 그 관계는 주어진 좌표(a, b)와 구하고자 하는 선분상의 점(x, y)사이의 거리가 값 ln이라는 사실로부터 다음과 같은 식을 얻을 수 있습니다.![]()
이제 처음 선분에 대한 방정식을 위의 방정식의 x, y에 대입하고 t에 대해 정리를 하면 아래와 같은 t에 대한 2차 방정식이 도출되며 이 2차 방정식을 근의 공식을 통해 t를 구해 보면 다음과 같습니다.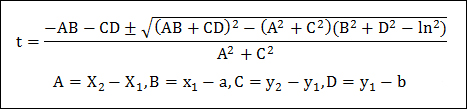
이렇게 구한 t에 대해서 범위가 0~1사이 인지를 검사하고 이 범위에 있다면 이 t를 선분의 방정식에 대입하여 구한 (x, y)가 구하고자 하는 좌표입니다.
타원의 방정식
이 얼마나 오랜만에 써보는 포스팅인지 모르겠습니다. 요즘 이러 저런 일로 바쁘다보니 블로그 관리에 매우 소홀했습니다. 이제 부터라도 짬짬히 시간을 내어.. 일상 업무에서 찾은 내용을 올리도록 노력 해야겠습니다. 해서… 알고보면 매우 간단한 내용이지만 포스팅 하나 올려봅니다.
오늘, 열심히 코드를 작성하던 중에.. 2차원에서 타원을 구성하는 좌표를 뽑아 낼 필요가 있었습니다. Needs는 하나의 타원과 또 다른 하나의 폴리곤을 하나의 도형으로 합(Union)하는 연산이 필요할듯 한데… 타원에 대한 정보는 단순히 중심점과 장반경 그리고 단반경만을 가지고 있음으로 폴리곤에 바로 합할 수 없는지라.. 일단 타원을 구성하는 정점을 이용하여 폴리곤으로 만들고.. 폴리곤과 폴리곤의 합 연산을 통해 원하는 결과를 얻고자 함이였습니다.
간단히 타원의 공식은 인터넷(http://en.wikipedia.org/wiki/Ellipse)을 통해 아래처럼 얻었습니다. 물론 프로그래밍에서 쉽게 사용할 수 있는 매개변수방정식으로 말입니다.
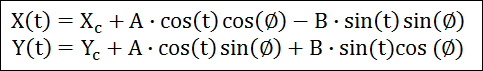
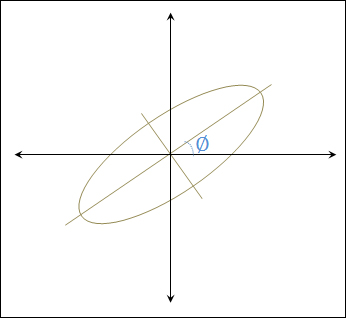
위의 식에서 Xc와 Yc는 타원의 중심입니다. 그리고 A와 B는 각각 X축과 Y축에 대한 타원의 반경이며 각각을 장축과 단축이라고 하겠습니다. 그리고 t는 0도에서 360도까지의 범위입니다. 물론 0도와 360도는 동일하므로 둘 중 하나는 포함되지 않아야 합니다. 마지막으로 ∅는 장축과 X축이 이루는 각도 입니다. 즉 ∅를 통해 기울어진 타원을 구성하는 좌표를 정의할 수가 있습니다. ∅에 대한 이해를 돕기 위해 아래 그림을 참고 하시기 바랍니다.
[GIS] 개발 맵 엔진의 Slope, Aspect, Hillshade
지형이라는 주제로 제작된 라스터(Raster)의 셀(Cell)에 기반한 분석 중 경사(Slope)와 향(Aspect) 분석은 중요한 자리를 차지하며, 이 경사와 향은 지형에 대한 분석 및 응용의 파라메터로 사용됩니다. 이 글은 개발 중인 지도 엔진의 확장 기능의 하나로써 경사와 향을 분석하는 것과 이 경사와 향을 분석하는 기능을 응용하여 다시 지형의 음영도(Hillshade)를 만드는 확장 기능에 대한 소개입니다. 여기서 확장 기능이란 지도 엔진과는 별개의 파일 단위로써 엔진에 플러그인하여 별도의 스레드를 통해 실행시킬 수 있는 외부의 확장 실행 단위 모듈입니다.
경사와 향 값을 분석하기 위해서는 분석 대상이 되는 지역에 대한 DEM 데이터가 필요합니다. 이 DEM의 라스터 데이터로써 아래와 같은 데이터를 사용하였습니다.
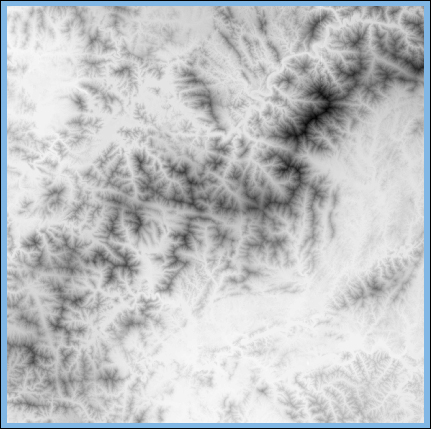
이 데이터는 김한국님이 운영하는 비지니스 GIS 커뮤니티(www.biz-gis.com)에서 내려 받은 데이터입니다. 그리고 위의 이미지를 포함해서 앞으로 나오는 지도 화면은 모두 오픈메이트(www.openmate.co.kr)의 개발한 맵 엔진으로 생성한 화면입니다. 위의 데이터를 통해 경사값과 향을 계산하기 전에 간단히 경사와 향이 무엇인지에 대해 언급하겠습니다.
경사(Slope)란 어떤 지점의 지반이 수평을 기준으로 몇도 정도 기울어져 있는가를 말하는 것으로 다음 그림을 통해 쉽게 이해할 수 있을 것입니다.
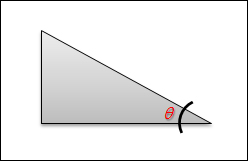
바로 저 세타 각도가 경사 기울기에 대한 각도로써 각이 클 수록 지반의 경사가 급하고 각이 0이면 평편한 지반임을 나타냅니다.
향(Aspect)이란 지반의 경사면이 어디를 향하고 있는지에 대한 것입니다. 만약 지반의 경사면이 북쪽을 향하고 있다면 0도, 동쪽은 90도, 남쪽은 180도 그리고 서쪽은 270도가 됩니다. 완전히 평편할 경우 GIS 시스템마다 다른 값을 주게 되는데, 여기서는 Null 값을 줍니다. (사실 Null은 값이 없다는 의미이므로, 좀더 정화하게 한다면 0~360이 아닌 다른 값을 주어야 옳습니다. 예를들어서 -1과 같은 값이 적당하겠습니다)
실제로 구현된 경사와 향에 대한 실행 결과는 아래와 같습니다. 각각 경사와 향에 대한 이미지입니다.

가만이 보면 향의 분석 결과가 불완전하기는 하지만 음영기복도(Hillshade)와 비슷해 보입니다. 여기서 Hillshade는 태양광의 위치를 정해주면 태양광의 영향으로 지형 데이터를 입체감 있게 표현해 주는 방법입니다. 아래는 이러한 내용으로 개발한 맵 엔진에 구현된 Hillshade의 결과입니다.

태양의 위치는 북동쪽(270)이고 고도는 45도로 정했습니다. 위의 Hillshade의 결과는 비록 입체적으로 보이기는 하지만 마치 석고를 발라 놓은 듯이 매우 딱딱해 보입니다. 이를 좀더 예술적(?)으로 표현하기 위해 이 글의 가장 처음 보여드렸던 지형 데이터의 원본 이미지와 위의 Hillshade를 합성하게 되는데, 좀더 멋진 음영기복도를 위한 합성 방법은 Hillshade을 약간 투명하게 하고 Luminosity 방식으로 합성해야 하나, 개발한 맵 엔진에서는 Luminosity 방식의 합성을 지원하지 않아 그냥 투명도만 주어 새롭게 음영기복도를 만들어 보았습니다. 그 결과는 아래와 같습니다.

봄 계절에 맞게 색상을 넣어 보았습니다. 좀더 색상을 다체롭게 넣는다면 더 멋진 음영기복도 만들어 질 것으로 판단되며, 앞서 언급한 Luminosity 합성을 사용하면 보다 분명한 음영기복도가 만들어 질 것 입니다. 이상으로 개발한 맵 엔진에서 확장기능으로 개발한 경사, 향 그리고 Hillshade에 대한 소개를 마칩니다.
[GIS] IDW(Inverse Distance Weighting)
IDW는 이미 알고 있는 값으로부터 알고자 하는 값을 보간하는 방법입니다. IDW를 사용하여 주어진 점 x에 대한 보간된 값 u를 결정하는 일반화된 형태의 보간 함수는 다음과 같습니다.
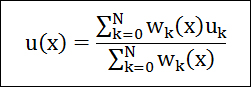
N은 이미 알고 있는 값의 개수, w는 가중치의 값, u는 앞서 말한 계산되어 나온 보간된 값입니다. IDW에서 중요한것은 가중치의 값에 해당되는 w에 대한 함수가 여러개 존재하며, Spepard 방식과 Liszka 방식 그리고 이들의 변종이 존재합니다. 여기서는 Spepard 방식에 대한 w값에 대해서만 살펴 보겠습니다.
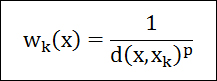
위의 식이 Spepard님이 정의한 가중치 w의 값입니다. d는 보간하고자 하는 지점(x)와 이미 알고 있는 지점(xk) 사이의 공간적 거리입니다. 바로 거리(Distance)의 역(Inverse)에 대한 가중치(Weighting)라는 의미로 IDW가 된 것입니다.
p는 0보다 큰 실수값입니다. 이 p값의 범위에 따라 전체적인 보간된 양상이 다양하게 결정됩니다. p의 범위가 0~1이면 전체적인 양상이 좁고 날카로우며 1보다 크면 넓고 부드럽게 퍼져서 보간이 됩니다. 눈에 보이는 보간된 양상을 글로써 표현하려니 한계가 있는데… 이 부분에 대해서 실제 구현을 통해 살펴보도록 하겠습니다.
끝으로 IDW처럼, 이미 알고 있는 값을 통해 다른 값을 추정(보간)하는 방법 중 Kriging 기법이 있습니다. 기회가 닿는 다면 이 Kriging 기법에 대해서도 논의해 보고 싶습니다.
보간 – Catmull-Rom Spline
많은 스플라인의 종류 중에 하나인 큐빅 스플라인을 1차원의 보간에 적용하는 것에 대해 살펴보겠습니다. Catmull-Rom 스플라인을 구성하는 구분된 부드러운 곡선들을 나타내는 키 프레임 집합을 가지며 모든 키는 곡선 상에 위치합니다. 이 루틴을 사용하기 위해서 4개의 키 프레임 값이 필요합니다. 이 4개의 키 값을 v0, v1, v2, v3라고 하고, 여기에 보간을 위하여 v1에서 v2 사이의 지정된 0~1까지의 범위를 가지는 실수값 x가 존재합니다. 아래의 f(x)의 반환값은 x값에 의해 결정이 됩니다.
![]()
여기서 M은 다음처럼 정의됩니다.
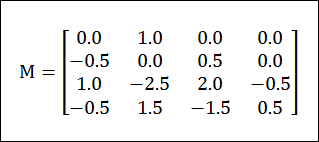
아래의 이미지는 v1에서 v2 사이의 곡선의 한 예를 나타난 것입니다. 이 곡선은 위의 수식에서 x 값을 0에서 1.0 사이의 값을 이용해 얻을 수 있습니다.
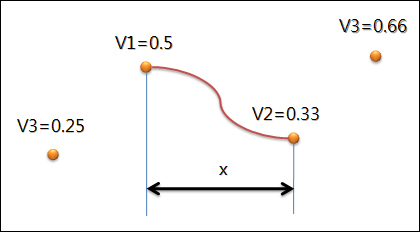
아래의 코드는 위에서 설명한 내용을 C언어로 구현한 것입니다.
/* Coefficients for Matrix M */
#define M11 0.0
#define M12 1.0
#define M13 0.0
#define M14 0.0
#define M21 -0.5
#define M22 0.0
#define M23 0.5
#define M24 0.0
#define M31 1.0
#define M32 -2.5
#define M33 2.0
#define M34 -0.5
#define M41 -0.5
#define M42 1.5
#define M43 -1.5
#define M44 0.5
double catmullRomSpline(float x, float v0,float v1, float v2,float v3) {
double c1,c2,c3,c4;
c1 = M12*v1;
c2 = M21*v0 + M23*v2;
c3 = M31*v0 + M32*v1 + M33*v2 + M34*v3;
c4 = M41*v0 + M42*v1 + M43*v2 + M44*v3;
return(((c4*x + c3)*x +c2)*x + c1);
}
이 글의 원문은 http://www.lighthouse3d.com/opengl/maths/index.php?catmullrom 입니다.

