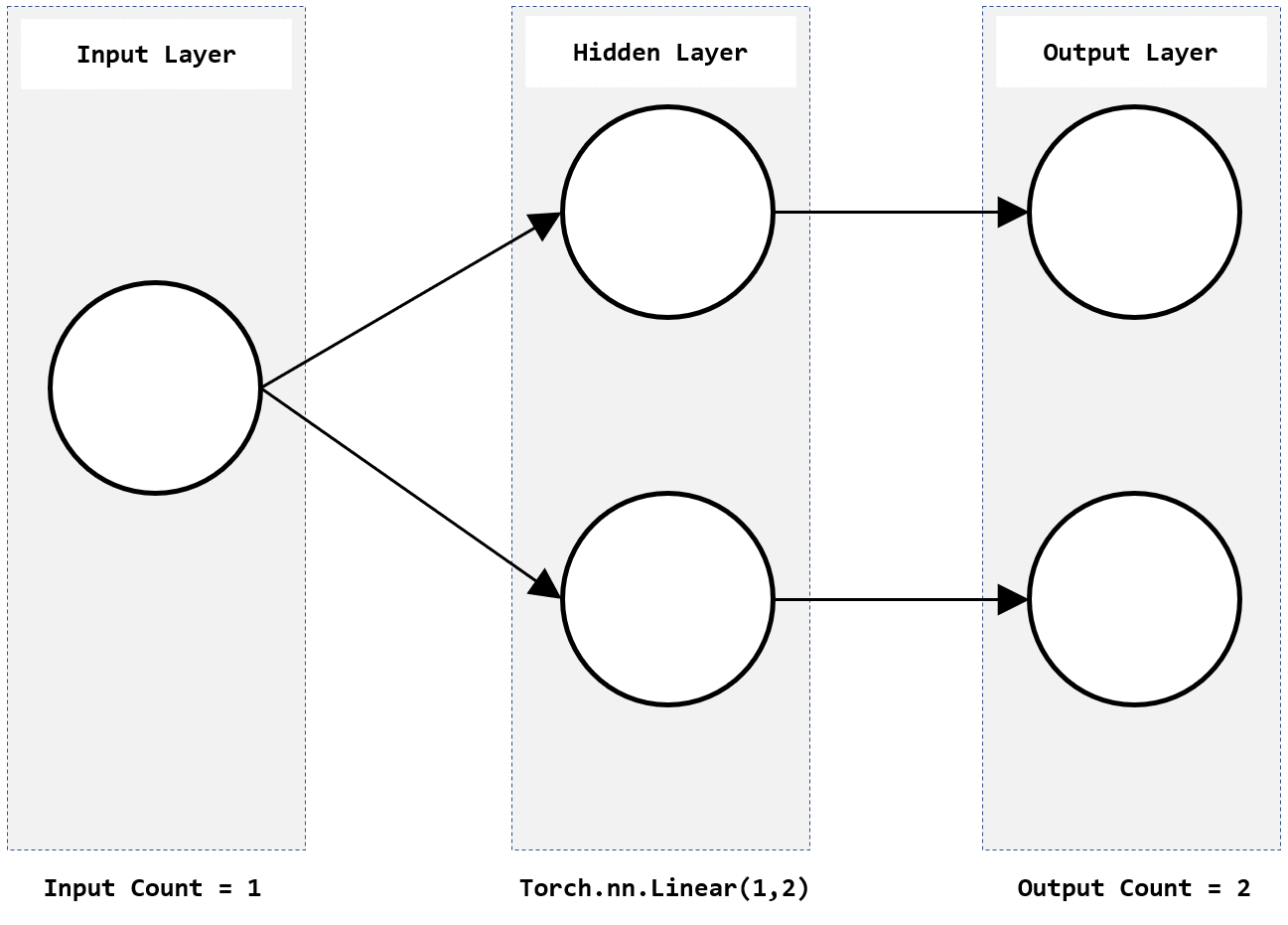
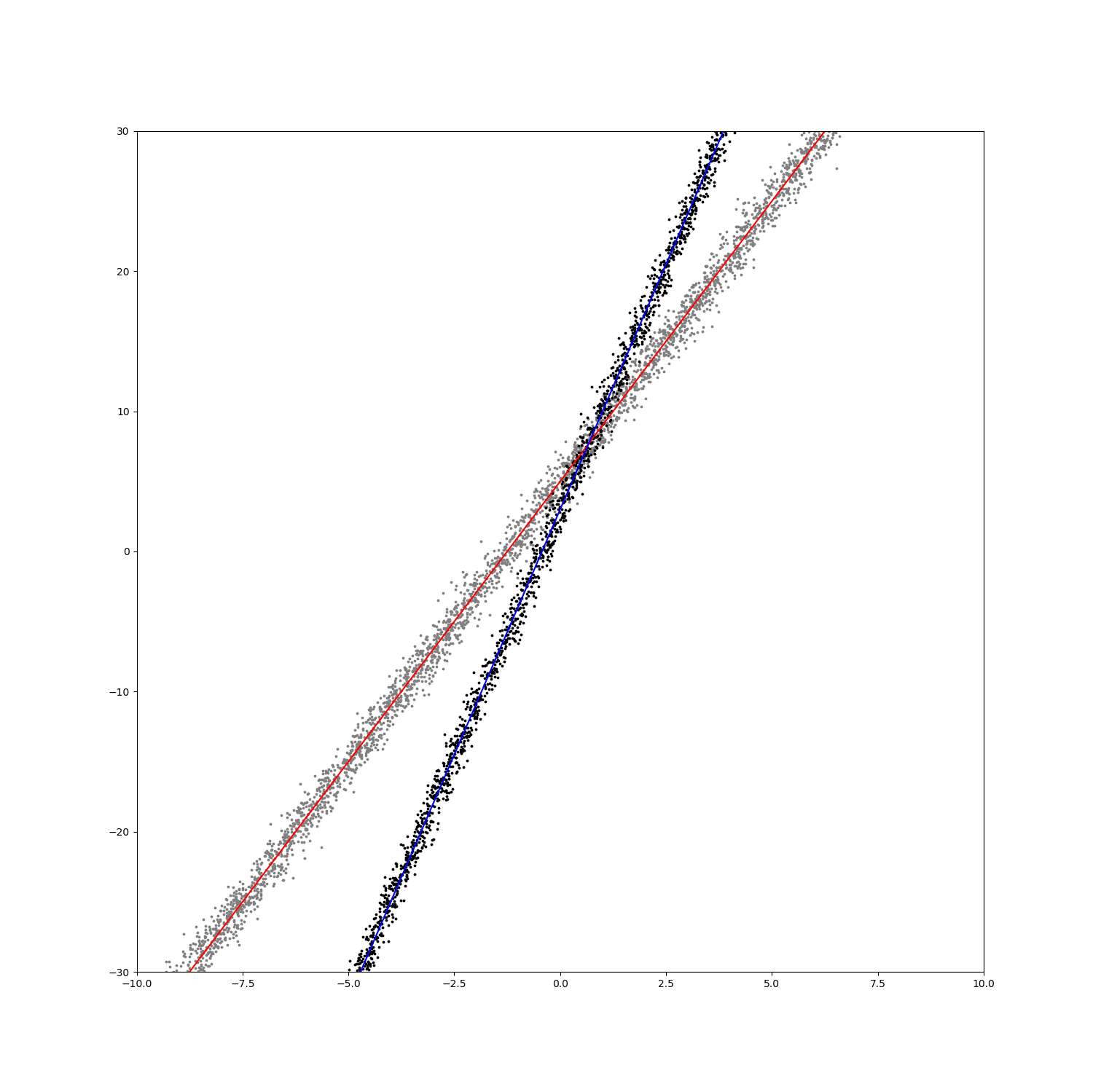
NumPy는 직관적이지만 때로는 축약적인 표현식과 함축적인 코드 안에 내포된 의미의 파악이 명확하게 그려지지 않는 경우가 있습니다. 물론 NumPy의 축약된 표현식과 그 함축적인 의미는 그 전체가 기본과 기본들의 연결로 완성된 것이기에 기본적인 내용을 더 중요시하여 기록해 둡니다.
#0. 배열 생성
import numpy as np
a = np.empty([3, 3])
print(a)
b = np.random.randn(3,3)
print(b)
a와 b는 모두 3×3 행렬입니다. 차이점을 보면, 먼저 a는 초기화없이 행렬을 생성하므로, a의 요소값은 어떠한 규칙성이 없으며 b는 정규분포에 따라 행렬의 원소값을 초기화합니다.
#1. 배열로 생성
import numpy as np
x = np.array([1., 2., 3., 4.])
print(x) # output: [1. 2. 3. 4.]
print(type(x)) # output: <'numpy.ndarray'>
print(x.shape) # output: (4,)
print(np.ndim(x)) # output: 1
y = np.array([
[1., 2., 3., 4.],
[9., 8., 7., 5.]
])
print(y.shape) # output: (2, 4)
print(np.ndim(y)) # output: 2
#2. 원소의 접근
x = np.array([
[1, 2, 3],
[4, 5, 6]
])
print(x[0]) # output: [1 2 3]
print(x[0][0]) # output: 1
print(x[0][0] == x[0,0]) # output: True
for r in x:
print(r)
# output:
# [1 2 3]
# [4 5 6]
#3. 산술 연산
numpy.ndarray 타입 객체 간의 산술연산(+, -, *, /)는 원소별(element-wise product)입니다. +, -, *, / 산술연산에 대한 동일한 매서드는 각각 np.add, np.subtract, np.multiply, np.divide 입니다.
a = np.array([10,20,30])
b = np.array([1,2,3])
print(a+b) # output: [11 22 33]
print(a-b) # output: [ 9 18 27]
print(a*b) # output: [10 40 90]
print(a/b) # output: [10. 10. 10.]
numpy.ndarray과 단일값(Scalar)에 대한 산술 연산은 보로드케스트(Boradcast) 처리됩니다.
a = np.array([10,20,30])
b = 100
print(a+b) # output: [110 120 130]
print(a-b) # output: [-90 -80 -70]
print(a*b) # output: [1000 2000 3000]
print(a/b) # output: [0.1 0.2 0.3]
특정 위치에 대해 특정값을 더할 수 있는 np.add.at 이라는 함수가 있는데, 그 예는 다음과 같습니다.
import numpy as np
a = np.arange(20).reshape(5,4)
b = np.arange(4)
print(a)
''' output:
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]
[12 13 14 15]
[16 17 18 19]]
'''
print(b) # [0 1 2 3]
np.add.at(a, 1, b)
print(a)
''' output:
[[ 0 1 2 3]
[ 4 6 8 10]
[ 8 9 10 11]
[12 13 14 15]
[16 17 18 19]]
'''
np.add.at(A, idx, B)는 B를 A의 idx 번째 행에 더하는 연산입니다.
#4. 브로드케스트
스칼라뿐만 아니라 shape가 다른 배열 간에도 브로드케스트로 처리됩니다.
a = np.array([
[1, 2],
[3, 4],
])
b = np.array([
[100],
[200]
])
c = np.array([
[100, 200]
])
print(a+b)
# output:
# [[101 102]
# [203 204]]
print(a+c)
# output:
# [[101 202]
# [103 204]]
#5. 행렬의 곱(내적) 연산
import numpy as np
a = np.array([
[1, 2],
[3, 4]
])
b = np.array([
[5, 6],
[7, 8]
])
c = np.dot(a, b)
print(c)
# output:
# [[19 22]
# [43 50]]
#6. 배열 요소의 합과 곱
a = np.array([1., 2., 3.])
print(np.sum(a)) # output: 6.0 (1 + 2 + 3)
print(np.prod(z)) # output: 6.0 (1 * 2 * 3)
z = np.array([True, False, True, False])
print(np.sum(z)) # output: 2
True는 1로, False 0으로 변환되어 합산됩니다.
#7. 배열 요소 중 최대값의 인덱스 구하기
import numpy as np
x = np.array([
[0.1, 0.8, 0.1],
[0.3, 0.1, 0.6],
[0.2, 0.5, 0.3],
[0.8, 0.1, 0.1]
])
y = np.argmax(x)
y0 = np.argmax(x, axis=0)
y1 = np.argmax(x, axis=1)
print(y) # output: 1
print(y0) # output: [3 0 1]
print(y1) # output: [1 2 1 0]
np.argmax(x)는 x 배열을 1차원으로 평면화된 배열에 대해 최대값을 갖는 인덱스를 반환하고, np.argmax(x, axis=0)는 첫번째 축인 row 방향(세로방향)으로 구성되는 요소 중 최대인 인덱스를 반환하며, y1 = np.argmax(x, axis=1)는 두번째 축인 column 방향(가로방향)으로 구성되는 요소 중 최대인 인덱스를 반환합니다.
#8. 배열 요소 중 임의로 몇 개만 뽑아내기
기계학습이나 신경망 훈련 때 방대한 입력 데이터 중 일부만을 뽑아내 활용해야 하는 경우가 있는데, 이를 위한 코드입니다. 아래는 총 9개의 요소 중 3개의 요소를 임의로 뽑아내 배열로 반환합니다.
import numpy as np
a = [10,20,30,40,50,60,70,80,90]
n = np.array(a)
i = np.random.choice(n.shape[0], 3)
print(i) # output: [6 5 3]
s = n[i]
print(s) # output: [70 60 40]
위의 예에서 요소의 선택되는 기준은 동일합니다. 이와 대조적으로 요소를 선택하는 기준에 대해, 각 요소가 선택될 확률을 지정할 수 있습니다. 아래의 예가 바로 그것입니다.
import numpy as np
n = np.array([10,20,30,40,50,60,70,80,90])
p = np.array([ 0, 0, 0, 0, 1, 0, 0, 0, 0])
i = np.random.choice(n.shape[0], 3, p=p)
print(i) # output: [4 4 4]
s = n[i]
print(s) # output: [50 50 50]
항상 요소 50만 선택되는데, 이유는 50요소에 대한 선택확률을 1(100%)로 지정하고, 나머지는 0(0%)로 지정했기 때문입니다.
#9. 배열 요소의 형변환
import numpy as np
a = np.array([-1.0, 1.0, 2.0])
b = a > 0.0
c = b.astype(np.int)
print(b) # output: [False True True]
print(c) # output: [0 1 1]
아래처럼 배열을 생성할 때 타입을 강제로 지정할 수도 있습니다.
import numpy as np
a = np.array([-1.0, 1.0, 2.0])
b = np.array(a > 0.0, dtype=np.int)
print(b) # output: [0 1 1]
#10. Masking 연산
요소 타입이 boolean인 조건 배열을 이용해서 원하는 위치의 요소값만 변경하는 마스킹 연산입니다.
import numpy as np
a = np.arange(0, 16)
b = a.reshape(4,4)
c = b > 8
b[c] = 0
c와 b는 각각 아래와 같습니다.
a = [ [False False False False]
[False False False False]
[False True True True]
[ True True True True] ]
b = [ [0 1 2 3]
[4 5 6 7]
[8 0 0 0]
[0 0 0 0] ]
#11. 배열 요소의 최대, 최소, 합, 평균 구하기
import numpy as np
a = np.arange(0, 16).reshape(4,4)
'''
a = [[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]
[12 13 14 15]]
'''
max = np.max(a) # = 15
min = np.min(a) # = 0
sum = np.sum(a) # = 120
mean = np.mean(a) # = 7.5
축(axis)에 대한 연산의 예는 다음과 같습니다.
import numpy as np
a = np.arange(0, 16).reshape(4,4)
max = np.max(a, axis=0) # = [12 13 14 15]
min = np.min(a, axis=0) # = [0 1 2 3]
sum = np.sum(a, axis=0) # = [24 28 32 36]
mean = np.mean(a, axis=0) # = [6. 7. 8. 9.]
Numpy의 axis에 대한 이해를 돕는 글은 아래를 참고하기 바랍니다.
Numpy의 axis에 따른 연산
#12. 주어진 범위에서 일정한 간격으로 배열 만들기
예를들어, 0부터 10까지 순차적으로 3개의 요소로 구성된 배열을 생성하고자 한다면..
import numpy as np
a = np.linspace(0, 10, 3) # = [ 0. 5. 10.]
#13. 중복되는 요소 제거하기
배열 요소 중 유일한 값만으로 구성하기 위한 내용입니다.
import numpy as np
a = np.array([1,2,2,3,4,2,4,5,6,7,6])
b = np.unique(a) # = [1 2 3 4 5 6 7]
#14. 인덱스 리스트를 통한 특정 원소 값 얻기(Fany Indexing)
배열에 대한 다수의 인덱스를 리스트로 지정하고, 해당 인덱스의 값을 얻는 내용입니다.
import numpy as np
matrix = np.array([
[ 1, 2, 3 ],
[ 4, 5, 6 ],
[ 7, 8, 9 ]
])
# (0,1)과 (2,0)의 위치에 대한 값을 출력
print(matrix[[0,2],[1,0]]) # = [2 7]
#15. 2차원 배열을 1차원 배열로 만들기
import numpy as np
a = np.array([
[ 1, 2, 3, 4 ],
[ 4, 5, 6, 7 ],
[ 7, 8, 9, 1 ]
])
print(a.reshape(12)) # = [1 2 3 4 4 5 6 7 7 8 9 1], 참조
print(a.reshape(-1)) # = [1 2 3 4 4 5 6 7 7 8 9 1], 참조
print(a.ravel()) # = [1 2 3 4 4 5 6 7 7 8 9 1], 참조
print(a.flatten()) # = [1 2 3 4 4 5 6 7 7 8 9 1], 복사
#16. 전치행렬 및 행렬식 구하기
전치행렬은 행과 열의 위치가 서로 바뀐 행렬이며, 행렬식은 정방행렬에 대해서만 구할 수 있으며 선형 변환의 특징을 나타내는 스칼라값입니다.
import numpy as np
a = np.array([
[ 1, 2, 3 ],
[ 2, 4, 6 ],
[ 3, 8, 9 ]
])
print(np.linalg.det(a))
print(a.T)
#17. 대각행렬을 뽑아내거나, 대각 행렬 만들기
행렬의 대각 성분만을 뽑아내는 코드는 다음과 같습니다.
import numpy as np
a = np.array([
[ 1, 2, 3 ],
[ 2, 4, 6 ],
[ 3, 8, 9 ]
])
print(a.diagonal(offset=0)) # = [1 4 9]
offset의 기본값은 0이며, 이 값을 조정하여 뽑아낼 대각성분의 위치를 조정할 수 있습니다. np.diag(a) 역시 동일한 기능인데, a가 1차원 배열일 때 a를 대각성분으로 하는 행렬을 만듭니다.
import numpy as np
a = np.array([1, 2, 3])
print(np.diag(a))
'''
= [[1 0 0]
[0 2 0]
[0 0 3]]
'''
#18. 인덱스값을 담은 배열로 다른 배열의 요소값 뽑아내기
import numpy as np
W = np.arange(21).reshape(7, 3)
print(W)
''' output:
[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]
[12 13 14]
[15 16 17]
[18 19 20]]
'''
idx = np.array([1,0])
print(W[idx])
''' output:
[[3 4 5]
[0 1 2]]
'''
#19. 배열의 요소값 이산화
import numpy as np
a = np.array([1,2,3,4,5,6,7,8])
b = np.digitize(a, bins=[3,6])
print(b) # = [0 0 1 1 1 2 2 2]
위의 예는 [최소,3), [3,6), [6,최대] 구간에 포함되는 요소를 각각 0, 1, 2로 이산화시킵니다. np.digitize 함수의 인자 중 right=True로 지정하면 이산화를 위한 구간을 [최소,3], (3,6], (6,최대]으로 변경됩니다.
#20. 배열 요소 전체에 대한 지정 표현(…)
import numpy as np
a = np.empty((3,3,3))
print('a =',a)
'''Output:
a = [[[-2.82281278e+170 1.08844231e-311 6.95255452e-310]
[ 1.12941561e+028 1.08844231e-311 6.95255452e-310]
[-1.23638776e+273 1.08844231e-311 6.95255452e-310]]
[[ 1.82340557e-026 1.08844231e-311 6.95255452e-310]
[-1.08726484e+173 -1.68404675e-310 6.95255452e-310]
[-9.41689305e-154 1.08844231e-311 6.95255452e-310]]
[[-6.02914348e-006 1.08844231e-311 6.95255452e-310]
[-4.46357303e-063 1.08844231e-311 6.95255452e-310]
[ 1.70128236e+132 1.08844232e-311 6.95255452e-310]]]
'''
print('a[...] =',a[...])
'''Output:
a = [[[-2.82281278e+170 1.08844231e-311 6.95255452e-310]
[ 1.12941561e+028 1.08844231e-311 6.95255452e-310]
[-1.23638776e+273 1.08844231e-311 6.95255452e-310]]
[[ 1.82340557e-026 1.08844231e-311 6.95255452e-310]
[-1.08726484e+173 -1.68404675e-310 6.95255452e-310]
[-9.41689305e-154 1.08844231e-311 6.95255452e-310]]
[[-6.02914348e-006 1.08844231e-311 6.95255452e-310]
[-4.46357303e-063 1.08844231e-311 6.95255452e-310]
[ 1.70128236e+132 1.08844232e-311 6.95255452e-310]]]
'''
print('a[0,...] =',a[0,...])
'''Output:
a[0,...] = [[-2.82281278e+170 1.08844231e-311 6.95255452e-310]
[ 1.12941561e+028 1.08844231e-311 6.95255452e-310]
[-1.23638776e+273 1.08844231e-311 6.95255452e-310]]
'''
print('a[0,0,...] =',a[0,0,...])
'''Output:
a[0,0,...] = [-2.82281278e+170 1.08844231e-311 6.95255452e-310]
'''
print('a[0,0,0] =',a[0,0,0])
'''Output:
a[0,0,0] = -2.8228127844826624e+170
'''
#21. NaN 값 삭제하기
import numpy as np
a = np.array(
[
[1, 2],
[3, 4],
[np.nan,4],
[2,np.nan],
[4, 5]
]
)
b = a[~np.isnan(a).any(axis=1)]
print(b)
'''Output:
[[1. 2.]
[3. 4.]
[4. 5.]]
'''
#22. 특정한 값 대체하기
예를들어, 배열 요소 중에 값이 2인 항목을 100으로 변경하고자 한다면 다음 코드의 예와 같습니다.
import numpy as np
X = np.array(
[
[0, 1, 1],
[1, 2, 3],
[2, 3, 5],
[3, 2, 1],
[4, 1, 6],
]
)
X = np.where(X==2, 100, X)
print(X)
''' Output:
[[ 0 1 1]
[ 1 100 3]
[100 3 5]
[ 3 100 1]
[ 4 1 6]]
'''
#23. 두 배열을 합치기
여기서 소개할 배열을 합치는 넘파이의 함수에는 3가지로, vstack, hstack, concatenate가 있습니다. vstack은 Vertical Stack으로 수직방향으로 쌓아 합치는 것이고, hstack은 Horizontal Stack으로 수평방향으로 쌓아 합치는 것입니다. 그리고 concatenate은 합치고자 하는 배열에 맞게 합치는 것입니다. 구체적인 내용은 아래의 예제 코드를 통해 명확하게 확인할 수 있습니다.
import numpy as np
X = np.array(
[
[0, 1, 2],
[3, 4, 5],
[6, 7, 8]
]
)
Y = np.array(
[
[100, 101, 102],
[103, 104, 105],
[106, 107, 108]
]
)
V = np.vstack((X, Y))
print(V)
'''Output:
[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[100 101 102]
[103 104 105]
[106 107 108]]
'''
H = np.hstack((X, Y))
print(H)
'''Output:
[[ 0 1 2 100 101 102]
[ 3 4 5 103 104 105]
[ 6 7 8 106 107 108]]
'''
C = np.concatenate((X, Y))
print(C)
'''Output
[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[100 101 102]
[103 104 105]
[106 107 108]]
'''
concatenate에 대해 좀더 구체적으로 파악하기 위해 다음 예를 들어봅니다.
import numpy as np
X = np.array([0,1,2])
Y = np.array([100,101,102])
C = np.concatenate((X, Y))
print(C)
'''Output:
[ 0 1 2 100 101 102]
'''
X = np.array([[0],[1],[2]])
Y = np.array([[100],[101],[102]])
C = np.concatenate((X, Y))
print(C)
'''Output:
[[ 0]
[ 1]
[ 2]
[100]
[101]
[102]]
'''
#24. 배열 요소 뒤집기
배열을 구성하고 있는 요소들의 구성 순서를 뒤집고자 하는 경우에 대한 예입니다. 먼저 간단이 1차원 배열에 대한 경우입니다.
import numpy as np
A = np.array([0,1,2,3,4,5,6,7,8,9])
AR = A[::-1]
print(AR) # = [9 8 7 6 5 4 3 2 1 0]
이제 2차원 배열에 대해 살펴보면, 먼저 Row 벡터를 단위로 뒤집는 코드입니다.
import numpy as np
B = np.array(
[
[0,1,2,3,4],
[1,2,3,4,5],
[2,3,4,5,6],
[3,4,5,6,7]
]
)
BR = B[::-1]
print(BR)
'''Output:
[[3 4 5 6 7]
[2 3 4 5 6]
[1 2 3 4 5]
[0 1 2 3 4]]
'''
다음은 Row 벡터를 구성하는 요소들을 뒤집는 코드입니다.
import numpy as np
B = np.array(
[
[0,1,2,3,4],
[1,2,3,4,5],
[2,3,4,5,6],
[3,4,5,6,7]
]
)
BR = B[...,::-1]
print(BR)
'''Output:
[[4 3 2 1 0]
[5 4 3 2 1]
[6 5 4 3 2]
[7 6 5 4 3]]
'''
다음은 Row 벡터를 단위로 뒤집음과 동시에 Row 벡터를 구성하는 요소도 뒤집는 코드입니다.
import numpy as np
B = np.array(
[
[0,1,2,3,4],
[1,2,3,4,5],
[2,3,4,5,6],
[3,4,5,6,7]
]
)
BR = B[...,::-1][::-1]
print(BR)
'''Output:
[[7 6 5 4 3]
[6 5 4 3 2]
[5 4 3 2 1]
[4 3 2 1 0]]
'''
#25. numpy.flip 함수를 이용한 배열 요소 뒤집기
flip 함수를 통해 좀더 쉽고 직관적으로 배열 요소를 뒤집을 수 있습니다. 3차원 이상의 배열에 대해서 뒤집을때 좀더 직관적입니다. 코드는 아래와 같습니다.
import numpy as np
B = np.array(
[
[0,1,2,3,4],
[1,2,3,4,5],
[2,3,4,5,6],
[3,4,5,6,7]
]
)
print(np.flip(B,0)) # 축(Axis) 0에 대해 뒤집기
'''output:
[[3 4 5 6 7]
[2 3 4 5 6]
[1 2 3 4 5]
[0 1 2 3 4]]
'''
print(np.flip(B,1)) # 축 1에 대해 뒤집기
'''output:
[[4 3 2 1 0]
[5 4 3 2 1]
[6 5 4 3 2]
[7 6 5 4 3]]
'''
print(np.flip(B)) # 모든 축에 대해 뒤집기 아래의 코드와 동일함
print(np.flip(B, (0, 1)))
'''output:
[[7 6 5 4 3]
[6 5 4 3 2]
[5 4 3 2 1]
[4 3 2 1 0]]
'''
#26. 어떤 배열로부터 원하는 데이터를 뽑아내 새로운 배열 구성하기
import numpy as np
A = np.array(
[
[0,1,2,3,4],
[1,2,3,4,5],
[2,3,4,5,6],
[3,4,5,6,7]
]
)
B = A[..., [0,2]]
print(B)
'''output:
[[0 2]
[1 3]
[2 4]
[3 5]]
'''
C = A[[0,2], ...]
print(C)
'''output:
[[0 1 2 3 4]
[2 3 4 5 6]]
'''
B는 A에 대해서 열(Column) 인덱스 0, 2에 대한 데이터만을 뽑아낸 배열이고, C는 A에 대해서 행(Row) 인덱스 0, 2에 대한 데이터만을 뽑아낸 배열입니다.
#27. 배열 요소의 반복
Numpy의 repeat 함수는 3개의 인자를 받습니다. 첫번째는 반복하고자 하는 데이터이고, 두번째는 반복 횟수이며 세번째는 반복하고자 하는 축(Axis)로 선택 인자입니다.
import numpy as np
a = np.repeat(3, 4)
print(a) # Output: [3 3 3 3]
x = np.array(
[
[1, 2],
[3, 4]
]
)
b = np.repeat(x, 2)
print(b) # Output: [1 1 2 2 3 3 4 4]
c = np.repeat(x, 3, axis=1)
print(c)
''' Output:
[[1 1 1 2 2 2]
[3 3 3 4 4 4]]
'''
d = np.repeat(x, 3, axis=0)
print(d)
''' Output:
[[1 2]
[1 2]
[1 2]
[3 4]
[3 4]
[3 4]]
'''
e = np.repeat(x, [1, 2], axis=0)
print(e)
''' Output:
[[1 2]
[3 4]
[3 4]]
'''
f = np.repeat(x, [1, 2], axis=1)
print(f)
''' Output:
[[1 2 2]
[3 4 4]
'''
#28. 두 배열간의 대소 비교
두 배열의 구성 요소에 대해 동일한 위치의 요소에 대한 크거나 작은지에 대한 비교를 위한 예제입니다.
import numpy as np
a = np.greater([4,2], [2,2])
print(a) # [True, False]
geater 함수 이외에도 다양한 비교를 위해 greater_equal, less, less_equal, equal, not_equal 함수가 제공됩니다.
#29. 배열 요소값의 최소값 조정하기
배열을 구성하는 요소값을 특정한 값 이하일 경우 그 특종한 값으로 변경하는 코드입니다.
import numpy as np
a = np.array([
[1,2,3],
[4,5,6],
[7,8,9],
])
b = np.maximum(a, 5)
print(b)
''' Output:
[[5 5 5]
[5 5 6]
[7 8 9]]
'''
#30. 주어진 범위의 값(0이상의 정수)을 무작위 섞어 반환
0~9까지의 값을 무작위로 섞어 반환하는 코드의 예입니다.
import numpy as np
a = np.random.permutation(10)
print(a) # [6 8 5 7 3 2 1 4 0 9]
np.random.permutation 함수를 사용했으며, 인자는 범위 값의 구성 갯수입니다. 주로 인덱스값을 섞는 용도로 활용됩니다.
#31. 두 배열을 합치는 또 다른 방식
import numpy as np
a = np.array([1, 2])
b = np.array([3, 4])
c = np.c_[a,b]
print(c)
''' output:
[[1 3]
[2 4]]
'''
vs = np.vstack([a,b])
print(vs)
''' output:
[[1 2]
[3 4]]
'''
r = np.r_[a,b]
print(r)
''' output:
[1 2 3 4]
'''
hs = np.hstack([a,b])
print(hs)
''' output:
[1 2 3 4]
'''
a = np.array([[1, 2],
[3, 4]])
b = np.array([[5, 6],
[7, 8]])
c = np.c_[a,b]
print(c)
''' output:
[[1 2 5 6]
[3 4 7 8]]
'''
vs = np.vstack([a,b])
print(vs)
''' output:
[[1 2]
[3 4]
[5 6]
[7 8]]
'''
r = np.r_[a,b]
print(r)
''' output:
[[1 2]
[3 4]
[5 6]
[7 8]]
'''
hs = np.hstack([a,b])
print(hs)
''' output:
[[1 2 5 6]
[3 4 7 8]]
'''
#32. 차원 확장
원하는 축(Axis)에 대한 차원 확장을 위한 np.expand_dims 함수 예입니다.
import numpy as np
x = np.array(
[
[1, 2, 3],
[4, 5, 6],
]
)
z = np.expand_dims(x, axis=0)
print(z)
''' output
[[[1 2 3]
[4 5 6]]]
'''
t = x.reshape(-1,x.shape[0],x.shape[1])
print(t)
''' output
[[[1 2 3]
[4 5 6]]]
'''
위의 예를 보면, 많은 경우 reshape을 통해 np.expand_dims를 대신할 수 있음을 알 수 있습니다.
#33. 특정 값을 가지는 요소 인덱스 얻기
배열을 구성하는 어떤 값을 가지는 요소의 인덱스를 얻기 위한 np.argwhere 함수입니다.
import numpy as np
a = np.array([3, 2, 1, 5, 9, 8, 4, 5, 6, 7])
print(np.argwhere(a == 5))
''' output:
[[3]
[7]]
'''
이 함수는 조건을 만족하는 항목의 인덱스를 반환하는데, 아래는 2차원 구조일 경우에 대한 예입니다.
import numpy as np
z = np.arange(16).reshape(4,4)
print(z)
''' output:
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]
[12 13 14 15]]
'''
print(z%3==0)
''' output:
[[ True False False True]
[False False True False]
[False True False False]
[ True False False True]]
'''
print(np.argwhere(z%3==0))
''' output:
[[0 0]
[0 3]
[1 2]
[2 1]
[3 0]
[3 3]]
'''
위의 결과에서 보는 것처럼, 조건을 만족하는 항목에 대한 2차원 배열에서의 인덱스를 결과로 반환합니다.
#34. 배열을 가로 방향으로 잘라 재구성하기
예를들어, 4×4 행렬이 있다고 할때 이를 4×2 행렬 2개로 나눠 재구성하고자 할때 hsplit 함수를 사용합니다.
import numpy as np
a = np.arange(16).reshape(4,4)
print(a)
''' output
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]
[12 13 14 15]]
'''
b = np.hsplit(a,2)
print(b)
''' output
[array([[ 0, 1],
[ 4, 5],
[ 8, 9],
[12, 13]]),
array([[ 2, 3],
[ 6, 7],
[10, 11],
[14, 15]])]
'''
#35. 배열 요소들의 순차적 누적값 계산하기
배열을 구성하는 요소들을 계속 누적한 그 결과를 얻기 위해 numpy의 cumsum 함수를 사용하며, 예제는 다음과 같습니다.
import numpy as np
a = np.array([[1, 2, 3], [4, 5, 6]])
print(np.cumsum(a))
''' output
[ 1 3 6 10 15 21]
'''
cumsum 함수의 결과에는 입력 배열의 차원이 무시되어 1차원으로 반환됩니다.