[카테고리:] 미분류

티베로(Tibero)는 티맥스소프트의 자회사인 티맥스데이터에서 개발한 DBMS이다. 2003년에 처음 배포되었고, 현재 버전 6이 제공되고 있다. 이 글은 CentOS7에서 Tibero6을 설치하는 과정을 정리한 글이다.

다운로드 페이지에서 Tibero6을 Linux 64bits 용으로 다운로드 받는다. 실제 다운로드와 라이선스 발급을 위해 회원 가입이 필요하며 메일 인증을 통해 가입 처리가 이루어진다. 현재 이 글을 작성하는 시점을 기준으로 다운로드 받은 파일명은 tibero6-bin-FS07_CS_1912-linux64-174424-opt.tar.gz 이며, 이 파일을 설치하고자 하는 위치에 이동시킨 후 압축을 푼다. (필자의 경우 /etc/tibero 디렉토리로 하였고 압축을 풀면 tibero6이라는 하위 폴더가 생성되고 이 하위 폴더 안에 압축이 풀림)

tar -zxvf tibero6-bin-FS07_CS_1912-linux64-174424-opt.tar.gz

발급 받은 라이선스 파일은 설치된 디렉토리인 /etc/tibero의 하위 디렉토리인 /etc/tibero/tibero6/license에 복사한다. 참고로 라이선스 파일을 발급받기 위해서는 실치할 서버의 Host Name을 입력해야 하는데 리눅스의 경우 hostname 명령어를 입력해 쉽게 확인이 가능하다.

설치를 위한 좀 더 편리한 방법이 있을지도 모르겠으나, 티베로는 프로그램의 설치를 단순히 압축을 푸는 방식에서 시작해, 환경설정을 직접 콘솔에서 입력해 수행해 줘야 한다. 먼저 /etc/sysctl.conf의 파일에 다음의 내용을 추가한다.

kernel.shmmni = 4096
kernel.shmall = 2097152
kernel.shmmax = 2147483648
kernel.sem = 10000 32000 10000 10000

fs.file-max = 6815744

net.ipv4.ip_local_port_range = 1024 65500

/etc/security/limits.conf 파일에도 다음의 내용을 추가한다.

tibero           soft    nproc           2047
tibero           hard    nproc           16384
tibero           soft    nofile          1024
tibero           hard    nofile          65536

/etc/sysyemd/logind.conf 파일의 내용 중 RemoveIPC=no의 주석을 제거한다.

환경병수를 설정하기 위해 다음을 입력한다.

export TB_HOME=/etc/tibero/tibero6 
export TB_SID=tibero 
export LD_LIBRARY_PATH=$TB_HOME/lib:$TB_HOME/client/lib 
export PATH=$PATH:$TB_HOME/bin:$TB_HOME/client/bin

이제 티베로를 위해 이미 작성된 쉘을 실행한다.

$TB_HOME/config/gen_tip.sh

여기까지가 티베로 서버를 실해하기 위한 준비과정이며, 먼저 티베로 서버를 NOMOUNT 모드로 실행한다.

tbboot nomount

tbsql 프로그램을 통해 티베로 서버에 접속할 수 있으며, 아래처럼 sys 계정으로 초기 암호(tibero)를 지정해 접속한다.

tbsql sys/tibero

SQL> 프롬프트가 뜨면 성공한 것이고, 새로운 ‘tibero'(원한다면 다른 이름도 가능함)라는 이름의 데이터베이스를 생성한다.

create database "tibero" 
  user sys identified by tibero 
  maxinstances 8 
  maxdatafiles 100 character set MSWIN949 
  national character set UTF16 
  logfile 
    group 1 'log001.log' size 100M, 
    group 2 'log002.log' size 100M, 
    group 3 'log003.log' size 100M 
  maxloggroups 255 
  maxlogmembers 8 
  noarchivelog 
    datafile 'system001.dtf' size 100M autoextend on next 100M maxsize unlimited 
    default temporary tablespace TEMP 
      tempfile 'temp001.dtf' size 100M autoextend on next 100M maxsize unlimited 
      extent management local autoallocate 
    undo tablespace UNDO 
      datafile 'undo001.dtf' size 100M autoextend on next 100M maxsize unlimited 
      extent management local autoallocate;

데이터베이스 생성에는 다소 시간이 소요되며, 완료되면 quit를 입력해 tbsql을 종료하고, 티베로 서버를 NORMAL 모드로 실행한다.

tbboot

마지막으로 $TB_HOME/scripts의 system.sh를 실행한다. 실행과정 중 sys와 syscat의 암호를 입력해야 하는데, 각각 tibero와 syscat이다. 또한 중간 중간에 실행할 작업 수행 여부를 묻는데, 특별한 경우가 아닌한 y를 입력해 작업을 수행한다.

이제 티베로 서버가 정상적으로 수행되는지, 확인하기 위해 다음처럼 입력한다.

ps -ef | grep tbsvr

그 결과는 다음과 같다.

티베로 서버의 종료는 tbdown이며, 기본 Listener Port는 8629이다. 그리고 실제 데이터가 저장되는 데이터베이스의 위치는 설치된 티베로의 디렉토리를 기준으로 /etc/tibero/tibero6/database/{데이터베이스명}이다.

/var/log/php-fpm에 로그 파일이 존재함

[로그파일 예시]
[11-Apr-2022 12:27:11] WARNING: [pool www] seems busy (you may need to increase pm.start_servers, or pm.min/max_spare_servers), spawning 16 children, there are 3 idle, and 44 total children
[11-Apr-2022 12:27:12] WARNING: [pool www] seems busy (you may need to increase pm.start_servers, or pm.min/max_spare_servers), spawning 32 children, there are 2 idle, and 46 total children
[11-Apr-2022 12:27:15] WARNING: [pool www] server reached pm.max_children setting (50), consider raising it

/etc/php-fpm.d 디렉토리의 www.conf 파일에 pm.max_children 설정값 등이 지정되어 있음

여러 개의 속성값으로 라벨 문자열을 조립하여 실제 표시되는 라벨을 결정하는 코드의 예입니다.

CustomLabelFormatter = Xr.Class({
    name: "CustomLabelFormatter",
    extend: Xr.label.ProgrammableLabelFormatter,
    requires: [Xr.label.ILabelFormatter],
    construct: function (layer) {
        this.superclass(layer);
        this._MGN_CD = -1;
        this._MGN_DT = -1;
        this._codeValues = {
            'C01': '시설A',
            'C02': '시설B',
            'P01': '시설C',
            'P03': '시설D',
            'R03': '시설E',
            'T01': '시설F'
        };
    },
    methods: {
        value: function (shapeRow, fieldSet, attributeRow) {
            if (this._EQMT_FIXPLC_RGN_SE_CD == -1) {
                this._EQMT_FIXPLC_RGN_SE_CD = fieldSet.fieldIndex("MGN_CD");
            }

            if (this._FST_REGI_TSP == -1) {
                this._FST_REGI_TSP = fieldSet.fieldIndex("_MGN_DT");
            }

            let code = attributeRow.valueAsString(this._MGN_CD);

            // 필드 2개의 값(_MGN_CD 필드의 코드값 + _MGN_DT 의 값)을 조합한 라벨 표시, 예: 시설B(2020-07-27 14:32:32)
            return this._codeValues[code] + "(" + attributeRow.valueAsString(this._MGN_DT) + ")";
        }
    }
});

var lyr = new Xr.layers.ShapeMapLayer("lyr", ...);
let label = lyr.label();
label.enable(true);

let formatter = new CustomLabelFormatter(lyr);
label.formatter(formatter);

lm.add(lyr);

다음은 속성값으로 도형의 스타일 심벌을 지정하는 코드의 예입니다.

CustomLayerTheme = Xr.Class({
    name: "CustomLayerTheme",
    extend: Xr.theme.ProgrammableShapeDrawTheme,
    requires: [Xr.theme.IShapeDrawTheme],
    construct: function (/* ShapeMapLayer */ layer) {
        this.superclass(layer);
        this._fieldIndex = -1;
        let codes = ['R01', 'P02', 'R03', 'P01', 'P02', 'T01', 'T02', 'C01', 'C02'];
        let colors = ['#f1c40f', '#f39c12', '#e67e22', '#e74c3c', '#c0392b', '#ff0000', '#00ff00', '#0000ff', '#ff00ff'];
        let symbols = [];
        let cntCodes = codes.length;
        for (let i = 0; i < cntCodes; i++) {
            let SDS = new Xr.symbol.ShapeDrawSymbol();
            SDS.brushSymbol().color(colors[i]).opacity(0.5);
            SDS.penSymbol().color(colors[i]).width(2);

            let symbol = {
                code: codes[i],
                symbol: SDS
            };

            symbols[i] = symbol;
        }

        this._symbols = symbols;
    },
    methods: {
/* ShapeDrawSymbol */ symbol: function (/* ShapeRow */ shapeRow, /* FieldSet */ fieldSet, /* AttributeRow */ attributeRow) {
            if (this._fieldIndex === -1) {
                this._fieldIndex = fieldSet.fieldIndex("MGN_CD");
            }

            let value = attributeRow.valueAsString(this._fieldIndex);
            let symbols = this._symbols;
            let symbol = undefined;
            let cntSymbols = symbols.length;
            for (var i = 0; i < cntSymbols; i++) {
                symbol = symbols[i];
                if (value === symbol.code) {
                    break;
                }
            }
            return symbol.symbol;
        },

/* boolean */ needAttribute: function () {
            return true;
        }
    }
});


var lyr = new Xr.layers.ShapeMapLayer("lyr", ...);

var newTheme = new CustomLayerTheme(lyr)
lyr.theme(newTheme);

lm.add(lyr);

공간 분석 중, 밀도맵은 위치 데이터가 공간 상에 분포하는 경향을 매우 효과적으로 시각화할 수 있는 의사결정 지원 도구입니다. 위치 데이터의 공간 상의 위치 분포 뿐만 아니라 각 위치 데이터가 갖는 가중치값을 밀도 분석에 반영할 수 있어 위치 데이터와 통계 데이터를 조합할 수 있습니다.

밀도맵 기능의 소개를 위해 서울시의 인구 통계 데이터를 담고 있는 SHP 파일을 NexGen에 바로 불러와 밀도맵을 작성했습니다. 아래의 표는 사용한 인구 SHP 파일의 속성값에 대한 구조입니다. 통계청의 집계구 데이터를 받아 SHP 파일로 가공하였습니다.

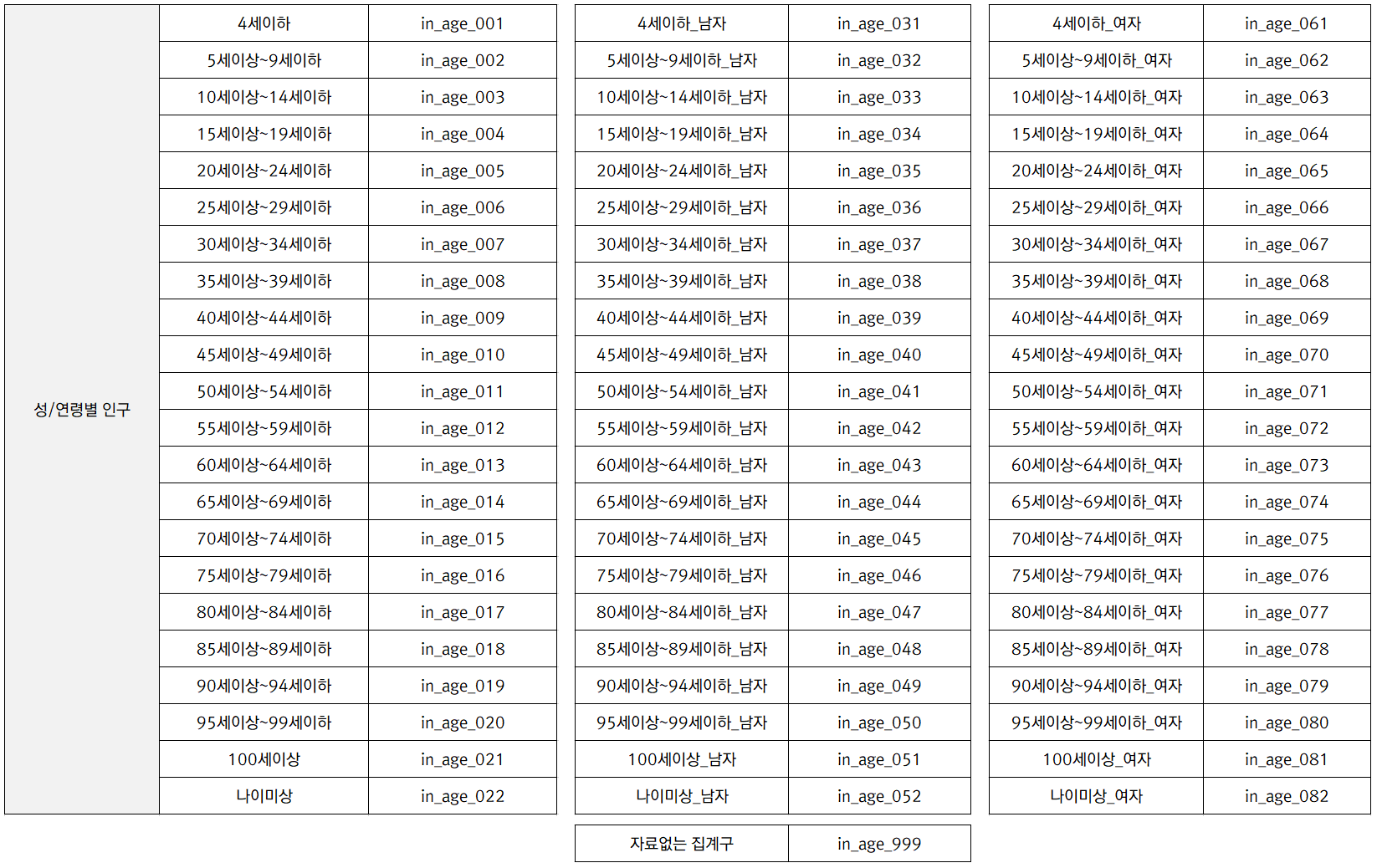
이 데이터는 아래의 URL을 통해 다운로드 받으실 수 있습니다. 통계청에서 다운로드 받은 폴리곤 타입의 SHP 파일인 집계구 데이터와 TXT 파일인 2017년도 인구 데이터를 이용해 포인트 타입의 단일 SHP 파일로 직접 가공한 것입니다. 좌표계는 EPSG:5181입니다.

아래의 시연 동영상은 위의 인구 데이터를 활용한 NexGen의 밀도맵 기능에 대한 소개입니다.

웹 기반의 GIS 솔루션인 NexGen의 밀도맵 기능은 히트맵(HeatMap) 방식이 아닌 정규분포 방식의 알고리즘을 활용하여 고품질의 밀도맵을 작성할 수 있습니다.