이 글은 http://www.lighthouse3d.com/opengl/maths/index.php?raytriint의 글을 통해 재구성한 글로, 변역하면서 쉽게 이해할 수 있도록 내용을 약간 수정했습니다.
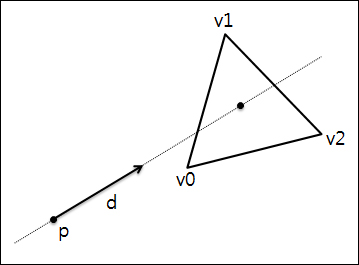
매개변수방정식의 형태로 편선(시작점에서 어떤 방향으로 무한하게 진행하는 선, Ray)과 삼각형의 폴리곤이 주어질때.. 이 둘이 교차하는가를 판단하는 방법에 대해 증명은 생략하고 그 방법에 대해서 알아 보겠습니다.
삼각형을 구성하는 점은 다음처럼 정의할 수 있습니다.
여기서, p0, p1, p2는 삼각형 위의 이미 알고 있는 점, u >= 0, v >= 0, u + v <= 1.0
그리고 편선에 대한 매개변수방정식을 다음처럼 정의할 수 있습니다.
여기서, p는 편선의 시작점으로 이미 알고 있는 점, d는 편선의 방향 벡터
이제 편선과 삼각형의 교점은 삼각형의 구성 점(u,v) = 편선의 구성 점(t) 로부터 다음과 같습니다.
결국… 교차 여부는 세 값(t, u, v)가 위의 공식을 만족하고 u와 v가 앞서 정의한 조건을 만족하면 교차하는 경우이다. 이런 수학적인 논의는 다음으로 미루기로 하고…. 여러분이 원하는 C 코드로 대신합니다.
/* a = b - c */
#define vector(a,b,c) \
(a)[0] = (b)[0] - (c)[0]; \
(a)[1] = (b)[1] - (c)[1]; \
(a)[2] = (b)[2] - (c)[2];
int rayIntersectsTriangle(float *p, float *d, float *v0, float *v1, float *v2) {
float e1[3],e2[3],h[3],s[3],q[3];
float a,f,u,v;
vector(e1,v1,v0);
vector(e2,v2,v0);
crossProduct(h,d,e2);
a = innerProduct(e1,h);
if (a > -0.00001 && a < 0.00001) return(false);
f = 1/a;
vector(s,p,v0);
u = f * (innerProduct(s,h));
if (u < 0.0 || u > 1.0) return (false);
crossProduct(q,s,e1);
v = f * innerProduct(d,q);
if (v < 0.0 || u + v > 1.0) return (false);
// at this stage we can compute t to find out where
// the intersection point is on the line
t = f * innerProduct(e2,q);
if (t > 0.00001) // ray intersection
return (true);
else // this means that there is line intersection but not ray intersection
return (false);
}
vector 함수는 두개의 좌표로부터 백터를 만드는 함수이고 innerProduct와 crossProduct는 내적과 외적을 구하는 함수입니다.