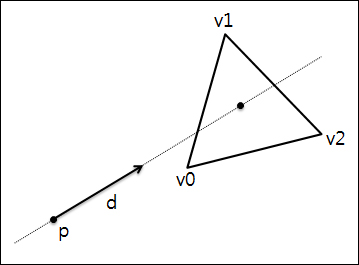
많은 스플라인의 종류 중에 하나인 큐빅 스플라인을 1차원의 보간에 적용하는 것에 대해 살펴보겠습니다. Catmull-Rom 스플라인을 구성하는 구분된 부드러운 곡선들을 나타내는 키 프레임 집합을 가지며 모든 키는 곡선 상에 위치합니다. 이 루틴을 사용하기 위해서 4개의 키 프레임 값이 필요합니다. 이 4개의 키 값을 v0, v1, v2, v3라고 하고, 여기에 보간을 위하여 v1에서 v2 사이의 지정된 0~1까지의 범위를 가지는 실수값 x가 존재합니다. 아래의 f(x)의 반환값은 x값에 의해 결정이 됩니다.
![]()
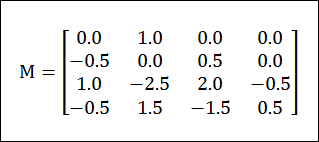
여기서 M은 다음처럼 정의됩니다.
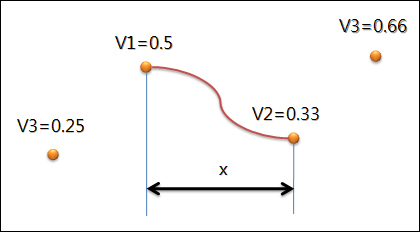
아래의 이미지는 v1에서 v2 사이의 곡선의 한 예를 나타난 것입니다. 이 곡선은 위의 수식에서 x 값을 0에서 1.0 사이의 값을 이용해 얻을 수 있습니다.
아래의 코드는 위에서 설명한 내용을 C언어로 구현한 것입니다.
/* Coefficients for Matrix M */
#define M11 0.0
#define M12 1.0
#define M13 0.0
#define M14 0.0
#define M21 -0.5
#define M22 0.0
#define M23 0.5
#define M24 0.0
#define M31 1.0
#define M32 -2.5
#define M33 2.0
#define M34 -0.5
#define M41 -0.5
#define M42 1.5
#define M43 -1.5
#define M44 0.5
double catmullRomSpline(float x, float v0,float v1, float v2,float v3) {
double c1,c2,c3,c4;
c1 = M12*v1;
c2 = M21*v0 + M23*v2;
c3 = M31*v0 + M32*v1 + M33*v2 + M34*v3;
c4 = M41*v0 + M42*v1 + M43*v2 + M44*v3;
return(((c4*x + c3)*x +c2)*x + c1);
}
이 글의 원문은 http://www.lighthouse3d.com/opengl/maths/index.php?catmullrom 입니다.