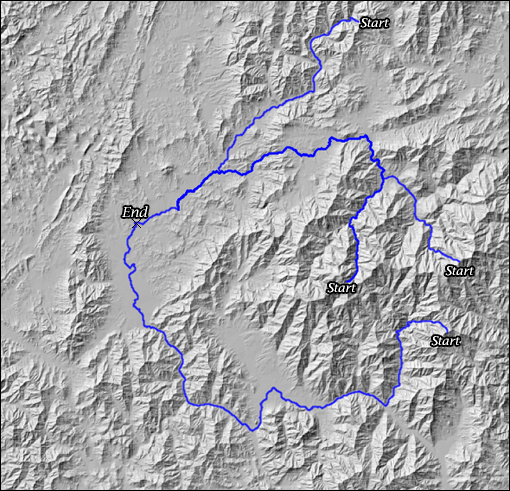
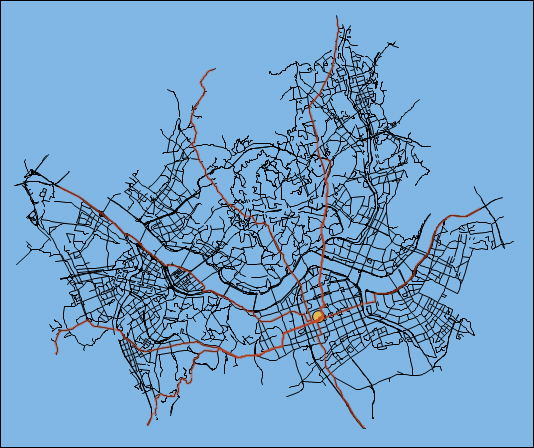
가중치 최소 비용 경로 분석을 이용하여 특정 위치에 대해 차량으로 이동할 경우 소요되는 시간에 대한 영역을 분석하는 기능에 적용해 보았습니다. 가중치는 차량이동속도로 하였습니다. 절차는 다음과 같습니다.
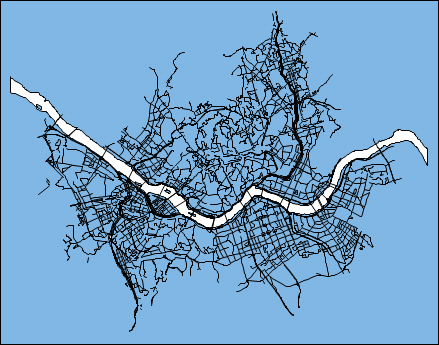
먼저 벡터 데이터로 도로망에 대한 폴리라인 데이터와 한강 수계에 대한 폴리곤 데이터를 추가합니다.
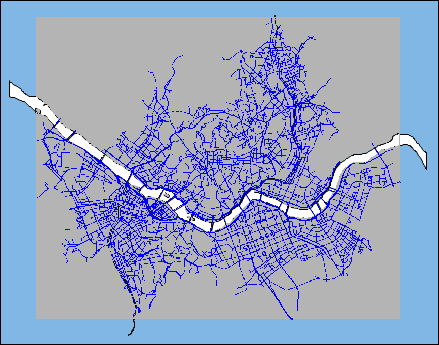
그리고, 이 두 벡터 데이터를 라스터 데이터로 변환합니다. 이때 도로망에 대한 셀값은 차량의 이동속도 값을 주는데, 여기서는 30km/h로 합니다. 그리고 수계는 차량이 들어갈 수 없으므로 NULL 값을 줍니다. 그리고 그 이외의 셀들은 도보 속도인 4km/h로 줍니다. 변환한 위의 화면을 확대해 보면 라스터로 변환된 것을 확인할 수 있습니다.
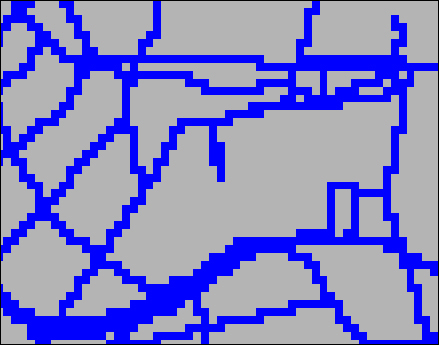
바로 파랑색이 차도이며 30의 값을 가지고, 회색은 4의 값을 가집니다.
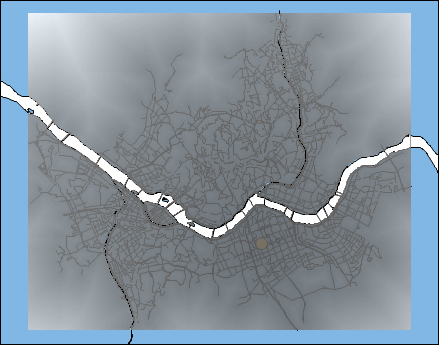
이제 목적지가 되는 포인트를 먼저 추가하고 가중치 최소 비용 경로 분석을 수행합니다. 목적지 포인트는 화면상에 노란색 원이 그에 해당하고, 가중치 최소 비용 경로 분석에 대한 결과는 위처럼 회색계열의 새로운 라스터 데이터 레이어가 생성됩니다. 분석된 셀값에는 거리에 대한 값이 반영되어 있으므로 이 거리의 값을 제거하기 위해 셀의 크기로 나누어 시간 값만 남게 합니다.
최종적으로 등고선 추출 기능(개발 맵 엔진의 확장 기능 중의 하나)를 이용하여 15분과 35분에 대한 차량이동시간을 추출한 화면이 아래와 같습니다.
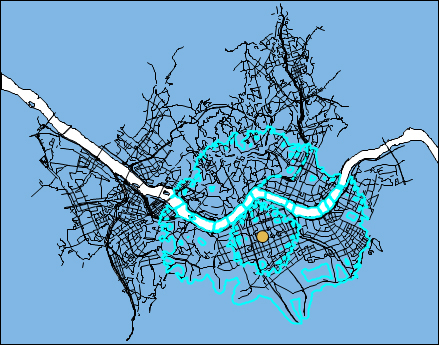
바로 위의 그림에서 추출된 영역이 목적지 포인트에 도달하는데 소요되는 최대 시간으로 각각 최대 15분이 소요되는 영역과 35분이 소요되는 영역을 나타내고 있습니다.
이 가중치 최소 비용 경로 분석은 적용하는 가중치에 따라 공간상의 이동에 대한 매우 다양한 분야에 적용할 수 있는 GIS 공간 분석 방법입니다.