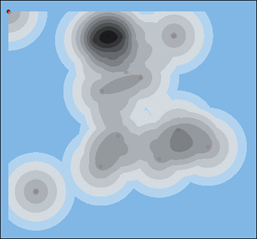
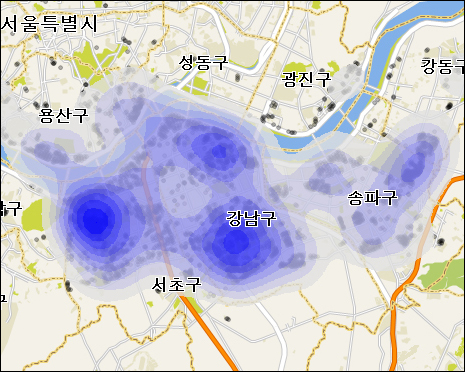
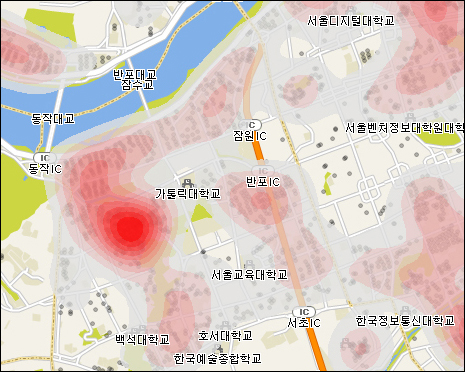
현재 작업하고 있는 지도 엔진(OpenMate XGE)에.. 각 점포가 고객을 끌어 들이는 영향권을 분석하는 기능을 개발해 보았습니다.
예를 들어서 여러개의 점포가 있다고 하면, 고객들이 어느 마트에 가서 구매를 할 것인지에 대한 분석이라고도 해석할 수가 있습니다. 또 다른 말로.. 각 점포가 고객들을 끌어 들이는 흡인력이 미치는 영향권이라고도 설명할 수 있겠고…. 이처럼 다양한 의미로 해석할 수 있는 기능이 바로 타게팅(Targeting)입니다. 이때.. 고객을 끌어들이는 다양한 인자가 존재합니다. 예를 들어서.. 유동인구, 배후인구, 교통시설, 생활수준지수 등등 매우 다양한 인자가 존재합니다.
아래의 화면은 현재 XGE 지도엔진을 이용해 만든 분석툴에서 간단히 분석해본 Targeting 화면입니다.
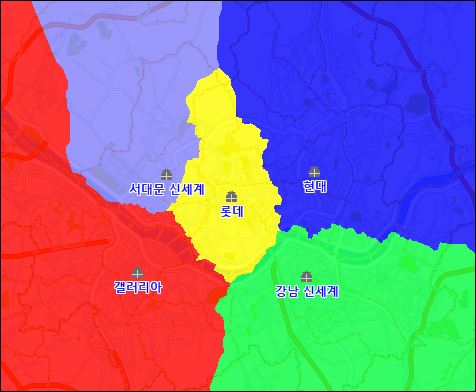
위의 결과는, 서울시에 가상으로 5개의 점포를 위치하고.. 점포가 고객을 끌어들이는 인자로써 접근성 인자만을 고려한 경우입니다. 즉, 고객이 가장 빠르게 접근할 수 있는 점포가 어디인가…. 입니다. 접근성에 대한 가중치는 도로망도를 라스터화하여 사용됩니다. 물론 도로망도는 속도라는 속성값이 있어 이 속성값을 이용해 라스터화됩니다.
이 분석 기능의 응용예는 무엇일까요? 만약 새로운 도로가 생길 경우… 기존의 점포에 미치는 영향을 분석해 본다든지…. 새로운 경쟁 점포가 생기거나 기존의 점포가 폐업했을 때… 또 어떤 영향을 미치는지 등등… 매우 다양한 분야에 응용할 수 있습니다.
근무하는 회사가 비니지스 GIS 분야이다보니.. 비니지스쪽으로 타게팅을 설명했으나… 다양한 가중치에 대한 공간 분석의 응용부분에서 이 타겟팅이 활용될 수 있습니다. 예를 들어, 토목에서, 공간상에 배수구가 다수 존재할 경우… 비가 올때 빗물이 어느 배수구로 집수 되어 빠져 나가느냐… 로 응용해 분석할수가 있습니다. 이때… 사용되는 가중치는.. 물이 흘러가는데 영향을 미치는 경사도와 표고, 그리고 땅이 물을 얼마나 흡수하느냐… 등을 생각해 볼 수 있습니다.
이상으로 짧은 지식이나마… GIS를 이용한 타겟팅에 대한 설명을 마칩니다.