원문에 대한 링크는 http://www.gisdeveloper.co.kr/attachment/1154452764.pdf 입니다. 저작권은, 원본 문서를 작성한 분의 동의를 구하지 않고 번역한지라.. 제가 없고, 원저작자에게 있습습니다. 내용상의 오류 발견하시면 거침없이 하이킥 한방.. ^^; 그럼 내용 나가십니다…
SRP : The Single Responsibility Principle
“하나의 클래스를 수정해야 한다면, 그 수정 이유는 오직 한가지여야만 한다.”
6장의 볼링 게임 시스템을 다시 상기해보면, Game 클래스는 2개의 분명한 책임을 처리해야 한다. 현재 게임 화면을 추적하는 책임과 점수를 계산하는 책임이다. 끝에서, 이 두개의 책임을 2개의 클래스로 나눠서 처리해다. Game 클래스는 게임 화면을 추적하는 책임을… Scorer 클래스는 점수를 계산하는 책임을.
음… 두개의 책임을 각각에 대한 두개의 클래스로 분리하는것이 왜 중요할까? 이유는 각 책임이 변경의 이유이기 때문이다. 시스템에 대한 변경요구가 들어오면, 클래스들에 속한 책임에서의 변경을 통해 이뤄지게 된다. 다소 좀 설명이 철학적인데… 흠.. 여하튼, 만약 어떤 클래스가 하나 이상의 책임을 가지고 있다면, 변경요구에 대한 이유 역시 하나 이상이 될 것이다.
만약, 클래스가 하나 이상의 책임을 가진다면, 그 책임들이 서로 관계를 맺게 될 것이다. 하나의 책임에 대한 변경은 다른 하나의 책임 때문에 엉키거나 변경 자체가 불가능하게 될 수 있다. 책임들에 대한 이런 관계 맺음은 변경요구 시 예상치 못한 어려운 상황을 발생시키는 설계로 치닿게 될 것이다.
예를들어보자. 그림9-1의 설계를 보면, Rectangle 클래스는 2개의 매서드를 가지고 있다. 하나는 화면에 사각형을 그리는 것. 또 하나는 넓이를 계산하는 것.
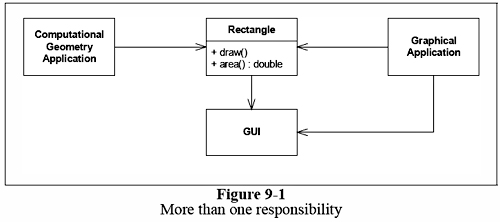
2개의 서로 다른 어플리케이션이 이 Rectangle 클래스를 사용한다. 하나의 어플리케이션은 Computational Geometry이고, Rectangle 클래스의 넓이를 얻어오기 위해 쓰일 뿐, 화면에 그리는 일은 하지 않는다. 다른 어플리케이션은 그래픽컬한 것으로 앞의 어플리케이션 처럼 클래스의 넓이도 얻어오고, 화면상에 그리기위해 Rectangle 클래스를 사용한다.
이 설계는 SRP를 위반하고 있는데, Rectangle 클래스가 2개의 책임을 갖고 있기 때문이다. 하나의 책임은 넓이 계산. 두번째 책임은 그리기. SRP 위반은 여러가지 추잡스러운 문제를 유발한다. 첫째로 반드시 Computational Geometry 어플리케이션에 쓰지도 않는 GUI 관련 모듈을 포함해야한다. 쓰지도 않는데 말이다.. 찝찝해… 두번째는, 하나의 어플리케이션에서 Rectangle를 어떤 이유때문에 변경했을때, 또 다른 어플리케이션에 영향을 미친다는 것이다. 이런.. 이런..
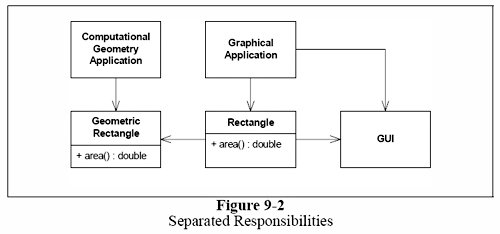
더 나은 설계는 그럼 9-2처럼, 두개의 완전히 독립된 클래스에 각각 하나씩의 책임을 분리하는 것이다. 이 설계는 Rectangle의 클래스의 넓이 계산 책임은 GeometricRectangle 클래스를 만들어 넣는다. 이대로라면, 사각형을 표시하는 기능이 Compution Geometry 어플리케이션에 영향을 미치지 않는다.
책임이라는게 무엇인가?
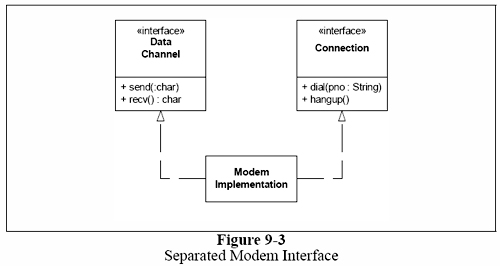
SRP 즉, 단일책임원리에서, ‘변경의 이유’로써 ‘책임’을 정의했다. 클래스를 변경해야할 하나 이상의 이유를 생각할 수 있다면, 그 클래스는 하나 이상의 책임을 갖고 있다는 의미이다. 우리는 책임을 그룹 단위로 생각하려는 경향이 있다. 예를들자면, 리스트 9-1에서와 같이, Modem 인터페이스를 살펴보자. 대부분의 사람들에게는 Modem 인터페이스는 완벽하게 보인다. 즉, 4개의 함수는 분명히 Modem의 기능이 틀림없다.

그러나, 여기에는 2개의 책임이 존재한다. 첫번째 책임은 연결관리이고, 두번째 책임은 데이터 통신이다. dial과 hangup 함수는 모뎀의 연결을 관리하고, send와 recv는 데이터 통신 함수이다.
이 2개의 책임을 분리해야하는가? 대부분의 경우, 확실하게 그래야만 한다. 이 2개의 함수셋(dial과 hanup 함수셋, send와 recv 함수셋)은 “공통점”을 가지고 있지 않다. 이 2개의 함수셋의 변경 이유는 서로 다르다.
더욱이, 이들을 사용하는 어플리케이션의 부분 역시 완전히 다르다. 마찬가지로 이러한 다른 부분들은 서로 다른 이유로 변경될 것이다.
그래서, 그림9-3이 더 나은 설계이다. 2개의 분리된 인터페이스에 2개의 책임을 나눴다. 최소한 이 방법은, 2개의 책임이 서로 결합함으로써, 변경에 방해가 되는 것으로부터 어플리케이션을 보호해줄 것이다.
그러나……. 결국에는 ModemImplementation 클래스에서 두 책임이 재결합하고 있다는 점이다. 이것은 바람직하지 않은 것이지만, 어쩔 수 없는 경우일지도 모른다. 그러나, 이들의 인터페이스를 분리함으로써, 이 두 책임을 분리시켜야 한다.
ModelImplementation는 못쓸 클래스처럼 보일지도 모른다. 그러나, 모든 의존성들이 이 클래스로인해 제거 된다는 점. 어느 무엇도 이 클래스에 의존할 필요가 없다는 것이다. 어느 무엇도 main을 제외하고 이것의 존재를 알 필요가 없다는 점이다. 그러니까.. 쉽게 말하면 Modem 관련 기능을 위해 우리가 알아야할 클래스는 ModemImplementation이 아니고 앞서 2개의 인터페이스 DataChannel, Connection 이다. 이것이 ISP가 아닌가….
ModemImplementation는 단지 OS나 하드웨어에 따라 달리 구현되는 구현부일 뿐이다. 인터페이스와 구현의 분리가 완벽하게 이뤄지고 있다는 것이다. 그래서, 우리는 우리는 울타리 뒤에 흉직한 것들을 놓는 것이다. 즉, 울타리는 앞서 2개의 인터페이스이고 흉직한 것들은 ModemImplementation이다. 흉직하다라는 표현을 한 이유는 변경사항이 발생할때마다 변경해야할 곳이기에 개발자의 수고가 가장 많기 때문이다. 이것으로 인해, 어플리케이션의 나머지 부분 역시 오염되는 것을 최소화 할 수 있다.
결론
SRP는 가장 간단한 객체지향 원리 중에 하나이면서 옳바르게 사용하기가 가장 어려운 것중에 하나이다. 책임의 결합은 우리가 은연중에 하게 되는 습관인듯하다. 이러한 책임을 찾아 분리하는 것이 소프트웨어 설계의 아주 많은 부분이다. 사실, SRP 이외의 다른 객체지향원리도 SRP의 원리가 적용된다.