#include "stdafx.h"
#include
#include
int _tmain(int argc, _TCHAR* argv[])
{
int a = 1;
#pragma omp parallel
{
#pragma omp sections firstprivate(a) lastprivate(a)
{
#pragma omp section
{
Sleep(1000);
printf("section 1: a 초기값 = %d\n", a);
a = 2;
printf("section 1: a 수정값 = %d\n", a);
}
#pragma omp section
{
printf("section 2: a 초기값 = %d\n", a);
a = 3;
printf("section 2: a 수정값 = %d\n", a);
}
}
}
printf("a 최종값 = %d\n", a);
return 0;
}
이 코드는 스레드를 2개 사용하고 있습니다. 즉 section 지시어를 통해 13~18번 코드를 실행하는 스레드 하나와 20~24번 코드를 실행하는 스레드 하나입니다. 10번 코드에서 lastprivate(a)라는 보조 지시어를 통해 2개의 스레드에서 연산한 결과 a가 복사됩니다. 14번 코드에 Sleep 함수를 호출함으로써 두개의 스레드 중 a에 2를 할당한 스레드가 가장 마지막에 끝나도록 했습니다. a에 2를 할당한 스레드가 마지막에 종료되니.. 이 2개의 스레드가 끝나면 a 값은 항상 2가 될거라 예상됩니다.
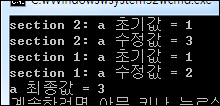
근데.. 보는 바와 같이 a의 최종값이 3이라고 합니다.. ㅡOㅡ;; 실행 흐름을 봐도 가장 먼저 a 수정값으로 3을 할당하고 다음 실행으로 a 수정값으로 2를 할당하는 순서입니다. 실행 순서는 예상과 같은데.. 결과는 반대입니다.. ㅡOㅡ;; 아직 OpenMP를 학습하는 단계인지라.. 이해가 떨어져서 그런 것인지.. 아니면 OpenMP의 BUG인지… 모를 일입니다.. 누구 아시는 분 코칭 부탁드립니다.