k-Means 알고리즘을 이용한 군집화(Cluster)

다음과 같은 데이터가 존재한다고 합시다.

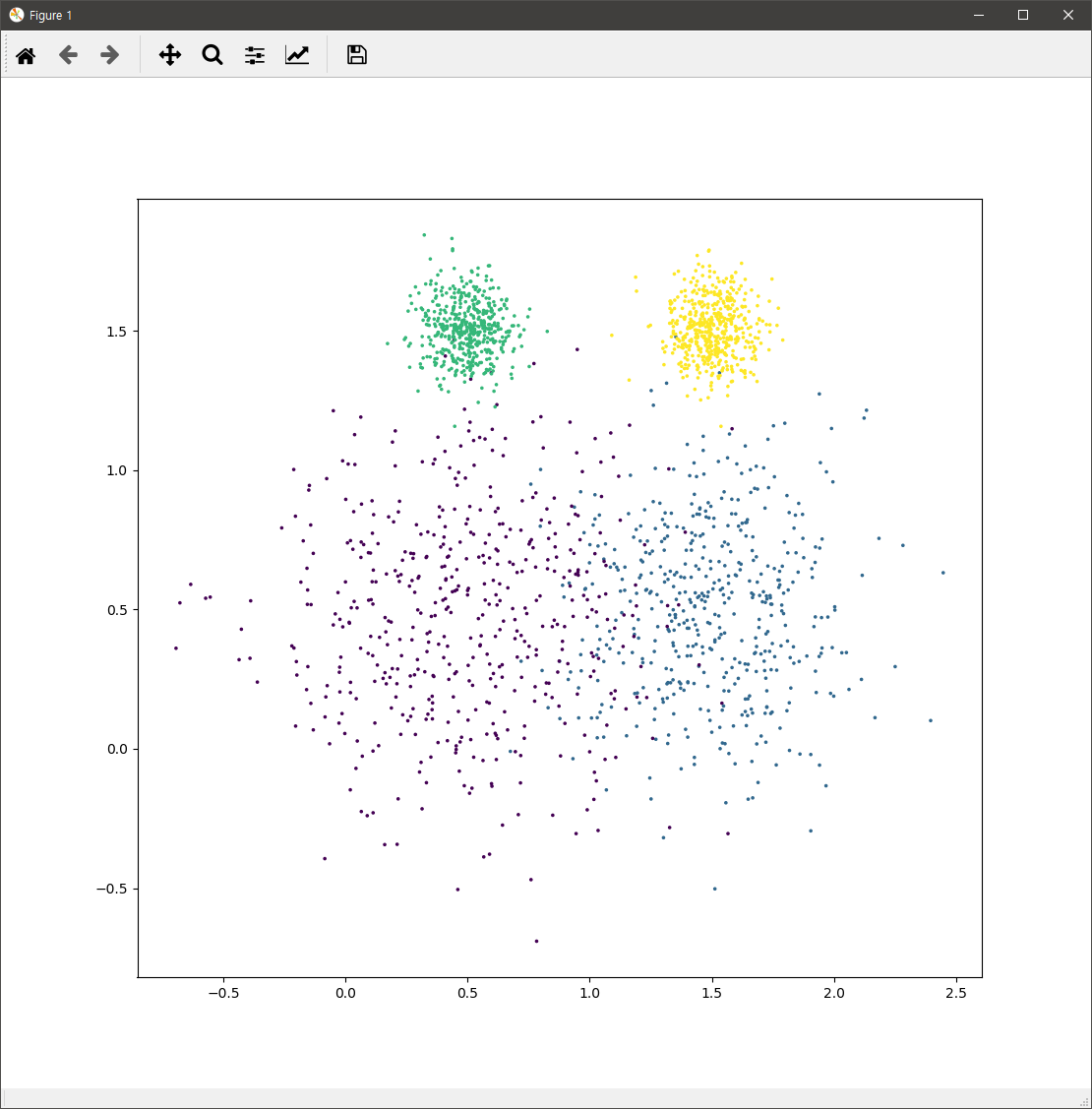
위의 데이터는 아래의 코드로 생성된 것입니다.

import sklearn
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

blob_centers = np.array(
    [[ 0.5,  0.5 ],
     [ 1.5,  0.5 ],
     [ 0.5,  1.5],
     [ 1.5,  1.5]])
blob_std = np.array([0.4, 0.3, 0.1, 0.1])

X, y = make_blobs(n_samples=2000, centers=blob_centers, cluster_std=blob_std, random_state=3224)

def plot_data(X, y):
    plt.scatter(X[:, 0], X[:, 1], c=y, marker='.', s=10)

plot_data(X, y)
plt.show()

위의 데이터는 4개로 구룹지을 수 있다는 것을 코드를 통해 알 수 있습니다. 이제 이 데이터를 k-Means를 이용하여 4개로 군집화하는 코드는 살펴보면 다음과 같습니다.

k = 4
kmeans = KMeans(n_clusters=k)
y_pred = kmeans.fit_predict(X)

위의 코드를 통해 kmeans 모델은 새로운 샘플 데이터에 대해서 4개의 그룹중 어떤 그룹에 포함되는지 예측할 수 있습니다. 이에 대한 시각화 코드는 다음과 같습니다.

def plot_decision_boundaries(clusterer, X, y, resolution=500):
    mins = X.min(axis=0) - 0.1
    maxs = X.max(axis=0) + 0.1
    xx, yy = np.meshgrid(np.linspace(mins[0], maxs[0], resolution), np.linspace(mins[1], maxs[1], resolution))
    Z = clusterer.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)

    plt.contourf(Z, extent=(mins[0], maxs[0], mins[1], maxs[1]), cmap="gist_stern")
    plt.contour(Z, extent=(mins[0], maxs[0], mins[1], maxs[1]), linewidths=1, colors='k')
    plot_data(X, y)

plot_decision_boundaries(kmeans, X, y)
plt.show()

위 코드의 결과는 다음과 같습니다.

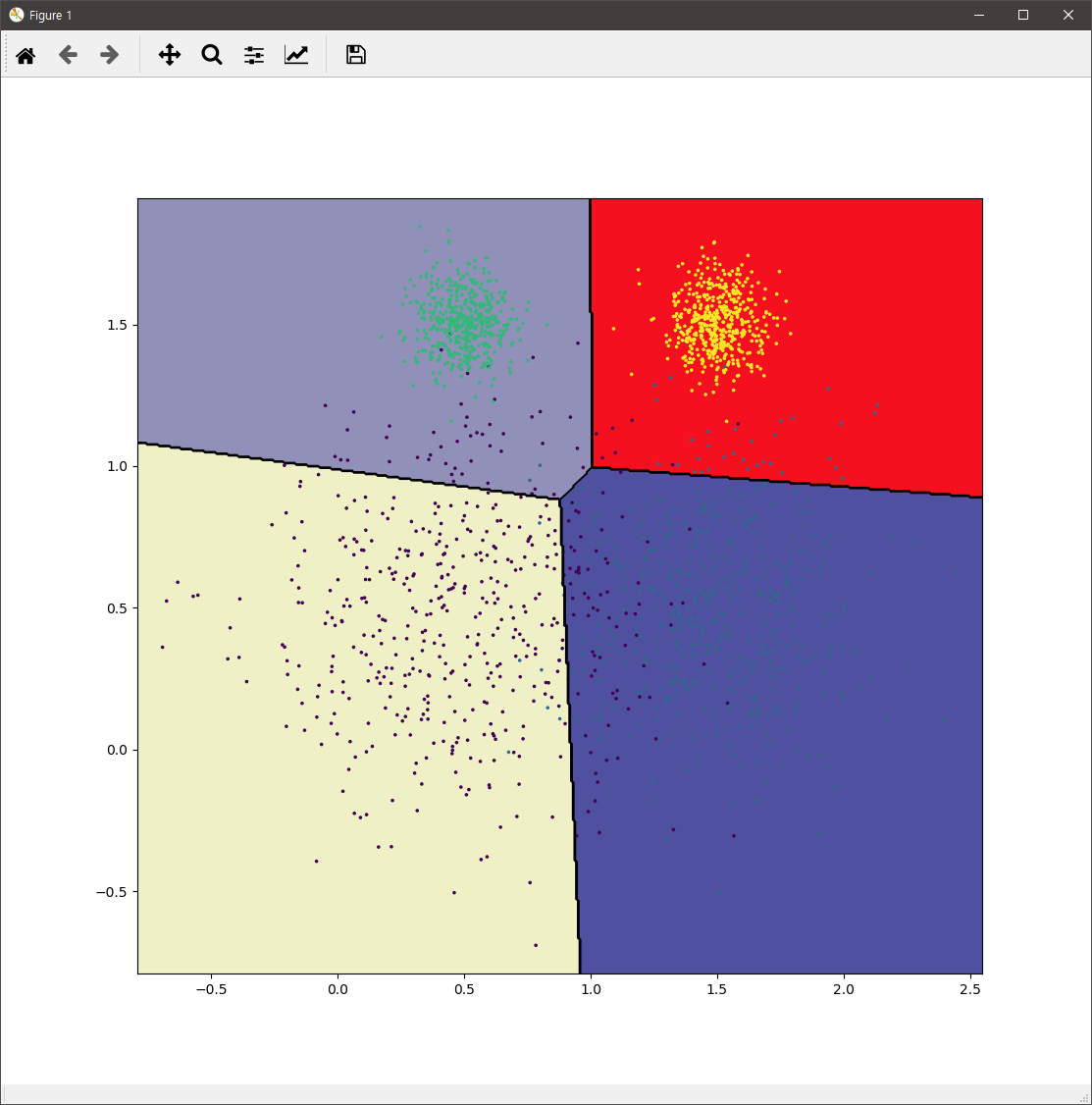
실제 k-means를 적용할 시에는 군집화할 개수를 알 수 없는 경우가 대부분입니다. 위의 코드에서는 k 값인데요. 이 값을 효과적으로 결정하기 위해서는 실루엣 다이어그램(Silhouette Diagram)을 통해 효과적으로 파악할 수 있습니다.