이 글의 원문은 https://opencv-python-tutroals.readthedocs.io/en/latest/py_tutorials/py_ml/py_knn/py_knn_understanding/py_knn_understanding.html#knn-understanding 입니다.
kNN은 감독학습(Supervised Learning)을 통한 가장 단순한 분류 알고리즘 중에 하나입니다. 알고리즘에 대한 아이디어의 시작점은 공간 상의 시험 데이터와 가장 가까운 것들을 묶는다는 것입니다. 아래의 이미지를 통해 볼 수 있죠.
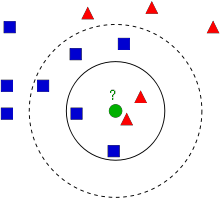
위의 이미지에는 파란색 사각형과 빨간색 삼각형으로 구성되어 있습니다. 즉 2개의 그룹이 존재합니다. 각 그룹을 클래스(Class)라고 부릅니다. 이제 새로운 요소(초록색 원)이 나타났습니다. 이 새로운 요소는 파란색 사각형으로 분류될까요, 아니면 빨간색 삼각형으로 분류 될까요? 이를 kNN 알고리즘을 활용해 보자는 것입니다.
한가지 방법은 이 초록색 원과 가장 가까운 이웃을 찾는 것입니다. 위의 그림에서는 빨간색 삼각형과 가장 가깝다는 것을 확인할 수 있습니다. 그래서 이 초록색 원은 빨간색 삼각형으로 분류됩니다. 이 방법은 오직 가장 가까운 이웃에 의한 분류이므로 단순히 ‘가장 가까운 이웃(Nearest Neighbour)’ 이라고 부릅니다.
그러나 여기에는 문제가 있습니다. 빨간색 삼각형이 가장 가까울 수 있습니다. 그러나 이 초록색 원 주위에는 아주 많은 파란색 사각형이 존재한다면 어떨까요? 그러면 파란색 사각형은 빨간색 삼각형보다 더 많은 영향력을 초록색 원에 주고 있다고 할 수 있습니다. 그래서 가장 가까운 것만으로는 충분하지 않습니다. 대신 어떤 k-Nearest 군이라는 개념을 검사해야 합니다. 그림에서, 3 Nearest 군, 즉 k=3이라고 합시다. 초록색 원과 가장 가까운 3(k값)개를 취합니다.그러면 2개의 빨간색과 1개이 파란색이 있고 초록색은 하나 더 많은 빨간색으로 분류됩니다. k=7이라면? 5개이 파란색과 2개의 빨간색이 존재하고 파란색으로 분류됩니다. k값을 변경하는 것이 전부입니다. 재미있는 것은 만약 k=4일때입니다. 이 경우 2개의 빨간색과 2개의 파란색이 존재합니다. 애매해지죠. 그래서 k값은 홀수로 잡는 것이 좋습니다. 이러한 분류 방법을 k-Nearest Neighbor이라고 합니다.
지금까지 언급한 kNN에서는 k개의 이웃 모두를 동일하게 다루고 있습니다. 이게 맞는 것일까요? 예를 들어, k=4인 경우에 분류가 애매해 진다고 했습니다. 그러나 좀더 살펴보면, 2개의 빨간색은 다른 2개의 파란색보다 좀더 가깝습니다. 그렇다면 빨간색에 더 많은 가중치를 줘야 합니다. 이를 수학적으로 어떻게 설명할까요? 가까운 요소들에 대해 그 거리에 따라 계산된 가중치를 줘야 합니다. 가까운 요소에는 더 높은 가중치를, 상대적으로 멀리 있는 요소에는 낮은 가중치를 말이죠. 결국 가장 높은 가중치의 합을 가지는 쪽으로 분류될 수 있는데, 이를 Modified kNN이라고 합니다.
여기에 몇가지 중요한 것을 발견할 수 있습니다.
- 공간 상에 분포되는 빨간색과 파란색 요소 전체에 대한 정보가 필요합니다. 왜냐하면 새로운 요소와 이미 존재하는 각 요소 사이의 거리를 구해야 하기 때문입니다. 그래서 매우 많은 요소가 존재할 경우 더 많은 메모리와 더 많은 계산 시간이 필요할 것입니다.
- kNN에는 어떤 형태의 훈련과 준비가 필요치 않습니다.
OpneCV에서 kNN을 살펴봅시다.
이 글에서는 먼저 앞서 살펴본 그림처럼 2개의 군으로 구성된 단순한 예를 활용하겠습니다. 다음 글에서 좀더 복잡한 예를 처리할 것이구요.
빨간색 군은 Class-0(0이라 표기)이라고 하고, 파란색 군은 Class-1(1이라고 표기)이라고 합시다. 25개의 요소를 새성하고 각 요소에 대해 Class-0과 Class-1 중 하나로 정합니다. 이를 위해 Numpy에서 난수 생성자가 유용합니다.
시각화는 Matplotlib가 유용합니다. 빨간색 군은 빨간색 삼각형으로, 파란색 군은 파란색 사각형으로 표시합니다.
import cv2 import numpy as np import matplotlib.pyplot as plt # Feature set containing (x,y) values of 25 known/training data trainData = np.random.randint(0,100,(25,2)).astype(np.float32) # Labels each one either Red or Blue with numbers 0 and 1 responses = np.random.randint(0,2,(25,1)).astype(np.float32) # Take Red families and plot them red = trainData[responses.ravel()==0] plt.scatter(red[:,0],red[:,1],80,'r','^') # Take Blue families and plot them blue = trainData[responses.ravel()==1] plt.scatter(blue[:,0],blue[:,1],80,'b','s') plt.show()
실행 결과는 다음과 같습니다. 난수를 사용했으므로 실행 결과는 매번 다릅니다.
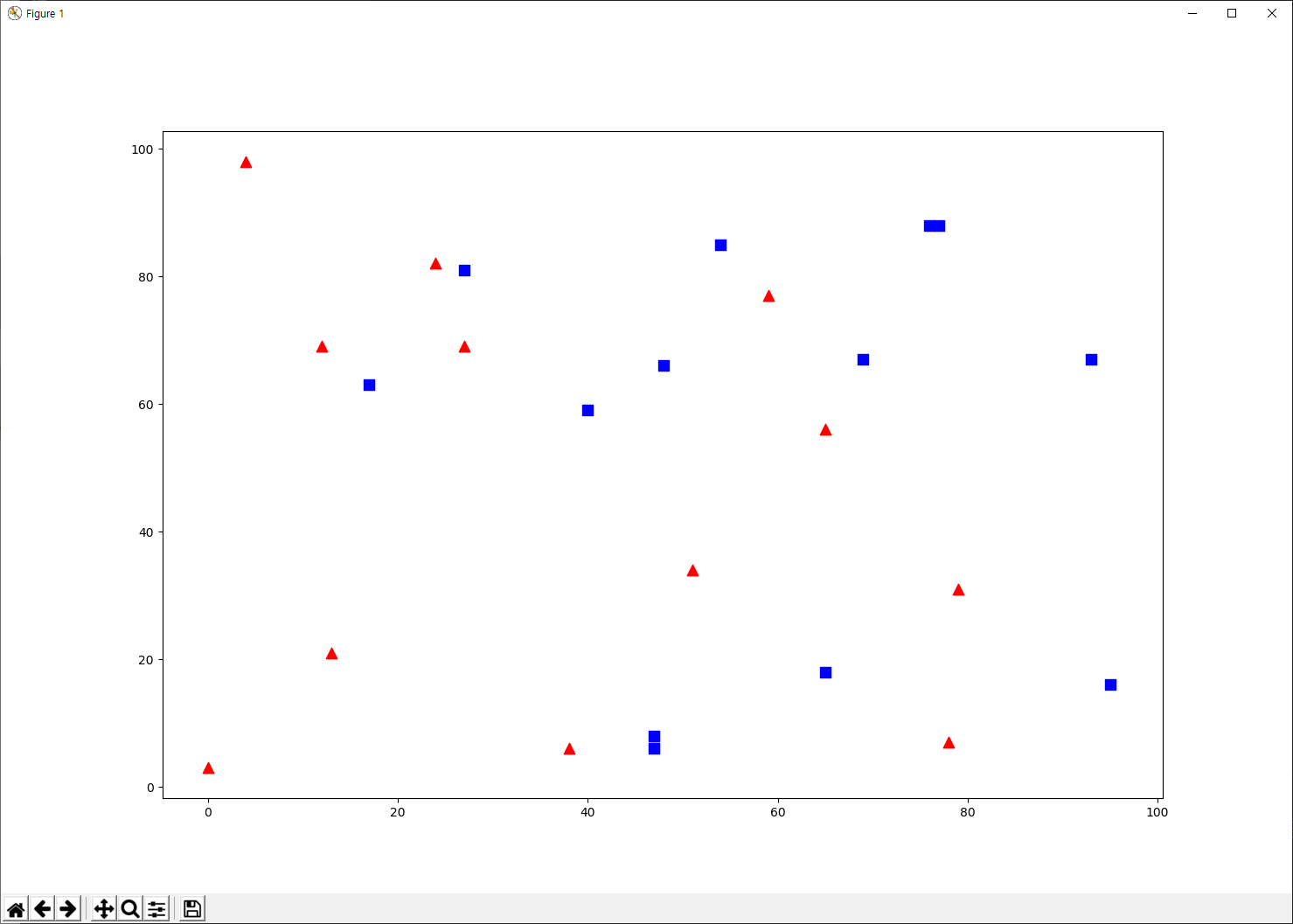
다음으로 trainData와 responses 변수를 전달하여 kNN 알고리즘을 초기화 합니다(검색 트리가 구성됩니다).
이제 새로운 요소를 가져와 이 새로운 요소가 빨간색 또는 파란색 중 어디로 분류될지 OpenCV의 kNN을 이용합니다. kNN으로 가기 전에 먼저 새로운 요소, 즉 테스트 데이터에 대한 정보를 알아야 합니다. 이 테스트 데이터는 실수형 타입의 배열로써 크기는 
입니다. 이제 새로운 요소와 가장 가까운 요소를 찾습니다. 가장 가까운 요소를 몇개까지 찾을 것인지 지정할 수 있습니다. 이러한 검색의 결과는 다음과 같습니다.
- kNN 이론의 기반하여 새로운 요소에 Class-0과 Class-1과 같은 이름이 반환됩니다. 만약 매우 단순한 Nearest Neighbour 알고리즘을 원한다면 k=1로 지정합니다.
- 새로운 요소와 각각의 가까운 요소 사이의 거리값이 반환됩니다.
지금까지의 설명에 대한 코드는 다음과 같습니다. 이 추가 코드는 앞의 코드 중 18번째 줄에 추가됩니다.
newcomer = np.random.randint(0,100,(1,2)).astype(np.float32)
plt.scatter(newcomer[:,0],newcomer[:,1],80,'g','o')
knn = cv2.ml.KNearest_create()
knn.train(trainData, cv2.ml.ROW_SAMPLE, responses)
ret, results, neighbours ,dist = knn.findNearest(newcomer, 3)
print("result: ", results)
print("neighbours: ", neighbours)
print("distance: ", dist)
실행 결과는 다음과 같습니다.
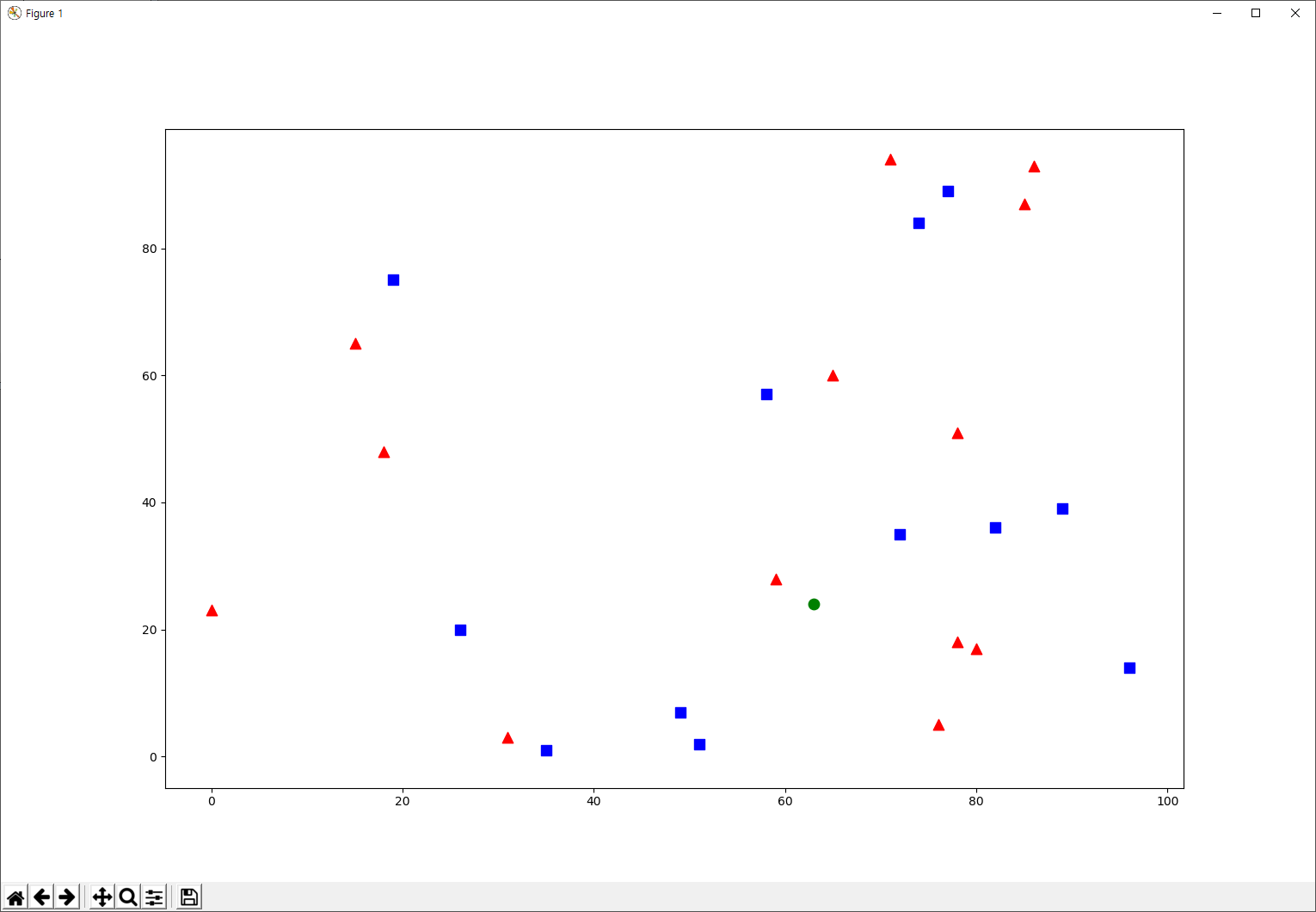
콘솔에 출력된 결과는 다음과 같구요.
result: [[0.]]
neighbours: [[0. 1. 0.]]
distance: [[ 32. 202. 261.]]
결과는 빨간색(Class-0)으로 분류되었다는 것과 새로운 요소(초록색 원)에서 가장 가까운 3개의 요소가 있으며, 검색된 3개의 요소는 빨간색 요소(Class-0)이 2개이고 파란색 요소(Class-1)이 1개이며 각각의 거리 값입니다.
만약 새로운 요소의 개수가 많다면 배열로 전달할 수 있으며, 각각의 분류 결과는 배열로써 얻어집니다. 아래는 10개의 새로운 요소에 대한 분류에 대해 앞의 코드를 대체하는 코드입니다.
newcomers = np.random.randint(0,100,(10,2)).astype(np.float32)
plt.scatter(newcomers[:,0],newcomers[:,1],80,'g','o')
knn = cv2.ml.KNearest_create()
knn.train(trainData, cv2.ml.ROW_SAMPLE, responses)
ret, results, neighbours ,dist = knn.findNearest(newcomers, 3)
print("result: ", results)
print("neighbours: ", neighbours)
print("distance: ", dist)