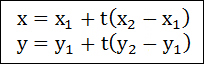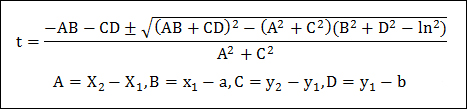WPF에서 트랙볼(Trackball) 구현하기
http://blogs.msdn.com/danlehen
개요
보통 3D 모델을 화면에 표시하면, 그 다음으로 할 작업은 마우스로 모델을 회전해 보는 것이다. 마우스를 통해 3D 오브젝트를 회전하기 위한 가장 일반적인 기술은 트랙볼 기능이라고 알려져 있다. 이 글은 트랙볼이란 무엇이며, 이를 구현하기 위한 방 법을 살펴본다. 이 글의 마지막에 언급한 링크는 WPF 어플리케이션에서 마우스를 이용하여 카메라를 회전할 수 있는 샘플 코드이다.
그림1a) 기본 구성을 가지는 호랑이 모델
1. 소개
트랙볼은 마우스의 이동을 3D 회전으로 변환한 것이다. 이는 마우스의 위치를 그림2에서 보여지는 것처럼 Viewport3D 전면에 존재하는 가상의 구면으로 마우스의 위치를 투영한 것이다. 마우스를 움직임으로써 카메라(또는 장면)은 마우스 포인터 아래의 구면 위의 동일한 위치를 유지하면서 회전된다.
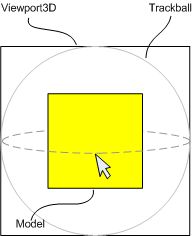
그럼2a) 정육면체 모델을 가지고 있는 Viewport3D와 사용자 시점에서 본 트랙볼
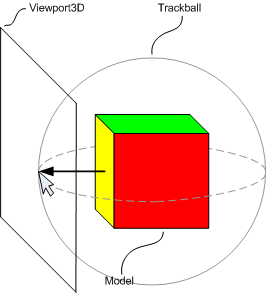
마우스가 수평으로 이동될 때, Y 축에 대한 회전은 마우스 포인터 아래에 동일한 위치가 유지되어야한다.
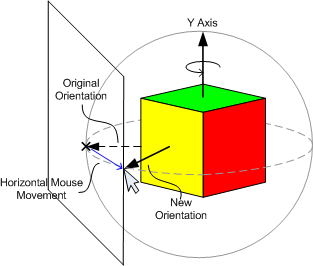
그림3) 수평으로 마우스를 움직이는 것은 Y축에 대해 장면을 회전시킨다.
이와 유사하게 마우스 위치를 수직으로 변경시키는 것은 X 축에 대한 회전을 발생시킨다.
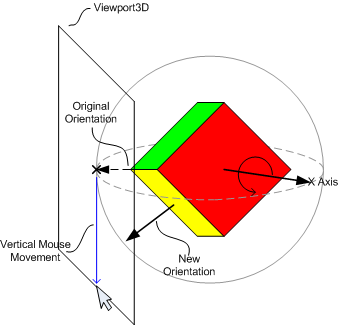
이러한 인터페이스는 X와 Y축에 대한 회전의 조합을 적용하여 사용자가 원하는 방향에서 모델을 살펴볼 수 있는 매우 직관적인 방법이다.
2. 회전 계산
각각 마우스 이동 이벤트에서 마우스 포인터 아래의 동일한 위치를 유지하는 회전을 계산할 필요가 있으며 이를 수행하기 위한 2가지 단계가 필요하다. 첫번째는 마우스 포인터가 구면의 어느 위치에 있는지 계산하는 것이다. 두번째는 예전 위치를 새로운 위치로 변환하기 위해 필요한 회전을 계산하는 것이다.
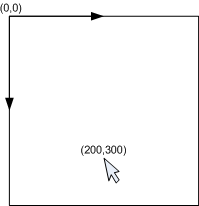 그림5a) 마우스 위치는 좌상단에 (0,0)을 가지는 UIElement의 좌표공간 상에서 알 수 있다.
그림5a) 마우스 위치는 좌상단에 (0,0)을 가지는 UIElement의 좌표공간 상에서 알 수 있다.
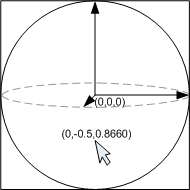
그림5b) 2차원 마우스 위치를 Viewport3D의 구면 상의 위치로 투영하며 이 위치는 3차원이다.
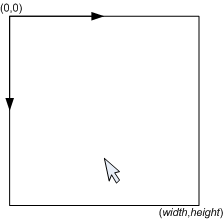
그림6a) UIElement의 좌표계
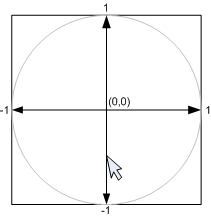
그림6b) 우리가 정한 트랙볼의 좌표계
이를 수행하기 위해 Viewport3D의 경계를 [0,0]-[2,2] 범위로 맵핑되도록 크기 변환을 한다. 다음으로 좌상단 코너에서 중심 위치를 원점으로 움직이도록 변환한다. 위치를 범위 [-1,1]-[1,-1]로 놓는다. 마지막으로 2D 좌표계에서 Y축이 위 방향 대신 아래방향으로 향하도록 한다.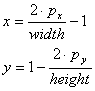
// 범위가 0,0] -[2,2]가 되도록 크기 변환 double x = p.x / (width / 2); double y = p.y / (height / 2); // 0,0을 중심으로 이동 x = x - 1; // Y축이 아래 방향 대신 위방향이 되도록 반전 y = 1 - y;
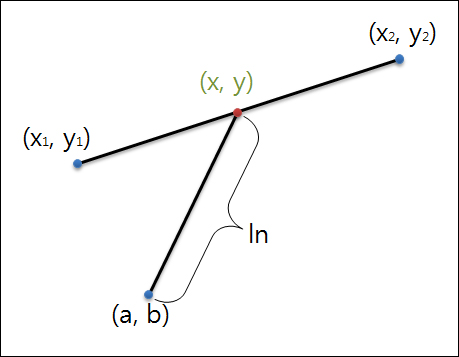
이제 z값을 가진 x와 y 위치에 대한 구면 상의 위치를 알수 있게 되었다. 구의 반지름이 1이므로 z는 다음의 공식으로 구할 수 있다.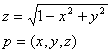
double z2 = 1 - x*x - y*y; double z = z2 > 0 ? Math.Sqrt(z2) : 0; Vector3D p = new Vector3D(x, y, z); p.Normalize();
이제 마우스 포인터 아래의 구면 상의 위치 (x, y, z)를 알게 되었다.
2.2 포인트 간의 회전
우리는 마우스 이동시에 마우스 포인트 아래에 대한 구면 상의 동일한 위치를 유지하는 모델의 회전을 원한다. 마지막으로 호출된 마우스 이동 이벤트에서 구면상의 이전 위치를 기억하고 마우스 포인터 아래의 현재 위치로 변환될 회전을 만들어 이를 수행할 수 있다.
이 회전을 계산하기 위해 2가지가 필요하다.
- 회전 축
- 회전 각도
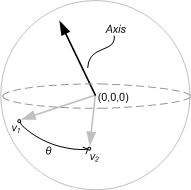
구가 원점을 중심으로 하고 있으므로 위치를 백터로 해석할 수 있다. 회전 축과 회전 각도는 각각 백터의 내적과 외적을 사용하여 쉽게 구할 수 있다:
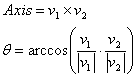
Vector3D axis = Vector3D.CrossProduct(v1, v2); double theta = Vector3D.AngleBetween(v1, v2);
일단 축과 회전 각도 모두를 알게 되었다면 남은 것은 새로운 회전을 현재 방향에 적용하는 것이다:
// 각도에 음수를 취하는데, 이는 카메라를 회전하기 때문이다. // 장면을 대신 회전한다면 이렇게 해서는 않된다. Quaternion delta = new Quaternion(axis, -angle); // RotateTransform3D로부터 현재의 방향을 얻는다. RotateTransform3D rt = (RotateTransform3D)camera.Transform; AxisAngleRotation r = (AxisAngleRotation3D)rt.Rotation; Quaternion q = new Quaternion(r.Axis, r.Angle); // 이전 방향과 delta를 합성한다. q *= delta; // 새로운 방향을 Rotation3D에 다시 지정한다. r.Axis = q.Axis; r.Angle = q.Angle;
3. 기타 세부사항
2절에서 간과한 몇가지 세부사항이 있다. 첫번째는 Viewport3D가 정사각형이라는 가정하고 구면 상에 마우스 포인터의 투영을 계산했다는 것이다. 만약 Viewport3D가 정사각형이 아니라면 트랙볼은 실제로 타원체의 모습일 것이다.
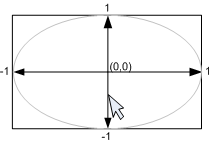
이러한 효과는 실제로 주목할 만한 사실은 아니지만 정사각형이 아닌 사각형의 너비와 높이에 대한 비율이 크다면 짧은 축을 따라 더 빠르게 회전하는 현상이 발생한다. 이러한 현상을 막고자 한다면 2D 포인트를 (width, height) 구 대신에 가로와 세로의 길이가 동일한 구로 맵핑하면 된다. 한가지 좋은 예는 가로와 세로 길이를 모두 min(width, height)이다.
또 다른 이슈는 트랙볼 상의 위치에 맵핑되지 않는 마우스 포인터가 발생할 경우에 대한 처리이다.
한가지 해결법은 이런 경우에 z를 0으로 한정하는 것으로 2.1절의 끝에서 보였다:
double z = z2 > 0 ? Math.Sqrt(z2):0;
기술적으로 x와 y를 정규화해야 하는데, 이는 Z=0인 평면에서 트랙볼 상에 가장 가까운 위치를 찾기 위함이다. 정규화하지 않는다면 반환된 위치는 구면상에 있지 않게 된다:
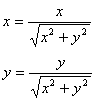
그러나, 2.2절에서 우리는 정규화된 벡터에 해당하는 Vector3D.AngleBetween(v1, v2)를 사용했다. 이는 위에서 처럼 정규화된 x와 y와 동일한 결과이다.
우리는 또한 모델과 카메라의 초기 위치에 대해 이야기 하지 않았다. 이 구현은 모델이 원점에 존재하며 카메라는 원점을 보고 있고 모델이 보이는 위치에 놓여졌다고 가정한다.
마지막으로 이 글은 확대/축소에 대해 언급하지 않았지만 샘플 코드에서 이에 대한 구현을 포함하고 있으므로 살펴보기 바란다.
4. 샘플 코드
샘플 코드는 재사용이 가능한 3개 파일로 구성된다.
Trackball.cs : 유틸리티 클래스 파일이며 FrameworkElement에 대한 마우스 이벤트를 처리한다. 또한 결과로써 회전과 크기변환을 가지는 Transform3D를 업데이트 한다.
Trackport.proj : loose.xaml 로부터 Model3D을 읽고 표시하는 UserControl이며 트랙볼 기능(Trackball.cs)이 적용되었다.
ModelViewer.proj : 그림 1의 모델 뷰어 어플리케이션(Trackport.proj를 사용하는 예)
감사의 말
모델 뷰 샘플을 제공해준 나의 아내, Bonnie에게 감사한다.