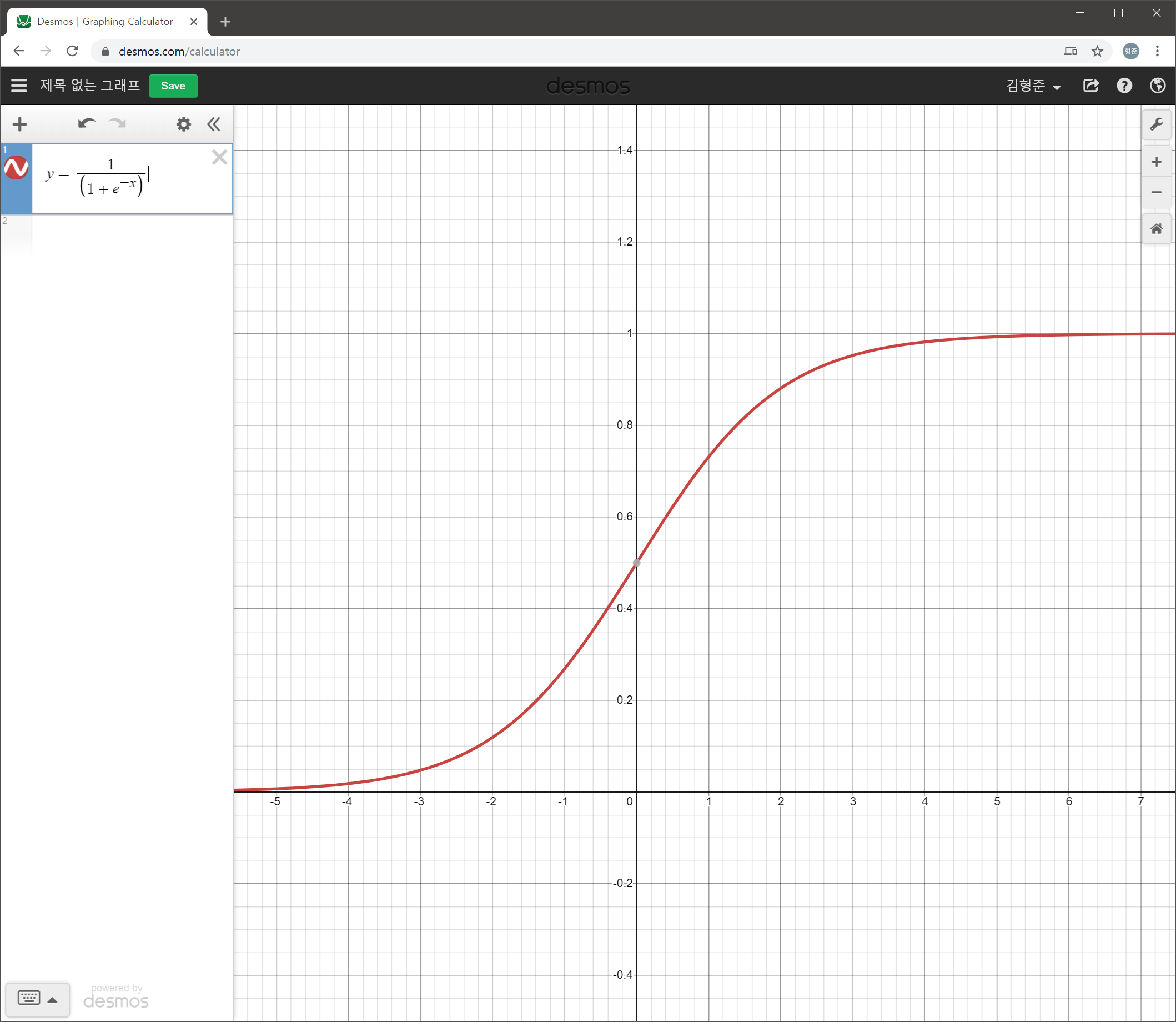
SVM(Support Vector Machine)은 데이터 분석 중 분류에 이용되며 지도학습 방식의 모델입니다. SVM에 대한 좋은 구현체는 사이킷-런(scikit-learn)인데, 이를 이용해 SVM에 대한 내용을 정리해 봅니다.
먼저 학습을 위한 입력 데이터가 필요한데, scikit-learn은 데이터 분류를 목적으로 데이터를 생성해 주는 make_blobs라는 함수를 제공합니다. 이를 이용해 아래처럼 2종류의 총 40개의 샘플 데이터를 생성합니다.
import numpy as np import matplotlib.pyplot as plt from sklearn import svm from sklearn.datasets.samples_generator import make_blobs X, y = make_blobs(n_samples=40, centers=2, random_state=20)
위에서 생성한 데이터 샘플을 SVM으로 학습시키는 코드는 다음과 같습니다.
clf = svm.SVC(kernel='linear') clf.fit(X, y)
SVM은 선형 분류와 비선형 분류를 지원하는데, 그 중 선형 모델을 위해 kernel을 linear로 지정하였습니다. 비선형에 대한 kernel로는 rbf와 poly 등이 있습니다.
학습된 SVM 모델을 통해 데이터 (3,4)를 분류하는 코드는 다음과 같습니다.
newData = [[3,4]] print(clf.predict(newData))
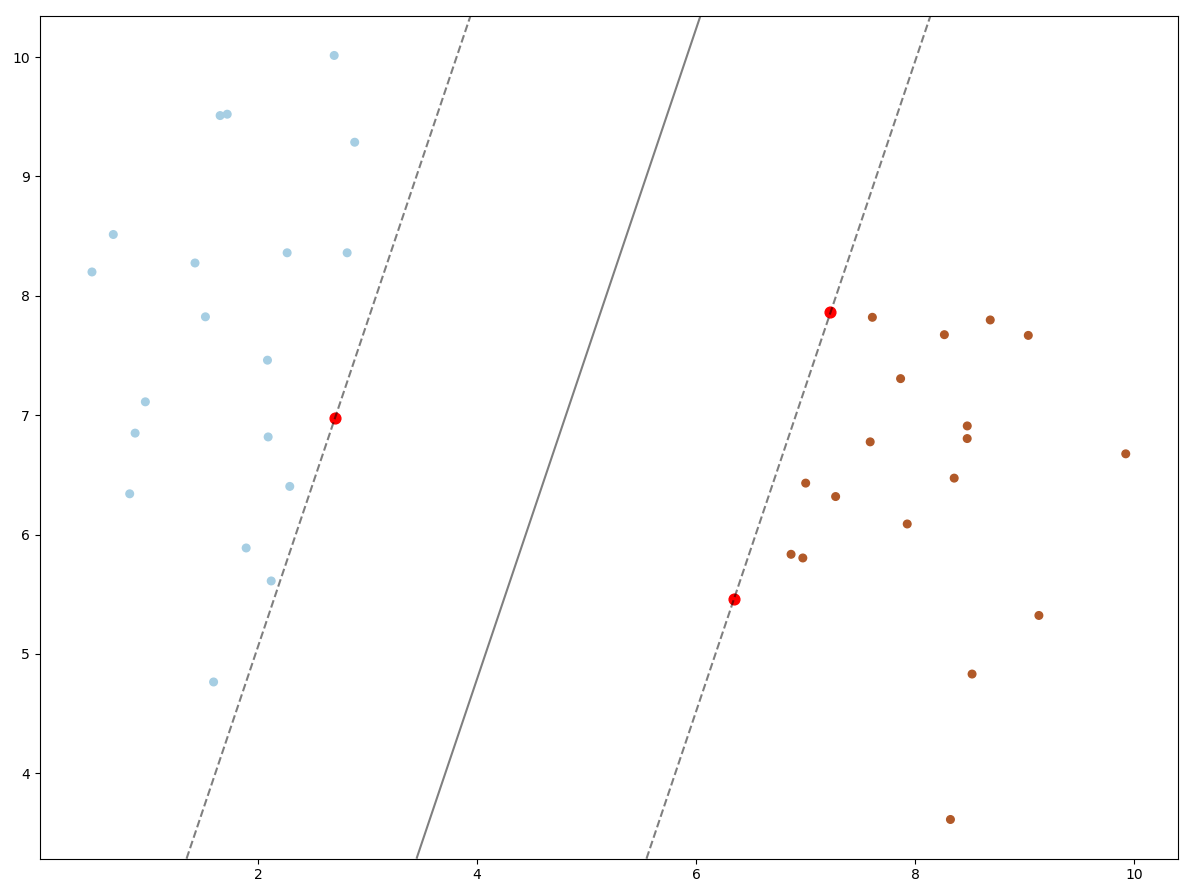
다음은 시각화입니다. 샘플 데이터와 초평면(Hyper-Plane), 지지벡터(Support Vector)를 그래프에 표시하는 코드는 다음과 같습니다.
# 샘플 데이터 표현 plt.scatter(X[:,0], X[:,1], c=y, s=30, cmap=plt.cm.Paired) # 초평면(Hyper-Plane) 표현 ax = plt.gca() xlim = ax.get_xlim() ylim = ax.get_ylim() xx = np.linspace(xlim[0], xlim[1], 30) yy = np.linspace(ylim[0], ylim[1], 30) YY, XX = np.meshgrid(yy, xx) xy = np.vstack([XX.ravel(), YY.ravel()]).T Z = clf.decision_function(xy).reshape(XX.shape) ax.contour(XX, YY, Z, colors='k', levels=[-1,0,1], alpha=0.5, linestyles=['--', '-', '--']) # 지지벡터(Support Vector) 표현 ax.scatter(clf.support_vectors_[:,0], clf.support_vectors_[:,1], s=60, facecolors='r') plt.show()
결과는 다음과 같습니다. 빨간색 포인트가 지지벡터이고, 진한 회색선이 초명편입니다.
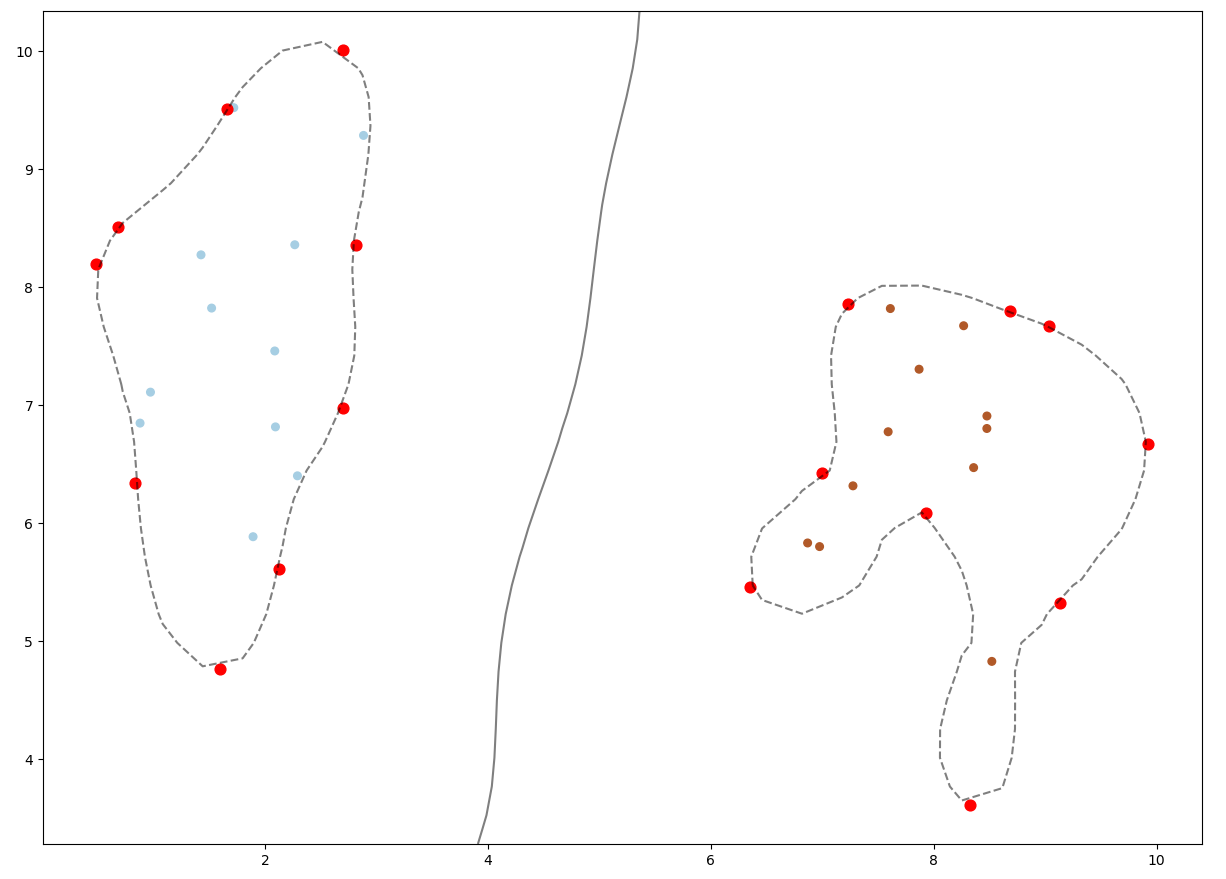
다음은 비선형 SVM로써 kernel이 rbf인 결과 그래프입니다.