GIS 기반의 AI 기술 중, 항공영상이나 위성영상 지도로부터 특정 대상을 추출해 내는 기능이 있습니다. 특정 대상이라함은 영상 지도에서 ‘건물’이나 ‘차량’, ‘비닐하우스’ 등과 같은 것을 말합니다. AI에서는 이처럼 특정 대상을 분류하고 검출하는 모델을 딥러닝(Deep Learning)을 통해 신경망 차원에서 학습 및 개발할 수 있는데요. 이처럼 이미지를 통해 특정 대상을 검출하는 방식으로는 Detection과 Segmentation 방식이 있습니다. 이 두가지에 대한 보다 자세한 내용은 아래의 글을 참고 하시기 바랍니다.
위의 글은 Detection과 Segmentation에 대한 개념적 소개와 그 차이점, 그리고 실제로 웹에서 이미지를 입력하면 해당 이미지에서 ‘사람’을 추출해 내는 실제 개발된 시스템에 대한 소개입니다.
이미지에 대한 Detection과 Segmentation에 대한 신경망 모델은 매우 다양합니다. 모델에 따라 분류 정확도 및 정밀도에 대한 지표에 차이가 있습니다. 이런 점에서 신경망 모델의 선택도 중요하지만, 이보다 훨씬 더 중요한 것은 신경망 학습에 사용되는 데이터, 즉 학습 데이터가 얼마나 정확하고 얼마나 더 많은가가 더욱 중요합니다.
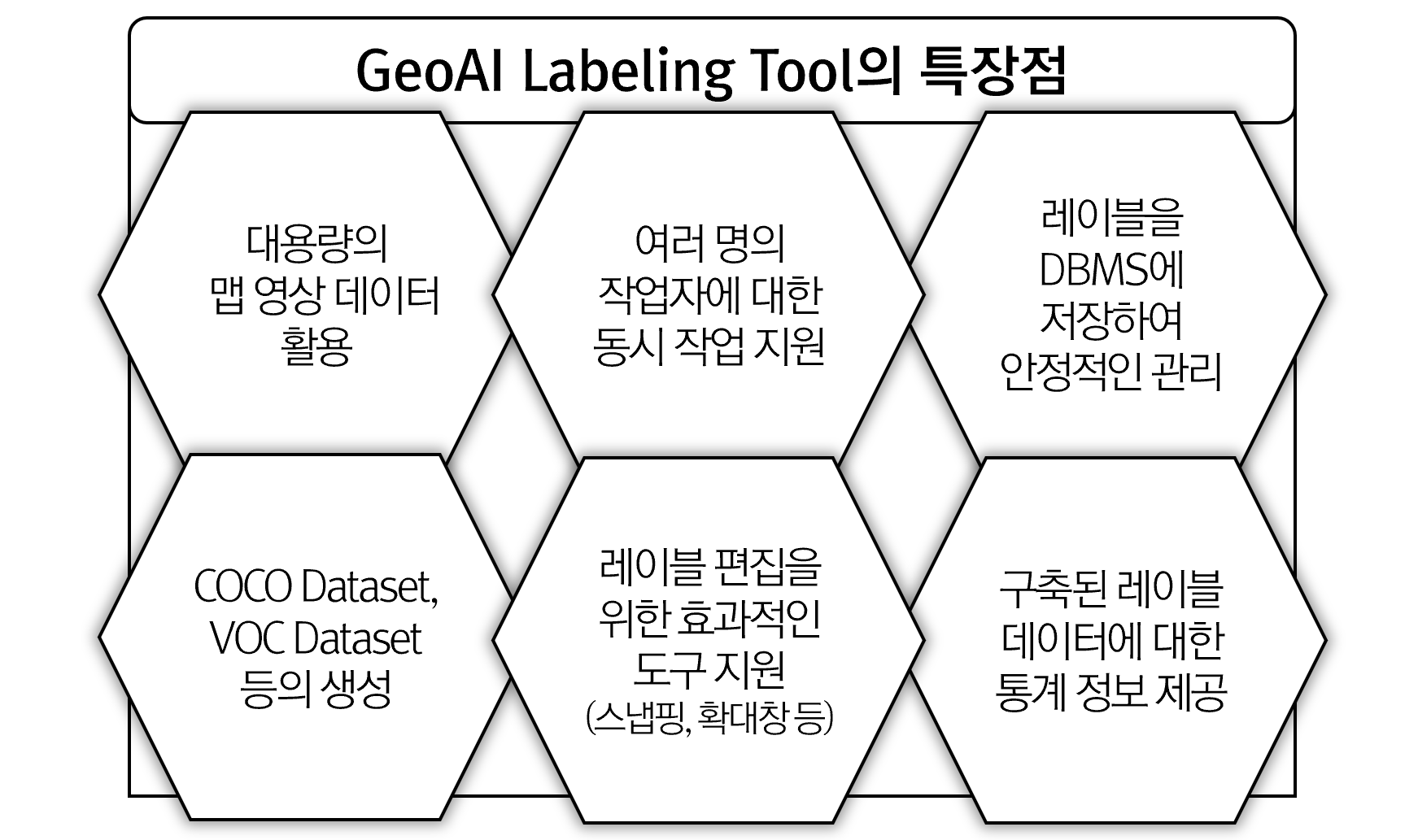
이 글에서 소개하는 GeoAI 레이블링 툴은 항공영상이나 위성영상에 대해 Detection과 Segmentation을 위한 데이터를 빠르게 구축할 수 있는 툴로써 다음과 같은 장점을 갖습니다.
아래의 동영상은 GeoAI Labeling Tool에서 Detection 데이터를 구축하는 내용을 담고 있습니다.
추가로 아래의 동영상은 GeoAI Labeling Tool에서 Segmentation 데이터를 구축하는 내용을 담고 있습니다.

