GLSL 예제 : Texture(MultiTexture) – 3/3
원문 : http://www.lighthouse3d.com/opengl/glsl/index.php?textureMulti
멀티 텍스쳐링은 GLSL에서는 정말 쉽다. 해야할 것은 두개의 텍스쳐에 접근하는 일이 전부다. 그리고 이 장에서는 동일한 텍스쳐 좌표를 사용할 것이기 때문에 버텍스 쉐이더를 재작성하지 않고 이전 강좌의 것을 그대로 사용한다. 프레그먼트 쉐이더 또한 두개의 텍스쳐 색상을 추가하는 최소한의 변화만 있다.
varying vec3 lightDir,normal;
uniform sampler2D tex,l3d;
void main()
{
vec3 ct,cf;
vec4 texel;
float intensity,at,af;
intensity = max(dot(lightDir,normalize(normal)),0.0);
cf = intensity * (gl_FrontMaterial.diffuse).rgb +
gl_FrontMaterial.ambient.rgb;
af = gl_FrontMaterial.diffuse.a;
texel = texture2D(tex,gl_TexCoord[0].st)+
texture2D(l3d,gl_TexCoord[0].st);
ct = texel.rgb;
at = texel.a;
gl_FragColor = vec4(ct * cf, at * af);
}
 그리고 이제, 약간 다른 특별한 것을 해보자: Glow in the Drak Effect. 이 특별한 효과는 두번째 텍스쳐를 어둠속에서 타오르는듯하게 보이는 것이다. 예를들어, 완전이 밝아졌다가 어두워지는 듯한 효과.
그리고 이제, 약간 다른 특별한 것을 해보자: Glow in the Drak Effect. 이 특별한 효과는 두번째 텍스쳐를 어둠속에서 타오르는듯하게 보이는 것이다. 예를들어, 완전이 밝아졌다가 어두워지는 듯한 효과.
 두 단계로 최종 색상을 다시 계산해야 하는데, 먼저 첫번째 텍스쳐를 프레그먼트 색상으로 조정된 상태의 색상을 계산하고, 이후에 두번째 텍스쳐 유닛을 강도에 기반해서 추가하는 것이다.
두 단계로 최종 색상을 다시 계산해야 하는데, 먼저 첫번째 텍스쳐를 프레그먼트 색상으로 조정된 상태의 색상을 계산하고, 이후에 두번째 텍스쳐 유닛을 강도에 기반해서 추가하는 것이다.
intensity가 0이라면, 두번째 텍스쳐가 전체적으로 완전하게 표시된다. 반대로 intensity가 1이라면, 두번째 텍스쳐를 10% 정도만 표시되도록 한다. 이런 표시를 위해 smoothStep라는 함수를 통해 구현할 것이다. 이 함수의 시그니쳐는 다음과 같다.
genType smoothStep(genType edge0, genType edge1, genType x);
만약 x<=edge0이면 결과는 0이고, x>=edge1이면 1 그리고 edge0< x <edge1이면 Hermit 보간 연산이 수행된다. 우리의 경우 다음 함수를 호출한다.
coef = smoothStep(1.0, 0.2, intensity);
다음은 프레그먼트 쉐이더 코드이다.
varying vec3 lightDir,normal;
uniform sampler2D tex,l3d;
void main()
{
vec3 ct,cf,c;
vec4 texel;
float intensity,at,af,a;
intensity = max(dot(lightDir,normalize(normal)),0.0);
cf = intensity * (gl_FrontMaterial.diffuse).rgb +
gl_FrontMaterial.ambient.rgb;
af = gl_FrontMaterial.diffuse.a;
texel = texture2D(tex,gl_TexCoord[0].st);
ct = texel.rgb;
at = texel.a;
c = cf * ct;
a = af * at;
float coef = smoothstep(1.0,0.2,intensity);
c += coef * vec3(texture2D(l3d,gl_TexCoord[0].st));
gl_FragColor = vec4(c, a);
}
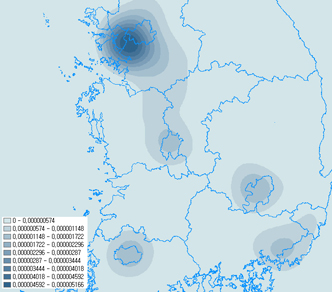
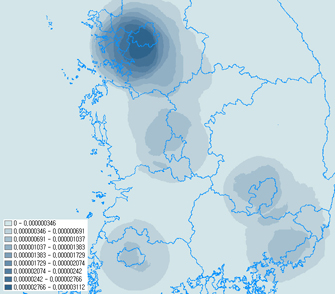 밀도 개산의 가장 많은 활용처는 포인트나 폴리라인에 대해 어느 부분에 밀집되어져 있느냐를 시각적으로 효과적으로 파악할 수 있다는 점입니다. 또한 이러한 밀도 개산에 의해 생성된 Grid 데이터를 여러개를 동시에 중첩하여 여러개의 인자들에 대한 복합적인 분석에 매우 효과적으로 활용됩니다. XGE에서는 ArcGIS의 밀도 분석은 물론이고 시각적으로 어느 부분이 가장 밀집도가 높으냐라는 판단이 아니라, 정확히 이 부분이 가장 밀집도가 높다라는 “제시”까지 제공할 예정입니다. “제시”는 기본이 되는 밀도개산 기능이 잘 완료가 되면 쉽게 구현할것으로 판단됩니다.
밀도 개산의 가장 많은 활용처는 포인트나 폴리라인에 대해 어느 부분에 밀집되어져 있느냐를 시각적으로 효과적으로 파악할 수 있다는 점입니다. 또한 이러한 밀도 개산에 의해 생성된 Grid 데이터를 여러개를 동시에 중첩하여 여러개의 인자들에 대한 복합적인 분석에 매우 효과적으로 활용됩니다. XGE에서는 ArcGIS의 밀도 분석은 물론이고 시각적으로 어느 부분이 가장 밀집도가 높으냐라는 판단이 아니라, 정확히 이 부분이 가장 밀집도가 높다라는 “제시”까지 제공할 예정입니다. “제시”는 기본이 되는 밀도개산 기능이 잘 완료가 되면 쉽게 구현할것으로 판단됩니다. 
 마이크로소프트(MS)사의 창업자 빌 게이츠는 중학교 2학년 때부터 컴퓨터 프로그래밍으로 돈을 벌었다. 지난 2000년 서울의 한 소년도 같은 나이에 이미 회원 수 400명이 넘는 하이텔 소프트웨어 프로그래머 동호회를 책임지고 있었다.
마이크로소프트(MS)사의 창업자 빌 게이츠는 중학교 2학년 때부터 컴퓨터 프로그래밍으로 돈을 벌었다. 지난 2000년 서울의 한 소년도 같은 나이에 이미 회원 수 400명이 넘는 하이텔 소프트웨어 프로그래머 동호회를 책임지고 있었다. 






 그리고 이제, 약간 다른 특별한 것을 해보자: Glow in the Drak Effect. 이 특별한 효과는 두번째 텍스쳐를 어둠속에서 타오르는듯하게 보이는 것이다. 예를들어, 완전이 밝아졌다가 어두워지는 듯한 효과.
그리고 이제, 약간 다른 특별한 것을 해보자: Glow in the Drak Effect. 이 특별한 효과는 두번째 텍스쳐를 어둠속에서 타오르는듯하게 보이는 것이다. 예를들어, 완전이 밝아졌다가 어두워지는 듯한 효과. 두 단계로 최종 색상을 다시 계산해야 하는데, 먼저 첫번째 텍스쳐를 프레그먼트 색상으로 조정된 상태의 색상을 계산하고, 이후에 두번째 텍스쳐 유닛을 강도에 기반해서 추가하는 것이다.
두 단계로 최종 색상을 다시 계산해야 하는데, 먼저 첫번째 텍스쳐를 프레그먼트 색상으로 조정된 상태의 색상을 계산하고, 이후에 두번째 텍스쳐 유닛을 강도에 기반해서 추가하는 것이다.