머신러닝으로 풀고자 하는 문제에 대한 입력값, 즉 특성은 그 상황에 따라 몇개에서 수백, 수천만개 이상으로 이루어질 수 있습니다. 그렇다고 이 모든 특성이 문제 해결을 위해 중요한 것은 아닙니다. 어떤 특성은 문제 해결에 미치는 영향이 미미하거나 아예 없는 경우도 있습니다. 이럴때 문제 해결에 미미한 영향을 가지는 특성은 제거하는 것은 해당 문제를 풀 수 있는 가능성을 높여준다는 점에서 매우 의미가 큽니다. 문제 해결의 가능성을 높여지는 것 뿐만이 아니라 불필요한 특성을 줄여줌으로써 학습 속도가 향상되며, 더 적은 학습 데이터만으로도 높은 정확도의 결과를 얻을 수 있습니다. 또한 특성을 2개 또는 3개로 줄임으로써 우리에게 익숙한 2차원과 3차원의 공간에 데이터를 시각화하여 어떤 통찰을 얻을 수도 있습니다.
이 글은 특성수를 줄이는, 즉 차원을 축소하는 방법에 몇가지를 언급합니다. 구체적인 예로 다음과 같은 3개의 특성으로 구성된 3차원의 데이터를 특성 2개인 2차원의 데이터로 축소함에 있어서, 최대한 원래 데이터가 가지고 있는 좋은 특성을 유지하도록 하는데, 이는 통계학적으로는 분석을 최대한 보존하는 방향이기도 합니다. 먼저 특성을 줄일 대상이 되는 원본 데이터를 구성하고 이를 3차원으로 시각화하는 코드는 다음과 같습니다.
from sklearn.datasets import make_swiss_roll
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
X, t = make_swiss_roll(n_samples=500, noise=0.1, random_state=3224)
fig = plt.figure(figsize=(6, 5))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=t, cmap=plt.cm.hot)
plt.show()
위 코드의 결과는 다음과 같습니다.
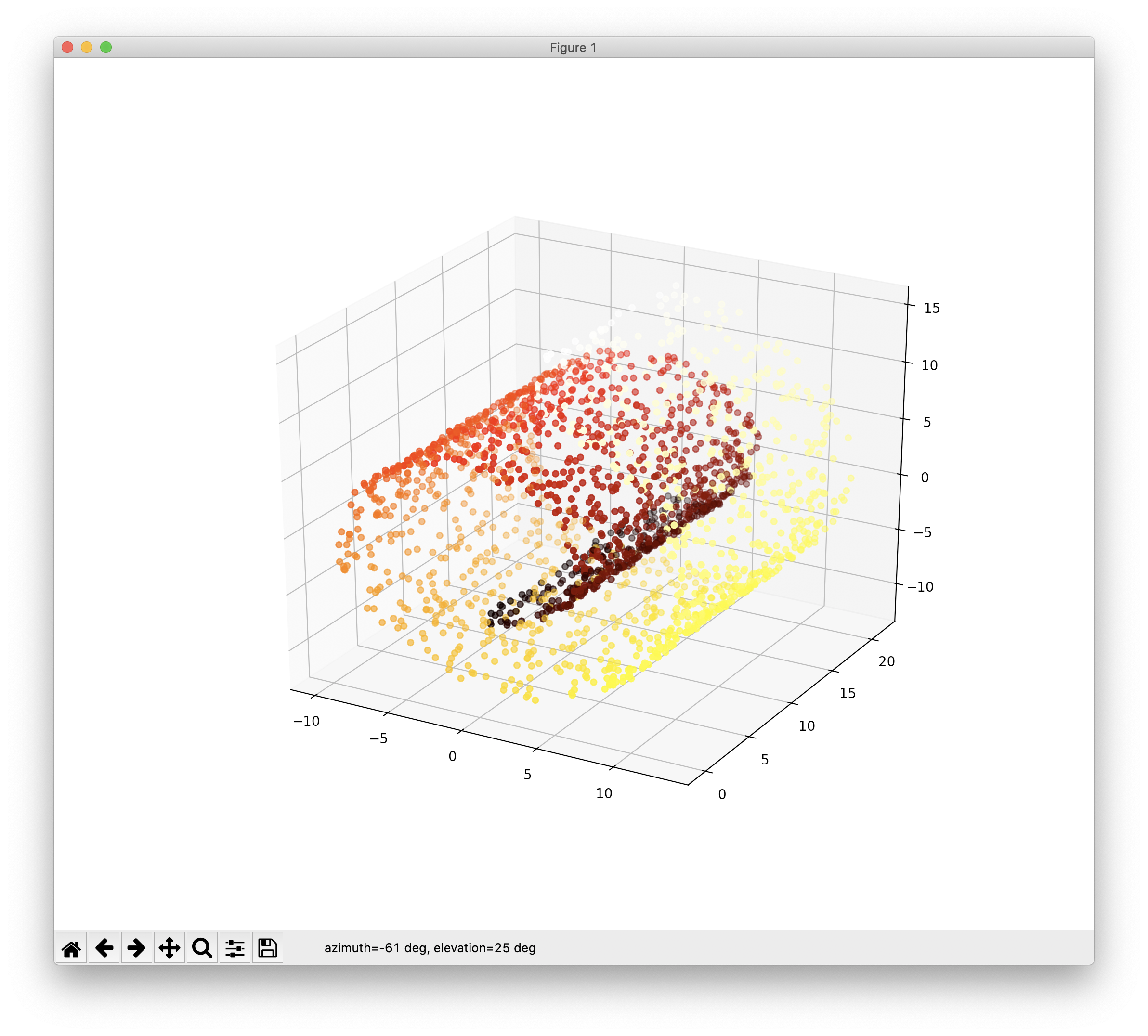
데이터는 사이킷런에서 제공하는 데이터셋 중 스위스롤로 스펀지 케익을 롤케익처럼 둘둘 말아 놓은 형태인데요, 이를 평면으로 펴서 시각화하는 코드와 그 결과는 다음과 같습니다.
plt.scatter(t, X[:, 1], c=t, cmap=plt.cm.hot)
plt.show()
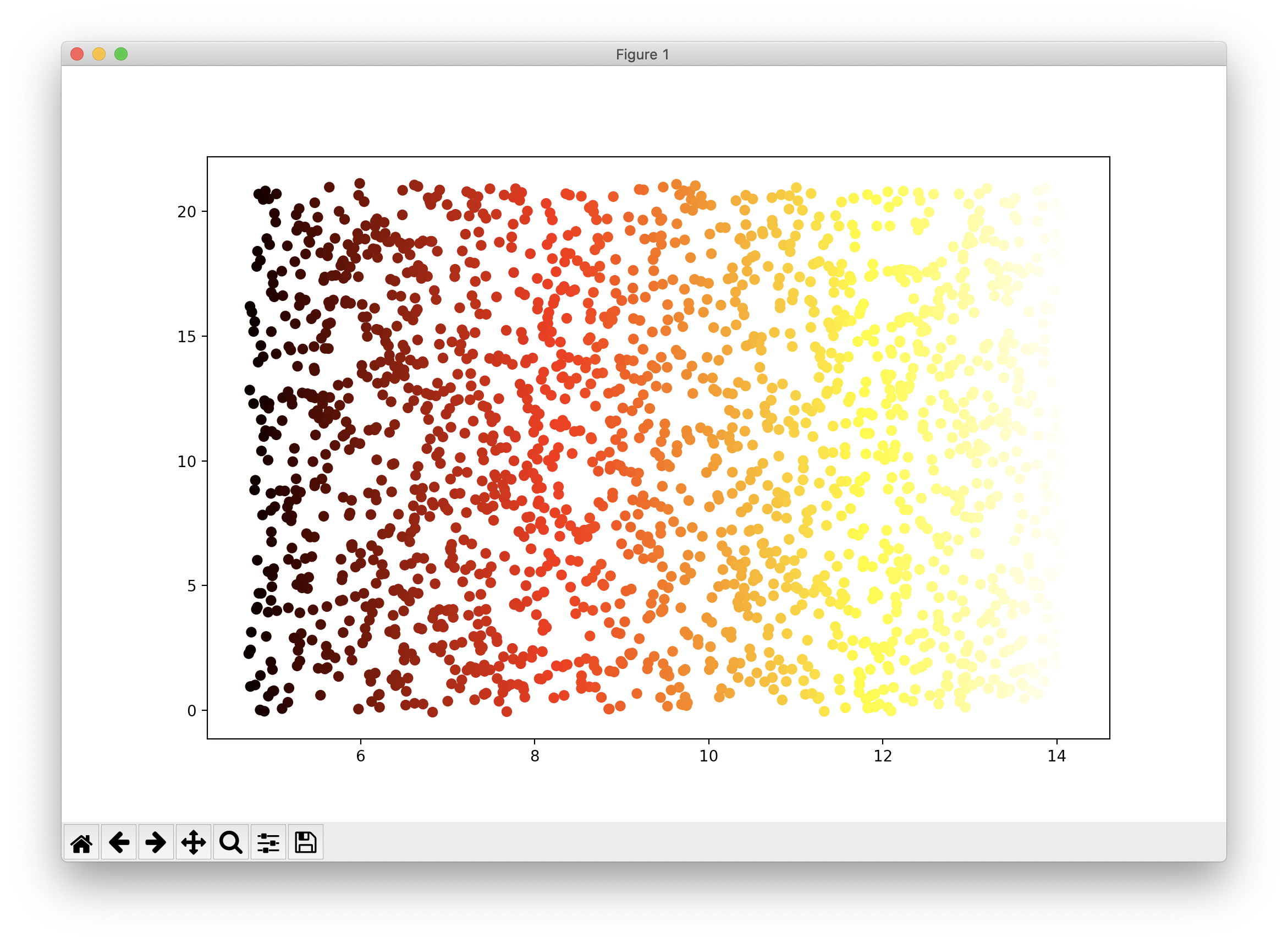
스위스롤 데이터셋에 대한 차원축소에 대한 최고의 결과는 바로 위의 결과라고도 할 수 있습니다. 하지만 이러한 해석은 2차원상의 시각화라는 관점에서만 국한된 결과입니다.
이제 실제 차원축소에 대한 다양한 방법을 코드로 살펴보겠습니다. 먼저 PCA입니다.
from sklearn.decomposition import PCA
X_pca_reduced = PCA(n_components=2, random_state=42).fit_transform(X)
plt.scatter(X_pca_reduced[:, 0], X_pca_reduced[:, 1], c=t, cmap=plt.cm.hot)
plt.show()
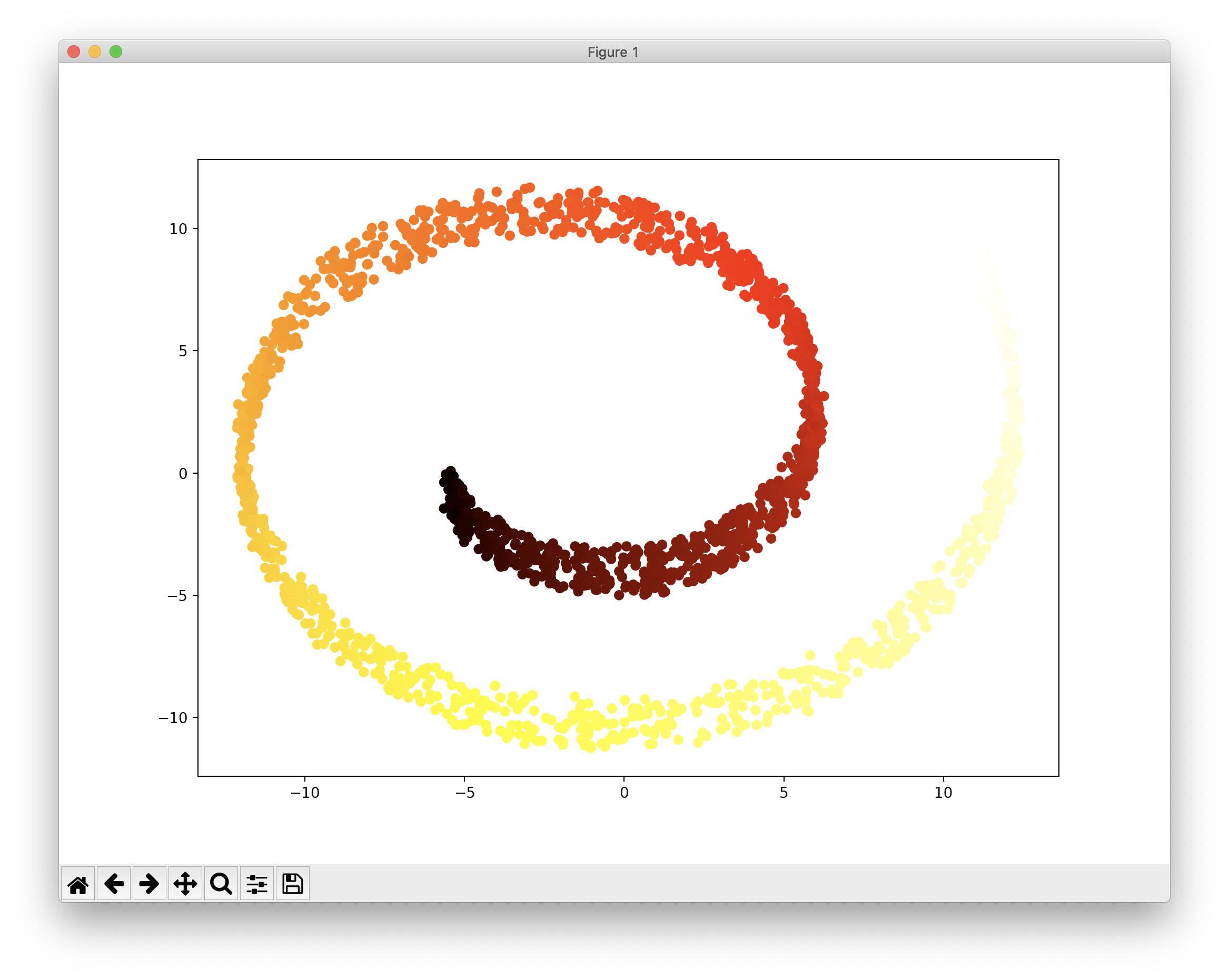
다음은 PCA의 비선형 버전인 Kernel PCA입니다.
from sklearn.decomposition import KernelPCA
lin_pca = KernelPCA(n_components=2, kernel="linear")
rbf_pca = KernelPCA(n_components=2, kernel="rbf", gamma=0.05)
sig_pca = KernelPCA(n_components=2, kernel="sigmoid", gamma=0.001, coef0=1)
plt.figure(figsize=(11, 4))
for subplot, pca, title in (
(131, lin_pca, "Linear kernel"),
(132, rbf_pca, "RBF kernel, $\gamma=0.05$"),
(133, sig_pca, "Sigmoid kernel, $\gamma=10^{-3}, r=1$")):
X_reduced = pca.fit_transform(X)
if subplot == 132:
X_reduced_rbf = X_reduced
plt.subplot(subplot)
plt.title(title, fontsize=14)
plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=t, cmap=plt.cm.hot)
plt.xlabel("$z_1$", fontsize=18)
if subplot == 131:
plt.ylabel("$z_2$", fontsize=18, rotation=0)
plt.show()
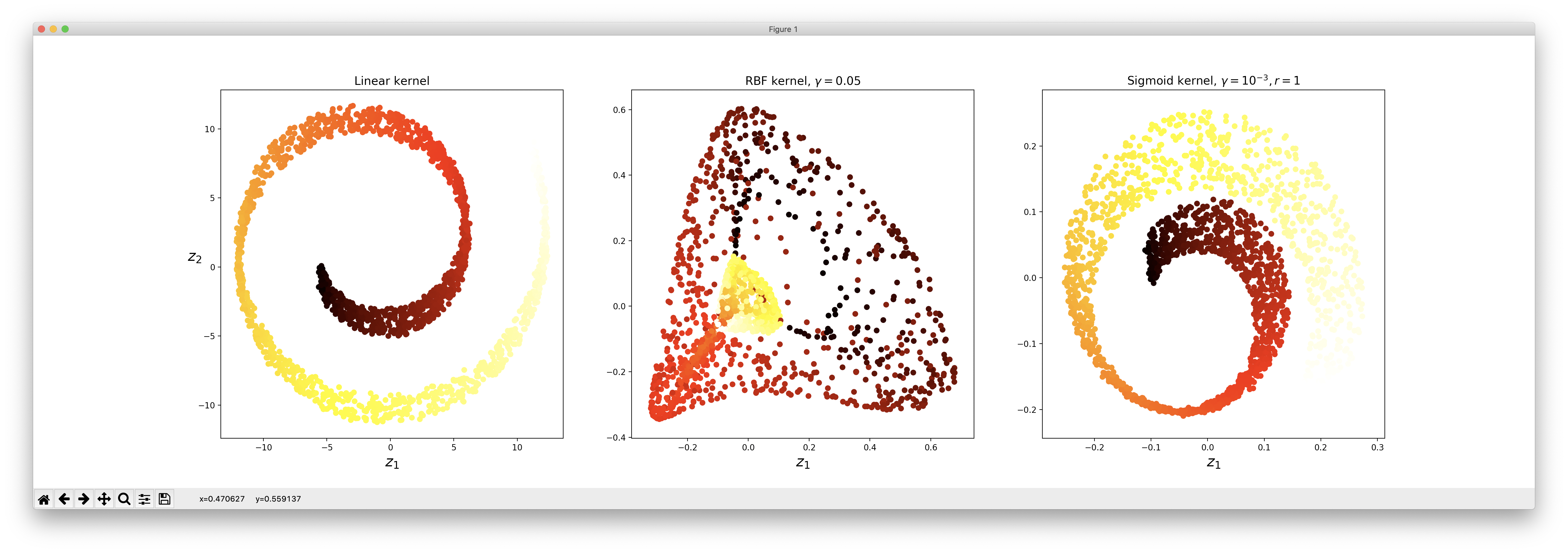
위의 코드는 3가지 종류의 커널에 대한 PCA 결과를 표현하고 있습니다.
다음은 LLE 알고리즘을 사용한 차원축소입니다. LLE는 Locally Linear Embedding으로 국소적인(지역적인) 샘플 데이터간 거리를 최대한 보존하며 차원을 축소합니다. 코드 및 그 결과는 아래와 같습니다.
from sklearn.manifold import LocallyLinearEmbedding
lle = LocallyLinearEmbedding(n_components=2, n_neighbors=10, random_state=3224)
X_reduced = lle.fit_transform(X)
plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=t, cmap=plt.cm.hot)
plt.show()
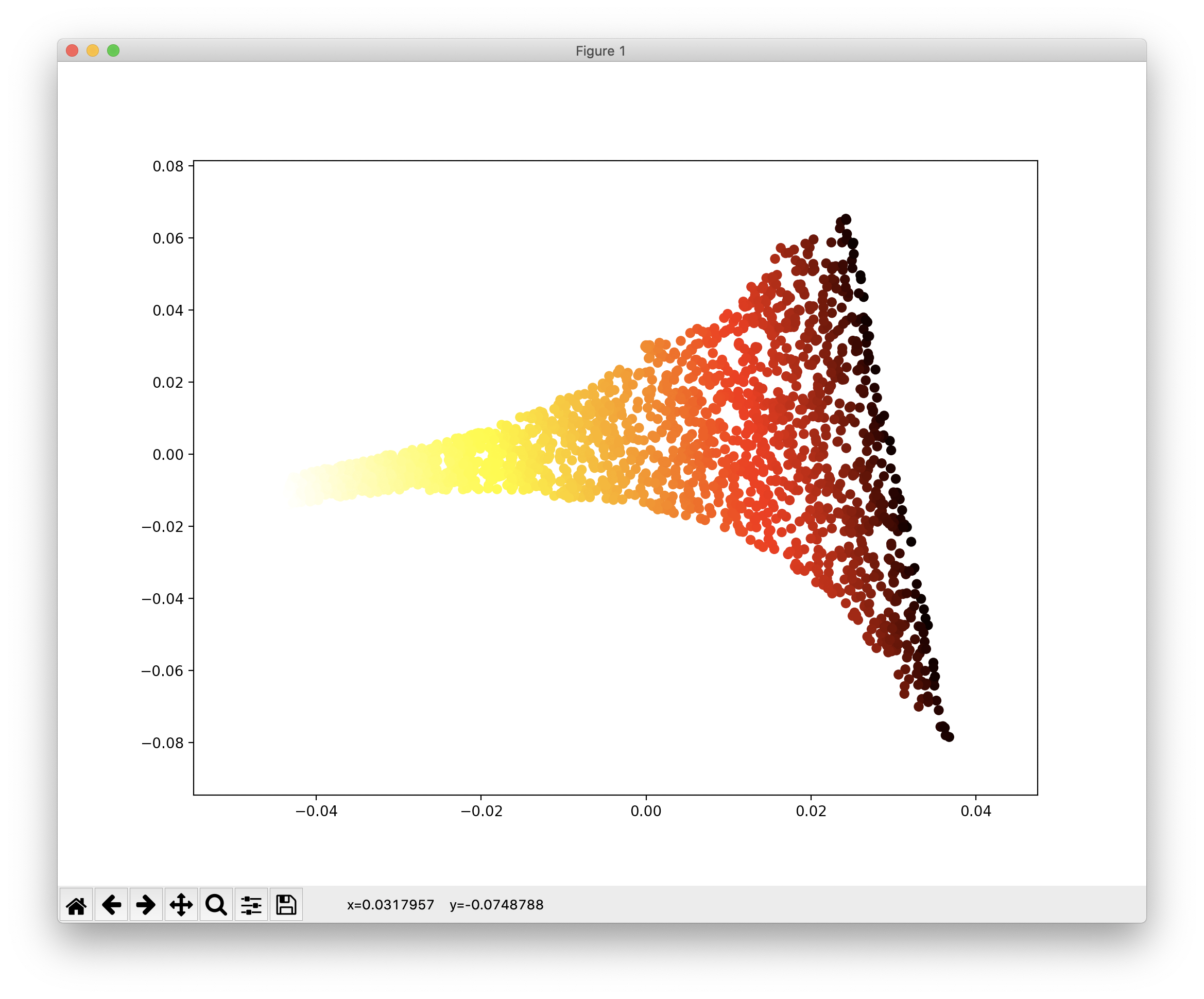
다음은 MDS로 다차원 스케일링(Multi-Dimensional Scaling)의 약자로, 샘플 데이터 간의 거리르 보존하면서 차원을 축소합니다. 코드 예와 그 결과는 다음과 같습니다.
from sklearn.manifold import MDS
mds = MDS(n_components=2, random_state=3224)
X_reduced_mds = mds.fit_transform(X)
plt.scatter(X_reduced_mds[:, 0], X_reduced_mds[:, 1], c=t, cmap=plt.cm.hot)
plt.show()
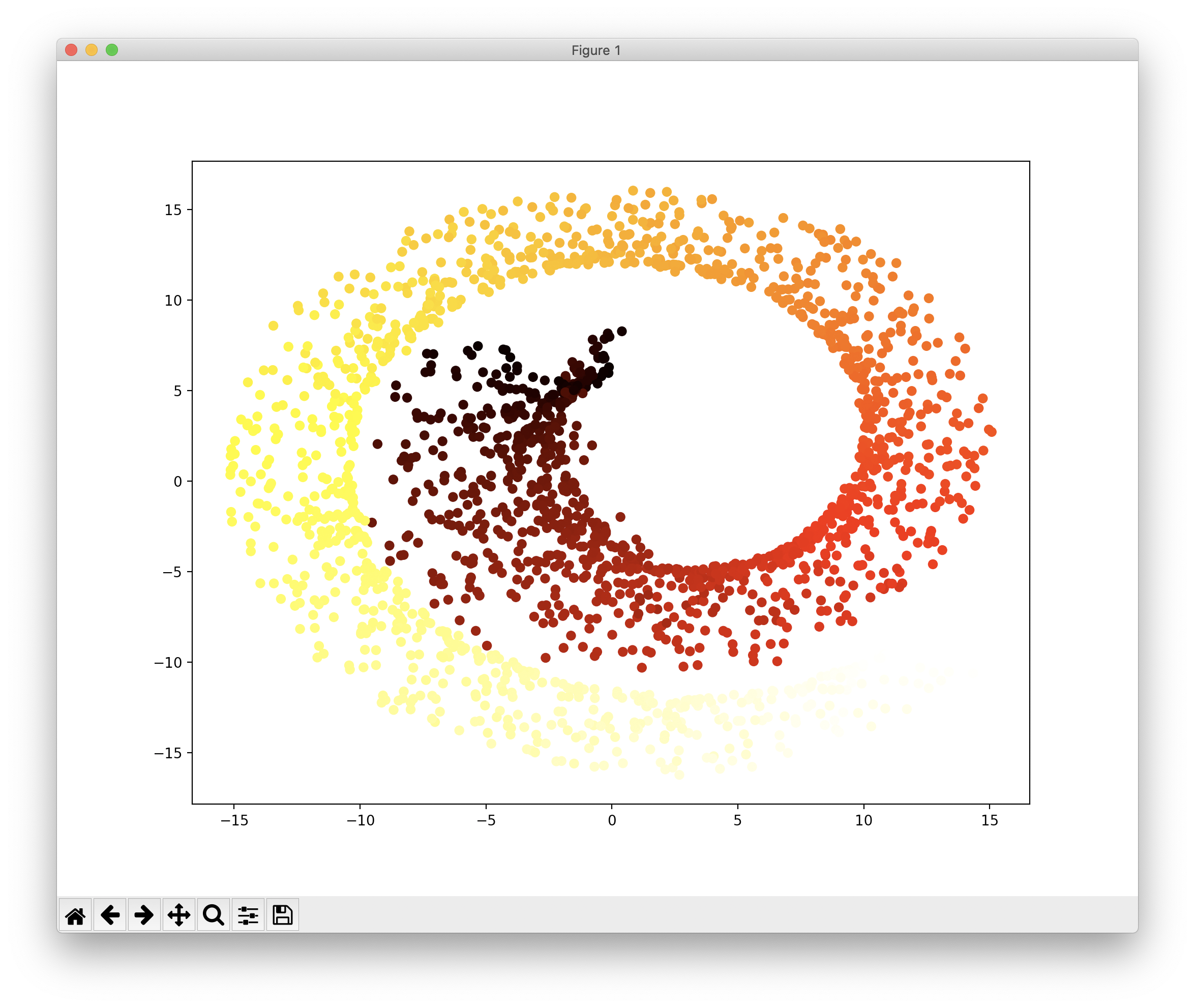
다음은 Isomap을 이용한 차원축소이며, 이는 각 샘플에서 가장 가까운 샘플 간의 거리, 보다 정확히는 Geodesic Distance를 유지하면서 차원을 축소합니다. 코드와 그 결과는 다음과 같습니다.
from sklearn.manifold import Isomap
isomap = Isomap(n_components=2)
X_reduced_isomap = isomap.fit_transform(X)
plt.scatter(X_reduced_isomap[:, 0], X_reduced_isomap[:, 1], c=t, cmap=plt.cm.hot)
plt.show()
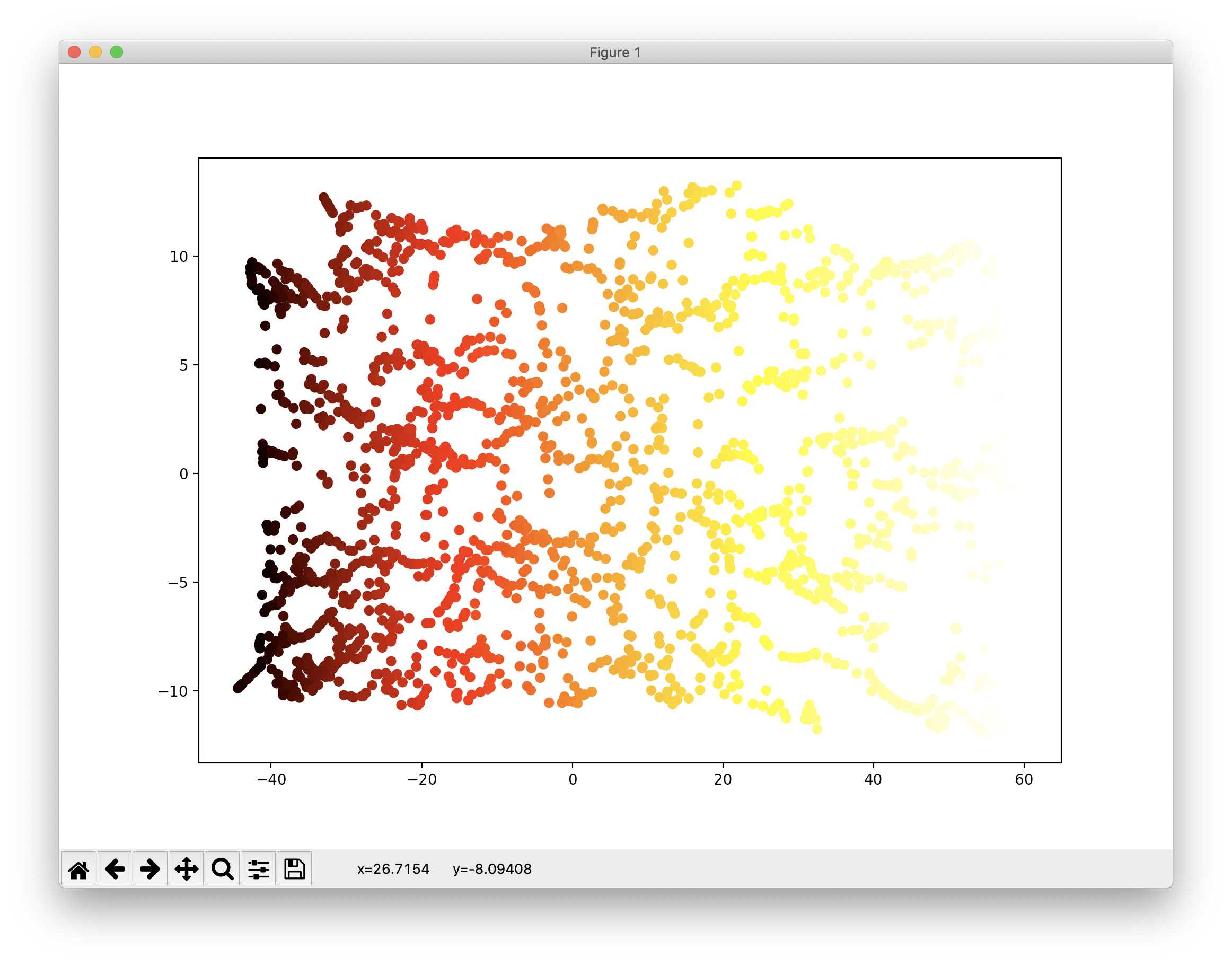
더 많은 차원축소 방법이 존재하지만 이 글에서는 마지막으로 t-SNE을 이용한 차원감소를 소개합니다. 주로 시각화에 많이 사용되며 군집화된 결과를 시각적으로 표현합니다. 코드와 결과는 다음과 같습니다.
from sklearn.manifold import TSNE
tsne = TSNE(n_components=2, random_state=3224)
X_reduced_tsne = tsne.fit_transform(X)
plt.scatter(X_reduced_tsne[:, 0], X_reduced_tsne[:, 1], c=t, cmap=plt.cm.hot)
plt.show()
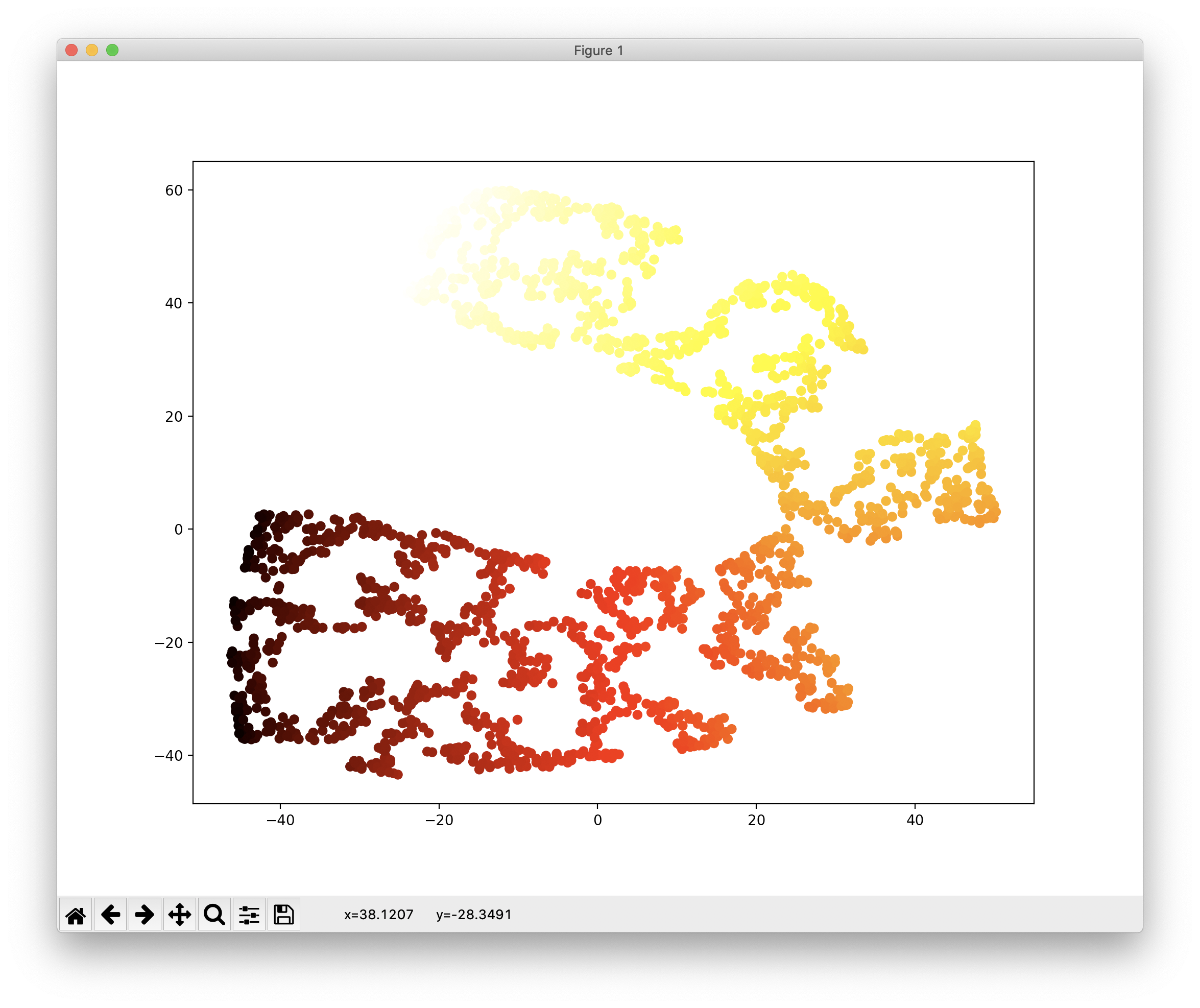
t-SNE를 이용한 다른 글은 아래의 링크를 참조하시기 바랍니다.
잠재벡터(Latent) z의 공간분포 시각화(Visualization)