WordNet은 프린스턴 대학교에서 구축한 유의어 DB인데, 유의어 사이의 관계를 그래프로 정의하고 있는 방대한 데이터입니다. 이 WordNet을 이용하여 유사한 단어를 파악할 수 있고, 각 단어의 유사도를 계산할 수 있습니다. 이를 파이썬의 NLTK를 이용해 활용할 수 있는데, 이에 대한 코드를 정리해 봅니다.
먼저 NLTK 패키지의 설치가 필요합니다. 제 환경에서는 conda install nltk와 같은 식으로 설치하였습니다.
NLTK 패키지의 설치가 끝나면 다음과 같은 코드를 통해 WordNet 데이터를 PC에 다운로드 받을 수 있습니다.
import nltk
nltk.download('wordnet')
가장먼저 ‘man’이라는 단어의 유의어를 검색하기 위해 다음 코드가 사용됩니다.
from nltk.corpus import wordnet
print(wordnet.synsets('man'))
''' Output:
[
Synset('man.n.01'),
Synset('man.n.03'),
Synset('man.n.05'),
Synset('man.n.06'),
Synset('man.n.08'),
Synset('man.n.09'),
Synset('man.n.10'),
Synset('man.v.01'),
Synset('man.v.02')],
Synset('serviceman.n.01'),
Synset('homo.n.02'),
Synset('valet.n.01'),
Synset('world.n.08')
]
'''
위의 검색에서 man.n.01의 경우 n은 명사를 의미합니다. 참고로 v는 동사이구요. 01은 man에 대한 인덱스값입니다. 이 man.n.01에 대한 사전적 의미를 얻기 위한 코드는 다음과 같습니다.
man = wordnet.synset('man.n.01')
print(man.definition()) # an adult person who is male (as opposed to a woman)
버그인지는 모르겠으나, man.n.02는 검색되지 않았음에도 아래의 코드는 유효합니다.
man2 = wordnet.synset('man.n.02')
print(man2.definition()) # someone who serves in the armed forces; a member of a military force
man.n.01에 대한 단어의 관계 그래프는 다음 코드를 통해 얻을 수 있습니다.
print(man.hypernym_paths())
''' Output:
[
[Synset('entity.n.01'), Synset('physical_entity.n.01'), Synset('causal_agent.n.01'), Synset('person.n.01'), Synset('adult.n.01'), Synset('man.n.01')],
[Synset('entity.n.01'), Synset('physical_entity.n.01'), Synset('object.n.01'), Synset('whole.n.02'), Synset('living_thing.n.01'), Synset('organism.n.01'), Synset('person.n.01'), Synset('adult.n.01'), Synset('man.n.01')],
[Synset('entity.n.01'), Synset('physical_entity.n.01'), Synset('causal_agent.n.01'), Synset('person.n.01'), Synset('male.n.02'), Synset('man.n.01')],
[Synset('entity.n.01'), Synset('physical_entity.n.01'), Synset('object.n.01'), Synset('whole.n.02'), Synset('living_thing.n.01'), Synset('organism.n.01'), Synset('person.n.01'), Synset('male.n.02'), Synset('man.n.01')]
]
'''
위의 관계 그래프 정보는 총 4개의 list로 구성된 list인데, 이를 시각화하면 다음과 같습니다.
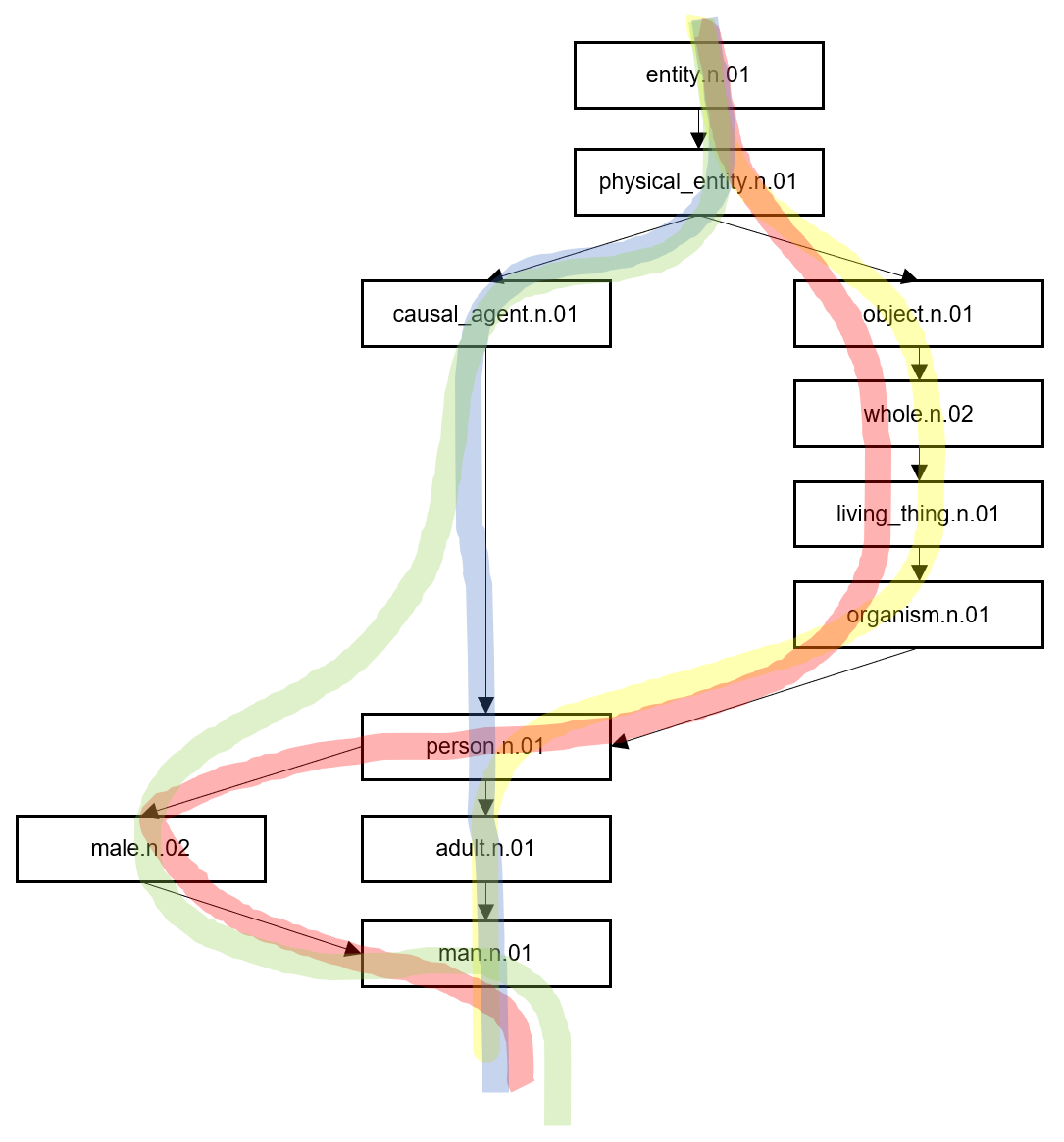
관계 그래프의 경로 역시 4개라는 것을 알 수 있고, 경로의 흐름에 따라 단어의 의미가 점점 구체화됩니다. 이 관계 그래프를 통해 서로 다른 단어에 대한 유사도를 계산할 수 있는데, 아래의 코드가 그 예입니다.
boy = wordnet.synset('boy.n.01')
guy = wordnet.synset('guy.n.01')
girl = wordnet.synset('girl.n.01')
woman = wordnet.synset('woman.n.01')
print(man.path_similarity(man)) # 1.0
print(man.path_similarity(boy)) # 0.3333333333333333
print(man.path_similarity(guy)) # 0.5
print(man.path_similarity(girl)) # 0.25
print(man.path_similarity(woman)) # 0.3333333333333333
단어 간의 유사도는 0부터 1까지의 값으로, 1에 가까울수록 두 단어의 의미가 더욱더 유사하다는 의미이고, 0에 가까울수록 그 의미의 관계가 거의 없다는 것을 의미합니다.
