이번장에서는 오랬동안 길게 끌어온 OpenGL의 렌더링 성능을 향상 시켜주는 Display List에 대해 알아보고자 한다. 사실 이 부분을 16장에 위치시키기에는 그 내용이 기본적이긴 하지만 필자 스스로의 혼란을 줄이기 위해 그냥 순서대로 번호를 매겼다. 이 강좌는 1장에 이여 두번째로 NeHe의 Display List를 그대로 번역한다. 이제 시작해 보자.
이번장에서는 오랬동안 길게 끌어온 OpenGL의 렌더링 성능을 향상 시켜주는 Display List에 대해 알아보고자 한다. 사실 이 부분을 16장에 위치시키기에는 그 내용이 기본적이긴 하지만 필자 스스로의 혼란을 줄이기 위해 그냥 순서대로 번호를 매겼다. 이 강좌는 1장에 이여 두번째로 NeHe의 Display List를 그대로 번역한다. 이제 시작해 보자.
이 강좌에서는 Display List에 대한 설명이다. 간단한 장면을 연출하고자 할때 Display List를 사용함으로써 속도의 개선 뿐만이 아니라 코드 줄수 또한 줄일 수 있다.
예를 들어서, 소행성 게임을 만들고 있다고 해 보자. 각 레벨은 최소한 2개 이상의 소행성으로 시작된다. 그래서 당신은 3차원의 소행성을 어떻게 만들 것인지 계산한다. 일단 계산이 끝난후 폴리곤이나 Quad를 이용하여 소행성을 만든다. 이 소행성이 여덜개의 면으로 이루어졌다고 해보자. 이렇게 만든 하나의 소행성을 여러개 만들기 위해, 간결하게 반복문을 이용하여 여러개의 소행성들을 그리게 될 것이다. 소행성을 만들기 위해 18줄 이상의 코드를 쳐 넣을 것이다. 소행성 하나 하나를 시스템 상에서 계산하여 매번 소행성을 그려내는 것은 비효율적이다. 소행성이 복잡하면 복잡할 수록 그 효율은 극적으로 떨어지게 된다.
그렇다면 그 해결책은 무엇인가? 바로 Display Lists이다. Display List를 사용함으로써, 소행성을 단 한번만 만들기만 하면 된다. 여기에 텍스쳐 맵핑을 할 수도 있고 색을 입힌다거나 원하는 모든 것들을 적용할 수 있다. 이 Display List에 이름을 부여할 수 있는데, 예를 들어 소행성의 Display List로 생성을 하고 이름을 ‘Asteroid’라고 한후에 나중에 소행성이 필요할때 마다 단지 이미 정해둔 이름인 ‘Asteroid’로써 Display List를 호출하기만 하면 된다. 즉, 앞으로 소행성을 그리고자 한다면 단지 단 한줄의 코드인 glCallList(asteroid)를 호출하기만 하면 된다. 이미 만들어진 소행성은 즉시 화면에 나타나게 된다. 소행성은 이미 Display List에서 모든 계산이 이루어져 생성되었기 때문에 OpenGL은 다시 소행성을 그리기 위해 계산할 필요가 없어진다. 이것은 메모리 상에 이미 계산의 결과를 저장해 놓았기 때문이다. 이것이 바로 왜 Dislpay List를 사용함으로써 속도가 극적으로 향상되는지하는지에 대한 해답니다.
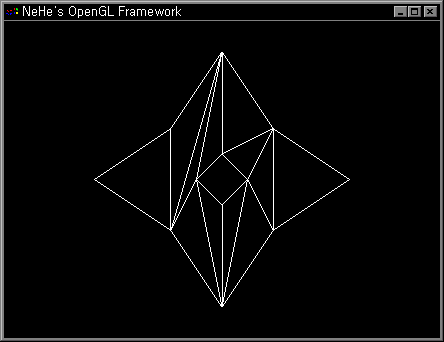
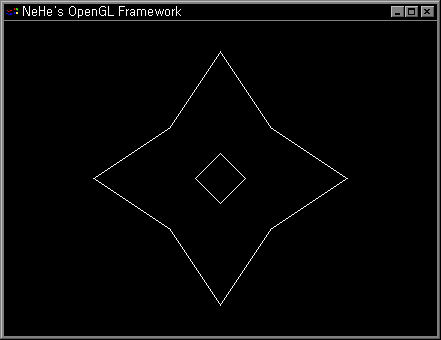
이제 Display List에 대해 배워볼 마음이 생기는가? 🙂 우리는 앞으로 Q-Bert Display List 데모 프로그램을 만들어 볼 것이다. 화면상에 15개의 큐브를 올려 놓아 보는 데모이다. 각각의 큐브는 BOX와 TOP으로 구성되져 있다. TOP은 별도의 Display List로서 만들어질 것인데 이것은 이 것에 좀더 어두운 색으로 연출하고자 함이다. BOX는 윗면이 없는 큐브이다.
이 코드는 강좌 6의 것을 사용한다. 무엇을 전달하고자 하는지를 쉽게 하기 위해 프로그램을 거의 전체적으로 다시 작성할 것이다. 다음의 코드 라인은 대부분의 강좌에서의 표준 코드들이다. (역자주: 강좌 6의 소스 코드를 일단 다운 로드 받아 살펴보기 바란다. 단지 텍스쳐 맵핑에 대한 내용을 다룬 것이다.)
#include // Header File For Windows
#include // Header File For Standard Input/Output
#include // Header File For The OpenGL32 Library
#include // Header File For The GLu32 Library
#include // Header File For The GLaux Library
HDC hDC=NULL; // Private GDI Device Context
HGLRC hRC=NULL; // Permanent Rendering Context
HWND hWnd=NULL; // Holds Our Window Handle
HINSTANCE hInstance; // Holds The Instance Of The Application
bool keys[256]; // Array Used For The Keyboard Routine
bool active=TRUE; // Window Active Flag Set To TRUE By Default
bool fullscreen=TRUE; // Fullscreen Flag Set To Fullscreen Mode By Default
이제, 앞으로 사용할 변수를 선언해 보자. 먼저 하나의 텍스쳐를 저장하기 위한 변수를 선언하고 앞에서 언급한 2개의 Display List를 위한 변수 2개를 선언하자. 이러한 변수는 Display List가 램에서 어디에 저장되어 있는가 하는 지시자로써의 행동한다. 이 2개의 Display List를 BOX와 TOP이라 부를 것이다.
2개의 변수를 선언한 후에 xloop와 yloop라는 변수를 선언하는데 이것은 화면상의 큐브를 위치시키는데 사용된다. 또 xrot와 yrot라는 2개의 변수를 선언하는데 이것은 x와 y축으로 큐브들을 회전시키는데 사용되는 변수들이다.
GLuint texture[1]; // Storage For One Texture
GLuint box; // Storage For The Display List
GLuint top; // Storage For The Second Display List
GLuint xloop; // Loop For X Axis
GLuint yloop; // Loop For Y Axis
GLfloat xrot; // Rotates Cube On The X Axis
GLfloat yrot; // Rotates Cube On The Y Axis
다음에 우리는 2개의 색상 배열을 생성한다. 첫번째의 boxcol은 밝은 계열의 색상들로 빨간색, 오랜지색, 초록색 그리고 파란색의 색상값을 저장한다. {}안에 지정된 각각의 값은 Red, Green Blue 값을 나타낸다. 각각의 {}의 구룹은 지정된 색이다.
두번째 색상의 배열은 어두운 계열의 색상들로 빨간색, 오랜지색, 초록색 그리고 파란색을 위한 것이다. 어두운 색들은 박스의 윗면을 나타내는데 사용된다. 우리는 박스의 나머지 부분보다 박스의 뚜껑을 좀더 어둡게 하고자 한다.
static GLfloat boxcol[5][3]= // Array For Box Colors
{// Bright: Red, Orange, Yellow, Green, Blue
{1.0f,0.0f,0.0f},
{1.0f,0.5f,0.0f},
{1.0f,1.0f,0.0f},
{0.0f,1.0f,0.0f},
{0.0f,1.0f,1.0f}};
static GLfloat topcol[5][3]= // Array For Top Colors
{ // Dark: Red, Orange, Yellow, Green, Blue
{.5f,0.0f,0.0f},
{0.5f,0.25f,0.0f},
{0.5f,0.5f,0.0f},
{0.0f,0.5f,0.0f},
{0.0f,0.5f,0.5f}};
// Declaration For WndProc
LRESULT CALLBACK WndProc(HWND, UINT, WPARAM, LPARAM);
이제 실제 Display List를 만들어 본다. 이미 짐작했겠지만, 박스를 만들기 위한 모든 코드는 첫번째 List로 하고 뚜껑으로 사용할 박스의 Top은 다른 List에 들어가게 된다. 다음 절에서 더 자세한 내용을 설명하도록 하겠다.
GLvoid BuildLists() // Build Box Display List
{
우리는 OpenGL에게 우리가 2개의 List를 필요로 한다고 알리는 것으로 시작한다. glGenLists(2)는 두개의 List를 위한 공간을 생성하고 첫번재 List를 가르키는 포인터를 반환한다. box가 첫번째 List의 위치를 가지게 된다. 언제든지 box를 호출한다면 첫번째 list에 담긴 물체가 그려지게 된다.
box=glGenLists(2); // Building Two Lists
List를 위한 공간을 마련했으므로 실제 List를 생성해 보자. 우리는 이미 두개의 List를 위한 메모리 공간을 마련했고 box가 첫번째 list를 저장하는 공간을 가르킨다는 것을 알고 있다. 이제 OpenGL에게 알려할 모든 것은 리스드가 어디로 가야하며 만들어질 리스트가 어떤 타입인가 하는 것들이다.
작업을 하기 위해 glNewList() 명령을 사용한다. 우리는 첫번째 인자가 box라는 것을 알게 될 것이다. 이것은 box가 가르키고 있는 메모리의 위치에 리스트가 저장되어져 있다고 openGL에게 알리는 것이다. 두번째 인자인 GL_COMPILE는 OpenGL에게 우리가 메모리 상에 모든 계산을 미리 해 놓으라는 지시인데 이렇게 함으로써 나중에 다시 불피요한 재계산을 하지 않아도 되도록 하는 것이다.
GL_COMPILE은 프로그래밍과 유사하다. 프로그램을 작성한다면 컴파일러에 적재해야 한다. 코드를 실행하기 위해서 매번 컴파일을 해야 한다. 코드가 이미 실행파일 형태로 컴파일 되어있다면 이후부터 컴파일 할 필요없이 실행파일만을 클릭하여 실행하기만 하면 된다. 컴파일이 필요없는 것이다. 일단 GL이 display list를 컴파일했다면 이미 렌더링 준비가 되어진 것이고 나중에 또 컴파일이 요구되지 않는다. 이것이 바로 display list를 사용함으로써 속도를 향상시키는 이유이다.
glNewList(box,GL_COMPILE); // New Compiled box Display List
코드의 다음부는 뚜껑(top)이 없는 박스를 그리는 것이다. 이것은 화면상에 나타나지 않고 단지 display list상에 저장된다.
glNewList()와 glEndList()사이에 당신이 원하는 코드들을 추가할 수 있다. 색상을 설정하거나 텍스쳐 맵핑을 바꾼다거나 하는 것등. 추가할 수 없는 유일한 코드는 list에 지정된 객체의 형태를 변경시키는 코드이다. 일단 list로 만들어지면 변경할 수 없다.
만약 glColor3ub(rand()%255, rand()%255, rand()%255)의 코드를 아래에 제시한 코드에 추가했다면, 아마도 당신은 화면상에 물체가 그려지는 때마다 이것의 색이 바뀐다고 생각할 것이다. 그러나 이미 리스트를 생성할때 색상이 지정되졌기 때문에 색은 변경되지 않는다. (역자주: 만약 변경하고자 한다면 list를 생성할때 색상을 지정하는 코드를 사용해서는 않된다)
glBegin(GL_QUADS); // Start Drawing Quads
// Bottom Face
// - Top Right Of The Texture and Quad
glTexCoord2f(1.0f, 1.0f); glVertex3f(-1.0f, -1.0f, -1.0f);
// - Top Left Of The Texture and Quad
glTexCoord2f(0.0f, 1.0f); glVertex3f( 1.0f, -1.0f, -1.0f);
// - Bottom Left Of The Texture and Quad
glTexCoord2f(0.0f, 0.0f); glVertex3f( 1.0f, -1.0f, 1.0f);
// - Bottom Right Of The Texture and Quad
glTexCoord2f(1.0f, 0.0f); glVertex3f(-1.0f, -1.0f, 1.0f);
// Front Face
// - Bottom Left Of The Texture and Quad
glTexCoord2f(0.0f, 0.0f); glVertex3f(-1.0f, -1.0f, 1.0f);
// - Bottom Right Of The Texture and Quad
glTexCoord2f(1.0f, 0.0f); glVertex3f( 1.0f, -1.0f, 1.0f);
// - Top Right Of The Texture and Quad
glTexCoord2f(1.0f, 1.0f); glVertex3f( 1.0f, 1.0f, 1.0f);
// - Top Left Of The Texture and Quad
glTexCoord2f(0.0f, 1.0f); glVertex3f(-1.0f, 1.0f, 1.0f);
// Back Face
// - Bottom Right Of The Texture and Quad
glTexCoord2f(1.0f, 0.0f); glVertex3f(-1.0f, -1.0f, -1.0f);
// - Top Right Of The Texture and Quad
glTexCoord2f(1.0f, 1.0f); glVertex3f(-1.0f, 1.0f, -1.0f);
// - Top Left Of The Texture and Quad
glTexCoord2f(0.0f, 1.0f); glVertex3f( 1.0f, 1.0f, -1.0f);
// - Bottom Left Of The Texture and Quad
glTexCoord2f(0.0f, 0.0f); glVertex3f( 1.0f, -1.0f, -1.0f);
// Right face
// - Bottom Right Of The Texture and Quad
glTexCoord2f(1.0f, 0.0f); glVertex3f( 1.0f, -1.0f, -1.0f);
// - Top Right Of The Texture and Quad
glTexCoord2f(1.0f, 1.0f); glVertex3f( 1.0f, 1.0f, -1.0f);
// - Top Left Of The Texture and Quad
glTexCoord2f(0.0f, 1.0f); glVertex3f( 1.0f, 1.0f, 1.0f);
// - Bottom Left Of The Texture and Quad
glTexCoord2f(0.0f, 0.0f); glVertex3f( 1.0f, -1.0f, 1.0f);
// Left Face
// - Bottom Left Of The Texture and Quad
glTexCoord2f(0.0f, 0.0f); glVertex3f(-1.0f, -1.0f, -1.0f);
// - Bottom Right Of The Texture and Quad
glTexCoord2f(1.0f, 0.0f); glVertex3f(-1.0f, -1.0f, 1.0f);
// - Top Right Of The Texture and Quad
glTexCoord2f(1.0f, 1.0f); glVertex3f(-1.0f, 1.0f, 1.0f);
// - Top Left Of The Texture and Quad
glTexCoord2f(0.0f, 1.0f); glVertex3f(-1.0f, 1.0f, -1.0f);
glEnd(); // Done Drawing Quads
우리는 List를 다 만들었다는 것을 OpenGL에게 알리기 위해 glEndList() 명령을 내린다. glNewList()와 glEndList() 사이의 부분은 Display list의 부분이다. glNewList() 앞의 부분이나 glEndList()의 뒷부분은 현재 display list의 부분과는 상관없는 부분이다.
glEndList(); // Done Building The box List
이제, 두번째 Display list를 만들 것이다. 두번째 display list가 메모리에 저장될 곳을 찾기 위해 우리는 예전의 display list(box)에 1을 추가한다. 아래의 코드는 두번째 display list의 위치와 같은 ‘top’을 만들 것이다.
top=box+1; // top List Value Is box List Value +1
이제 두번째 display list을 저장할 곳을 알았으므로 뚜껑에 대한 list를 만들 수 있다. 첫번재 list를 만드는 같은 방법을 사용하지만 이번에는 ‘box’대신 ‘top’에 list를 저장한다고 OpenGL에게 알린다.
glNewList(top,GL_COMPILE); // New Compiled top Display List
다음 코드는 단지 박스의 꼭대기를 그려주는 것이다. Z 평면 상의 간단한 사각형이다.
glBegin(GL_QUADS); // Start Drawing Quad
// Top Face
// - Top Left Of The Texture and Quad
glTexCoord2f(0.0f, 1.0f); glVertex3f(-1.0f, 1.0f, -1.0f);
// - Bottom Left Of The Texture and Quad
glTexCoord2f(0.0f, 0.0f); glVertex3f(-1.0f, 1.0f, 1.0f);
// - Bottom Right Of The Texture and Quad
glTexCoord2f(1.0f, 0.0f); glVertex3f( 1.0f, 1.0f, 1.0f);
// - Top Right Of The Texture and Quad
glTexCoord2f(1.0f, 1.0f); glVertex3f( 1.0f, 1.0f, -1.0f);
glEnd(); // Done Drawing Quad
다시 우리는 OpenGL에게 두번째 list를 생성했다고 glEndList() 명령을 이용해 알린다. 바로 아래처럼. 우리는 성공적으로 2개의 display list를 생성했다.
glEndList(); // Done Building The top Display List
}
비트맵/텍스쳐를 생성하는 코드는 이전에 강좌의 비트맵을 로딩하고 텍스쳐를 생성하는 코드와 같다. (역자주: Dip2K의 튜터리얼도 NeHe의 텍스쳐 맵핑 방법과 동일하다. 우리는 각각의 큐브의 모든 6면 상에 맵핑할 텍스쳐를 원한다.좀더 부드러운 텍스쳐 맵핑을 위해 Mipmapping을 사용하고자 한다. 필자는 픽셀을 보는 것을 무척 싫어한다. (역자주: 픽셀을 본다는 것은 알리아싱 현상을 의미한다) ‘cube.bmp’라는 비트맵을 로딩한다. data 디렉토리에 이 비트맵 파일이 위치한다. LoadBMP 함수를 찾아서 다음과 같이 수정한다.
if (TextureImage[0]=LoadBMP("Data/Cube.bmp")) // Load The Bitmap
폼의 크기가 재조정될때 발생하는 이벤트의 코드는 강좌 6의 코드와 동일하다.
init 코드는 약간의 수정만이 필요하다. BuildList() 코드를 추가한다. 이것은 앞에서 display list를 생성하는 코드를 담고 있다. LoadGLTextures()함수 이후에 BuildList() 를 호출한다는 것에 주의해야 한다. 이것은 BuildList() 함수에서 텍스처를 필요로 하므로 먼저 텍스쳐를 생성해야 한다는 것이다.
int InitGL(GLvoid) // All Setup For OpenGL Goes Here
{
if (!LoadGLTextures()) // Jump To Texture Loading Routine
{
return FALSE; // If Texture Didn't Load Return FALSE
}
BuildLists(); // Jump To The Code That Creates Our Display Lists
glEnable(GL_TEXTURE_2D); // Enable Texture Mapping
glShadeModel(GL_SMOOTH); // Enable Smooth Shading
glClearColor(0.0f, 0.0f, 0.0f, 0.5f); // Black Background
glClearDepth(1.0f); // Depth Buffer Setup
glEnable(GL_DEPTH_TEST); // Enables Depth Testing
glDepthFunc(GL_LEQUAL); // The Type Of Depth Testing To Do
다음의 세줄의 코드는 quick & dirty 빛을 활성화 하는 것이다. (역자주: quick & dirty 광원은 비디오 카드에 기본적으로 설정된 광원이다) Light0는 대부분의 비디오 카드에 미리 정의된 것이다. light0을 활성화 함으로써 빛을 사용한다. 만약 독자의 비디오 카드에서 light0가 작동하지 않는다면(화면에 마냥 검다면) 그냥 광원을 꺼라.마지막 라인인 GL_COLOR_MATRIAL은 텍스쳐 맵핑에 색을 추가하도록 해 준다. 이 재질의 컬러링을 가능하지 않게 한다면, 텍스쳐는 항상 원래의 색상으로 나타난다. 즉 glColor3f(r,g,b)가 아무런 효과를 내지 못한다. 그래서 이것을 가능하게 해주는 것이 중요하다.
glEnable(GL_LIGHT0); // Quick And Dirty Lighting (Assumes Light0 Is Set Up)
glEnable(GL_LIGHTING); // Enable Lighting
glEnable(GL_COLOR_MATERIAL); // Enable Material Coloring
최종적으로 멋지게 보이도록 하기 위해서 투영에 대한 힌트를 GL에게 제공하고 초기화가 잘되었음을 알리기 위해 TRUE를 반환한다.
// Nice Perspective Correction
glHint(GL_PERSPECTIVE_CORRECTION_HINT, GL_NICEST);
return TRUE; // Initialization Went OK
이제 그려주는 코드에 대한 것이다. 일단 화면과 Depth Buffer를 청소하는 일부터 시작한다.
그 다음에 큐브에 텍스쳐 맵핑을 바인드한다. Display list 안에 이 텍스쳐 맵핑을 추가할 수 있었으나 그 밖으로 빼 놓았다. 이것으로써 원한다면 언제든 텍스쳐 맵핑을 변경할 수 있는 것이다. (역자주: 이미 앞에서 언급한대로 List를 만들때 색상이라든지 텍스쳐 맵핑을 지정하면 나중에 그 List의 객체의 색상, 텍스쳐 맵핑을 변경할 수 없다)
int DrawGLScene(GLvoid) // Here's Where We Do All The Drawing
{
// Clear The Screen And The Depth Buffer
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glBindTexture(GL_TEXTURE_2D, texture[0]); // Select The Texture
이제 재미있는 것에 대해 살펴보자. yloop라 불리는 반복문이 있다. 이 반복문은 큐브들의 Y 축상(위에서 아래)에 위치시키는데 사용된다. 위에서 아래로 5개의 큐브를 원하므로 6보다 하나 작은 반복을 한다(즉, 다섯번)
for (yloop=1;yloop<6;yloop++) // Loop Through The Y Plane
{
xloop라는 다른 반복문이 있다. 이것은 X 축상(왼쪽에서 오른쪽)에 큐브들을 위치시키는데 사용된다. 왼쪽에서 오른쪽으로 그리고자 하는 큐브는 정해져 있지 않다. 만약 가장 위쪽의 줄이라면 xloop는 0에서 1까지의 xloop 반복이면 된다. 그리고 그 다음 줄의 xloop는 0에서 2가 될것이다(즉, 2개의 큐브가 그려져야 한다) (역자주: 계속 하나씩 증가한다, 실제 결과 프로그램을 실행하여 살펴보면 확실히 알수있다)
// Loop Through The X Plane
for (xloop=0;xloop {
glLoadIdentity()를 호출함으로써 View를 초기화한다.
glLoadIdentity(); // Reset The View
다음은 화면상의 지정된 지점으로 이동시키는 코드이다. 이것은 다소 헤깔리지만 실제로는 그렇지 않다. X축 상에서, 다음의 내용이 이뤄진다 :
큐브들이 모여 이뤄진 피라미드가 화면상의 중심에 놓여지도록 오른쪽으로 1.4 유닛만큼 이동한다. 그 다음에 xloop에 2.8을 곱한후 다시 여기에 1.4를 더한다. 마지막으로 yloop*1.4를 뺀다. 이것은 큐브들을 그들이 위치한 줄에 따라 왼쪽으로 이동하게 된다.
Y축상에서 6에서 yloop를 뺌으로써 아래 방향으로 피라미드가 만들어진다. 다음에 그 결과에 2.4를 곱한다. 큐브들은 y축 상의 각각의 꼭대기 상에 놓여진다. 다음에 7을 빼는데 이것은 피라미드가 화면의 아래쪽에서 시작하고 윈쪽으로 만들어지게 한다.
최종적으로 Z축 상에서 화면 안쪽으로 20 유닛 이동한다. 이것은 피라미드를 멋지게 만든다.
// Position The Cubes On The Screen
glTranslatef(1.4f+(float(xloop)*2.8f)-(float(yloop)*1.4f),
((6.0f-float(yloop))*2.4f)-7.0f,-20.0f);
이제 x축 상으로 회전시켜 보자. 우리는 큐브를 뷰쪽으로 45도에서 yloop*2를 뺀 상태로 기울인다.. 퍼스펙티브 모드는 자동으로 큐브들을 기울이므로 이 기울어짐을 제거 했다. 이것은 최선은 아니지만 원하는대로 작동한다. 🙂
최종적으로 xrot를 더한다. 이것은 키보드를 통해 각을 조정할 수있도록 한다.
x축으로 회전한후에 y축상으로 45도 회전하고 yrot을 더하는데 이것은 키보드를 통해서 yrot값을 조정할 수 있다.
glRotatef(45.0f-(2.0f*yloop)+xrot,1.0f,0.0f,0.0f); // Tilt The Cubes Up And Down
glRotatef(45.0f+yrot,0.0f,1.0f,0.0f); // Spin Cubes Left And Right
다음에 큐브들이 위치한 줄에 따라 달리 색상을 지정한다.
glColor3fv(boxcol[yloop-1]); // Select A Box Color
이제 박스에 대한 List를 호출한다.
glCallList(box); // Draw The Box
큐브의 꼭대기에 놓여질 뚜껑의 색상을 지정한다.
glColor3fv(topcol[yloop-1]); // Select The Top Color
뚜껑에 대한 List를 호출하고 모든것이 잘되었으므로 TRUE를 호출한다.
glCallList(top); // Draw The Top
}
}
return TRUE; // Jump Back
}
이제 남은 코드들은 WinMain 함수에서 이뤄지는데 다음은 키보드에 대해 xrot와 yrot의 값을 변경해 주는 키보드 입력 처리 코드이다. SwapBuffer(hDC) 코드 다음에 놓여진다.
SwapBuffers(hDC); // Swap Buffers (Double Buffering)
if (keys[VK_LEFT]) // Left Arrow Being Pressed?
{
yrot-=0.2f; // If So Spin Cubes Left
}
if (keys[VK_RIGHT]) // Right Arrow Being Pressed?
{
yrot+=0.2f; // If So Spin Cubes Right
}
if (keys[VK_UP]) // Up Arrow Being Pressed?
{
xrot-=0.2f; // If So Tilt Cubes Up
}
if (keys[VK_DOWN]) // Down Arrow Being Pressed?
{
xrot+=0.2f; // If So Tilt Cubes Down
}
<변역 끝>
변역을 여기서 끝마친다. 사실 이 강좌는 Display List에 대한 장이다. Display List에 대한 사용법이 쉽다는 것을 알 수 있다. 필자는 이 강좌를 번역할때 List를 제작하고 사용하는 방법에 대해서는 최대한 모든내용을 번역했지만 후반부의 큐브를 화면상에 피라미드 모양으로 위치시키는 세세한 내용은 그냥 술~ 술~ 넘기며 번역했음을 고백한다.

 빌보드 기법이란 사각형이 항상 시점을 바라보도록 만드는 것을 말한다. 결과적으로 관찰자가 어느 위치로 이동하더라도 사각형은 항상 같은 면을 관찰자에게 보여주게 된다. 응용예로써 넓은 대지위에 나무를 나타내고자 할때, 나무를 메쉬(Mesh)를 사용하여 모델링하지 않고 나무 이미지만으로 구현이 가능하다.
빌보드 기법이란 사각형이 항상 시점을 바라보도록 만드는 것을 말한다. 결과적으로 관찰자가 어느 위치로 이동하더라도 사각형은 항상 같은 면을 관찰자에게 보여주게 된다. 응용예로써 넓은 대지위에 나무를 나타내고자 할때, 나무를 메쉬(Mesh)를 사용하여 모델링하지 않고 나무 이미지만으로 구현이 가능하다.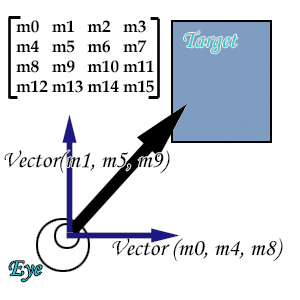 시선과 위쪽으로 수직인 벡터를 UpVector라 하고 오른쪽 방향으로 수직인 벡터를 RightVector라 하자. 이 두 벡터를 이용하여 사각형을 이루는 4개의 좌표를 조정하기 위해, 사각형의 중심 벡터를 centerVector라고 하면, 사각형을 이루는 4개의 좌표는 다음 그림과 같다.
시선과 위쪽으로 수직인 벡터를 UpVector라 하고 오른쪽 방향으로 수직인 벡터를 RightVector라 하자. 이 두 벡터를 이용하여 사각형을 이루는 4개의 좌표를 조정하기 위해, 사각형의 중심 벡터를 centerVector라고 하면, 사각형을 이루는 4개의 좌표는 다음 그림과 같다. 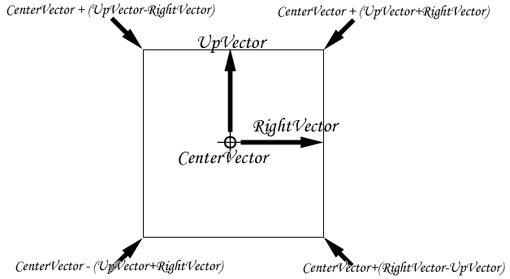 위의 네 좌표를 스칼라값 Size를 적용하면 다음과 같다. Size는 사각형의 크기로 생각할 수 있다.
위의 네 좌표를 스칼라값 Size를 적용하면 다음과 같다. Size는 사각형의 크기로 생각할 수 있다.

 이번장에서는 오랬동안 길게 끌어온 OpenGL의 렌더링 성능을 향상 시켜주는 Display List에 대해 알아보고자 한다. 사실 이 부분을 16장에 위치시키기에는 그 내용이 기본적이긴 하지만 필자 스스로의 혼란을 줄이기 위해 그냥 순서대로 번호를 매겼다. 이 강좌는 1장에 이여 두번째로 NeHe의 Display List를 그대로 번역한다. 이제 시작해 보자.
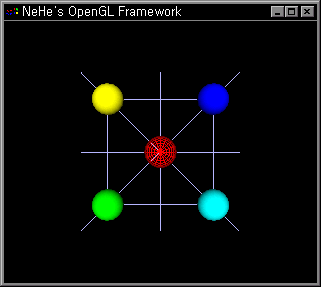
이번장에서는 오랬동안 길게 끌어온 OpenGL의 렌더링 성능을 향상 시켜주는 Display List에 대해 알아보고자 한다. 사실 이 부분을 16장에 위치시키기에는 그 내용이 기본적이긴 하지만 필자 스스로의 혼란을 줄이기 위해 그냥 순서대로 번호를 매겼다. 이 강좌는 1장에 이여 두번째로 NeHe의 Display List를 그대로 번역한다. 이제 시작해 보자.  이 장에서는 OpenGL에서 공간상에 물체를 원하는 위치에 위치시키고 원하는 방향으로 움직이거나 회전하는 방법에 대해서 알아본다. 최종적 실습으로 두개의 구를 이용해서 첫번째 구는 화면 중앙에서 제자리에서 회전을 하며 두번째 구는 첫번째 구를 중심으로 일정한 거리를 유지하면서 동시에 자신의 중심점을 기준으로해서 회전하는 것을 구현해 본다. 좀더 다르게 표현한다면 첫번째 구는 자전만을 하며 두번째 구 역시 자전을 하면서 동시에 첫번째 구 주위를 공전하는 예를 말한다. OpenGL에서 이러한 일련은 동작은 간단한 수학적인 연산을 통해서 이루어진다고 강조하고 싶다. 물론 모든 컴퓨터의 동작의 모두가 수학적이기는 하지만 필자가 이 수학적이라는 것에 대해 강조하는 이유와 간단한 수학 연산이라고 말하는 이유는 다름 아닌 4X4 행렬, 이 하나만으로 모든 것이 이루어 진다는 것이다. Matrix(매트릭스)라는 영화를 보았는가? 매트릭스란 우리나라 말로 행렬이란 뜻이 있다. 즉, 공간상의 모든 원자, 요소들은 이 행렬을 통해서 통제되어질 수 있다. 고작 16개의 숫자들에 의해서 말이다. Matrix란 영화에서 인간들은 컴퓨터의 통제하에 움직이게 되는데 그 컴퓨터와 인간의 통제라는 내용과 Matrix란 영화의 제목이 그 어떤 강한 연관이 있다 느껴지지 않는가?
이 장에서는 OpenGL에서 공간상에 물체를 원하는 위치에 위치시키고 원하는 방향으로 움직이거나 회전하는 방법에 대해서 알아본다. 최종적 실습으로 두개의 구를 이용해서 첫번째 구는 화면 중앙에서 제자리에서 회전을 하며 두번째 구는 첫번째 구를 중심으로 일정한 거리를 유지하면서 동시에 자신의 중심점을 기준으로해서 회전하는 것을 구현해 본다. 좀더 다르게 표현한다면 첫번째 구는 자전만을 하며 두번째 구 역시 자전을 하면서 동시에 첫번째 구 주위를 공전하는 예를 말한다. OpenGL에서 이러한 일련은 동작은 간단한 수학적인 연산을 통해서 이루어진다고 강조하고 싶다. 물론 모든 컴퓨터의 동작의 모두가 수학적이기는 하지만 필자가 이 수학적이라는 것에 대해 강조하는 이유와 간단한 수학 연산이라고 말하는 이유는 다름 아닌 4X4 행렬, 이 하나만으로 모든 것이 이루어 진다는 것이다. Matrix(매트릭스)라는 영화를 보았는가? 매트릭스란 우리나라 말로 행렬이란 뜻이 있다. 즉, 공간상의 모든 원자, 요소들은 이 행렬을 통해서 통제되어질 수 있다. 고작 16개의 숫자들에 의해서 말이다. Matrix란 영화에서 인간들은 컴퓨터의 통제하에 움직이게 되는데 그 컴퓨터와 인간의 통제라는 내용과 Matrix란 영화의 제목이 그 어떤 강한 연관이 있다 느껴지지 않는가?  즉, 총 16개의 값을 가진 벡터 공간이다. 여기서 벡터 공간이라고 하는 것에 대해서 너무 신경 쓰지 말길 바란다. 그저 많은 벡터 공간중에 행렬도 포함된다는 정도만 알자. 자 이제 실제 행렬과 공간상의 좌표의 연산에 대해서 살펴보자.
즉, 총 16개의 값을 가진 벡터 공간이다. 여기서 벡터 공간이라고 하는 것에 대해서 너무 신경 쓰지 말길 바란다. 그저 많은 벡터 공간중에 행렬도 포함된다는 정도만 알자. 자 이제 실제 행렬과 공간상의 좌표의 연산에 대해서 살펴보자.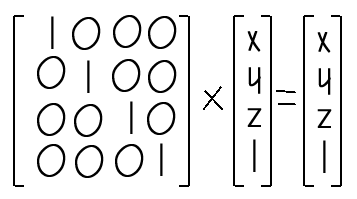 위 연산은 공간상의 임이의 점의 좌표 (x,y,z)가 크기가 4X4인 단위 행렬을 통해 아무런 위치의 변화없이 원래의 (x,y,z)의 위치값이 나오는 예이다. 주의해서 보면 위의 행렬 연산에서 좌측의 4X4 행렬이 단위 행렬임을 알수있다. 어떠한 행렬이건 단위행렬과 곱하면 본래의 행렬이 나온다는 것을 알고있는가? 그렇다면 이제 위의 행렬 연산에서 주어진 좌측의 4X4 행렬이 단위행렬이 아닌 다른 행렬일때 주어진 좌표는 어떤 새로운 좌표값으로 바뀔것이라는 것을 알수있다. 다행이 우리는 많은 선행대수학 교제에서나 컴퓨터 3차원 그래픽 서적에서나 좋은 OpenGL 서적에서 유용한 4X4행렬을 볼수있다. 첫째는 좌표를 원하는 위치로 이동할수있는 이동행렬, 둘째는 좌표를 원점(0,0,0)을 기준으로 회전시키는 회전행렬, 그리고 이밖에도 크기 변환 행렬(Scale Matrix), 밀림 행렬, 물체의 그림자를 얻어낼수 있는 그림자 변환 행렬 등등, 독자의 수학적 지식이 뛰어나면 뛰어날 수록 엄청나고 무궁 무진한 응용을 할 수 있겠다. 그렇다면 OpenGL에서 가장 많이 사용하고 있는 이동행렬, 회전행렬, 크기변환행렬 이렇게 세가지에 대해서 결과만을 알아보도록 하자.
위 연산은 공간상의 임이의 점의 좌표 (x,y,z)가 크기가 4X4인 단위 행렬을 통해 아무런 위치의 변화없이 원래의 (x,y,z)의 위치값이 나오는 예이다. 주의해서 보면 위의 행렬 연산에서 좌측의 4X4 행렬이 단위 행렬임을 알수있다. 어떠한 행렬이건 단위행렬과 곱하면 본래의 행렬이 나온다는 것을 알고있는가? 그렇다면 이제 위의 행렬 연산에서 주어진 좌측의 4X4 행렬이 단위행렬이 아닌 다른 행렬일때 주어진 좌표는 어떤 새로운 좌표값으로 바뀔것이라는 것을 알수있다. 다행이 우리는 많은 선행대수학 교제에서나 컴퓨터 3차원 그래픽 서적에서나 좋은 OpenGL 서적에서 유용한 4X4행렬을 볼수있다. 첫째는 좌표를 원하는 위치로 이동할수있는 이동행렬, 둘째는 좌표를 원점(0,0,0)을 기준으로 회전시키는 회전행렬, 그리고 이밖에도 크기 변환 행렬(Scale Matrix), 밀림 행렬, 물체의 그림자를 얻어낼수 있는 그림자 변환 행렬 등등, 독자의 수학적 지식이 뛰어나면 뛰어날 수록 엄청나고 무궁 무진한 응용을 할 수 있겠다. 그렇다면 OpenGL에서 가장 많이 사용하고 있는 이동행렬, 회전행렬, 크기변환행렬 이렇게 세가지에 대해서 결과만을 알아보도록 하자. 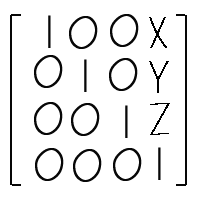 행렬의 원소중 X, Y, Z값은 각각 X축, Y축, Z축으로 그 값만큼 이동하고자 하는 값이다. 예를 들어서 공간상의 위치(3, 2, 4)를 X축으로 -1만큼, Y축으로 2만큼, Z축으로 1만큼 이동했을 경우에 대해서 알아보면 다음과 같을 것이다.
행렬의 원소중 X, Y, Z값은 각각 X축, Y축, Z축으로 그 값만큼 이동하고자 하는 값이다. 예를 들어서 공간상의 위치(3, 2, 4)를 X축으로 -1만큼, Y축으로 2만큼, Z축으로 1만큼 이동했을 경우에 대해서 알아보면 다음과 같을 것이다.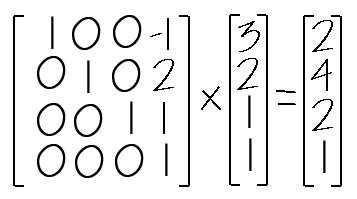 결과로써 (2,4,2)가 나왔는데 실제로 (3,2,1)을 위에서 언급한 이동을 하게 되면 (2,4,2)가 된다. 다음에 언급되는 모든 행렬의 사용법은 이와 동일하다.
결과로써 (2,4,2)가 나왔는데 실제로 (3,2,1)을 위에서 언급한 이동을 하게 되면 (2,4,2)가 된다. 다음에 언급되는 모든 행렬의 사용법은 이와 동일하다. 다음은 Y축을 기준으로 각 a만큼 회전시키는 회전 행렬이다.
다음은 Y축을 기준으로 각 a만큼 회전시키는 회전 행렬이다.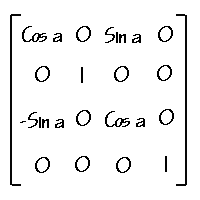 다음은 Z축을 기준으로 각 a만큼 회전시키는 회전행렬이다.
다음은 Z축을 기준으로 각 a만큼 회전시키는 회전행렬이다.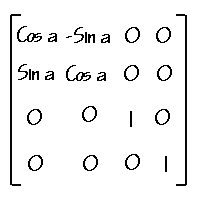 다음으로 알아 볼것은 은 크기 변환 행렬이다. 점은 크기를 갖지 않지만 점들이 모여서 물체를 이뤄 크기를 갖게 될때 유용한 변환 행렬이다. 원점을 기준으로해서 변환된다. 아래의 행렬이 바로 크기 변환 행렬이다.
다음으로 알아 볼것은 은 크기 변환 행렬이다. 점은 크기를 갖지 않지만 점들이 모여서 물체를 이뤄 크기를 갖게 될때 유용한 변환 행렬이다. 원점을 기준으로해서 변환된다. 아래의 행렬이 바로 크기 변환 행렬이다.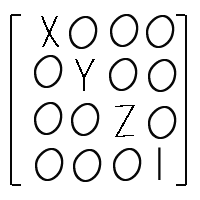 X값은 X축을 기준으로해서 X배의 크기로 변환되고 Y값은 Y축을 기준으로 해서 Y배의 크기로 변환되며 Z값은 Z축을 기준으로해서 Z배의 크리고 변환되게 된다.
X값은 X축을 기준으로해서 X배의 크기로 변환되고 Y값은 Y축을 기준으로 해서 Y배의 크기로 변환되며 Z값은 Z축을 기준으로해서 Z배의 크리고 변환되게 된다.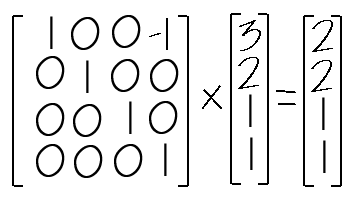 이동되어 (2,2,1)이라는 점으로 변환되었다. 다시 이점을 Z축으로 90도 회전시켜 변환되는 좌표는 다음과 같이 얻어질수있다.
이동되어 (2,2,1)이라는 점으로 변환되었다. 다시 이점을 Z축으로 90도 회전시켜 변환되는 좌표는 다음과 같이 얻어질수있다.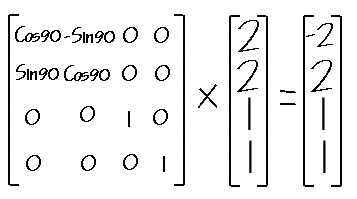 즉, 최종적으로 (-2, 2, 1)의 좌표가 얻어졌다. 원래의 좌표를 먼저 이동행렬 연산후에 다시 회전행렬 연산을 시켜 원하는 좌표를 얻은 것이다. 이것을 다음과 같이 계산할 수 있도 있음을 주의해서 보기바란다.
즉, 최종적으로 (-2, 2, 1)의 좌표가 얻어졌다. 원래의 좌표를 먼저 이동행렬 연산후에 다시 회전행렬 연산을 시켜 원하는 좌표를 얻은 것이다. 이것을 다음과 같이 계산할 수 있도 있음을 주의해서 보기바란다.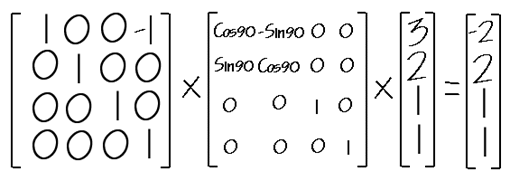 즉, 이동행렬과 회전행렬을 먼저 계산해서 얻어진 행렬에 변환하고자하는 좌표를 연산하여 최종적인 변환 좌표를 얻는 것이다. OpenGL은 이 방법을 사용한다. 이 예에서 우리는 이동행렬 연산후에 회전 행렬 연산을 수행했음을 눈여겨 봐야 한다. 그렇다면 순서를 바꿀경우 어떻게 될것인가? 즉 회전 행렬 연산후 이동 행렬 연산을 수행할 경우를 말이다. 직접 해보면 알겠지만 다른 결과 값이 나온다는 것을 알수있다.
즉, 이동행렬과 회전행렬을 먼저 계산해서 얻어진 행렬에 변환하고자하는 좌표를 연산하여 최종적인 변환 좌표를 얻는 것이다. OpenGL은 이 방법을 사용한다. 이 예에서 우리는 이동행렬 연산후에 회전 행렬 연산을 수행했음을 눈여겨 봐야 한다. 그렇다면 순서를 바꿀경우 어떻게 될것인가? 즉 회전 행렬 연산후 이동 행렬 연산을 수행할 경우를 말이다. 직접 해보면 알겠지만 다른 결과 값이 나온다는 것을 알수있다. 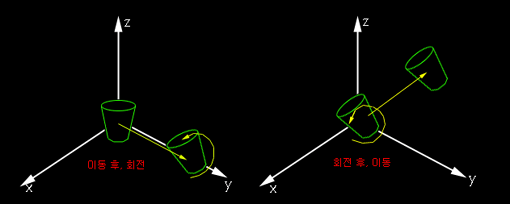 자, 이제 최종적으로 실제 예제를 통해서 이장을 마무리 지어 볼까 한다. 1장의 소스 코드에서 완전이 새롭게 시작하도록 하자.
자, 이제 최종적으로 실제 예제를 통해서 이장을 마무리 지어 볼까 한다. 1장의 소스 코드에서 완전이 새롭게 시작하도록 하자.