지도 객체가 map이라고 할때, 먼저 chart라는 이름의 그래픽 요소를 추가함.
map.layers().remove("chart");
let gl = new Xr.layers.GraphicLayer("chart");
map.layers().add(gl);
그래픽 요소가 표시되는 중심 좌표를 잡기 위해 참조되는 ShapeLayer가 ‘shpLyr’이라고 할때, 필요한 변수들을 준비함.
let graphicRows = gl.rowSet();
let lyr = map.layers("shpLyr");
let rows = lyr.shapeRowSet().rows();
let ars = lyr.attributeRowSet();
통계 데이터가 저장된 객체를 준비함. 이 객체는 네트워크를 통해 받은 데이터로 구성되는 것이 일반적임.
let tables = {
"description": "서울시 구별 코로나확진자 수 2020년 5월 18일 10시 기준",
"강남구": 71, "강동구": 19, "강북구": 8, "강천구": 31, "관악구": 53,
"광진구": 12, "구로구": 35, "금천구": 13, "노원구": 27, "도봉구": 14,
"동대문구": 34, "동작구": 37, "마포구": 24, "서대문구": 22, "서초구": 40,
"성동구": 22, "성북구": 27, "송파구": 44, "양천구": 23, "영등포구": 27,
"용산구": 34, "은평구": 30, "종로구": 18, "중구": 8, "중랑구": 17
};
이제 구성할 데이터의 수만큼 NailNumberGraphicRow 그래픽 요소와 1:1로 필요한 NailNumberShapeData를 생서하여 그래픽 레이어에 추가함.
for (var fid in rows) {
let aRow = ars.row(fid);
let sRow = rows[fid];
let pt = sRow.shapeData().representativePoint();
let title = aRow.valueAsString(0).trim();
let value = tables[title];
let nnsd = new Xr.data.NailNumberShapeData({
pos: [pt.x, pt.y],
outbox_size: [55, 55],
inbox_size: [42, 25],
title: title,
value: value,
title_offset_y: 1,
value_offset_y: 2
});
let nngr = new Xr.data.NailNumberGraphicRow(fid, nnsd);
graphicRows.add(nngr);
}
그래픽 요소들의 구성이 완료되면 실제 화면의 표시되도록 아래의 코드를 호출함.
gl.refresh();
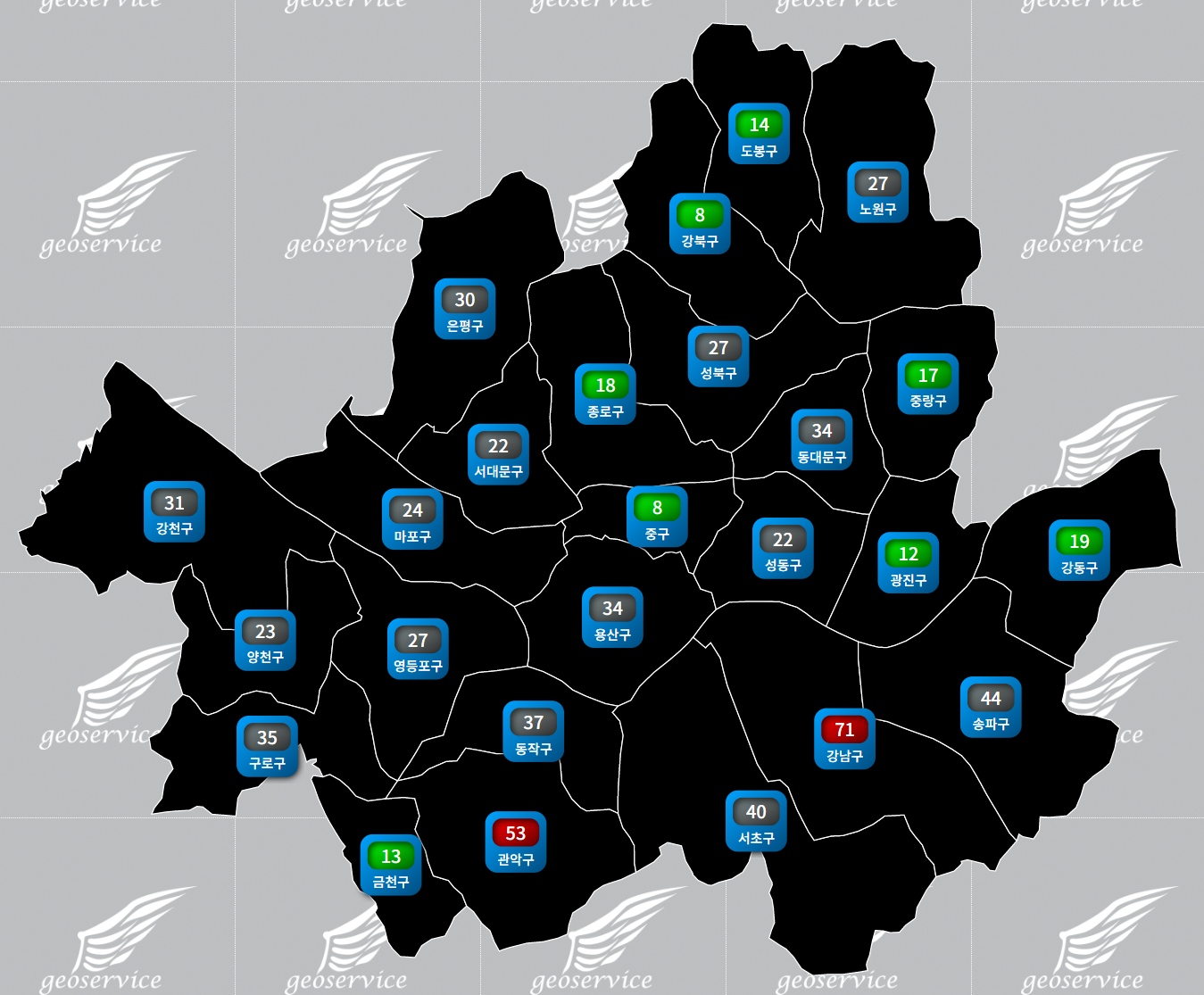
결과는 아래와 같음.
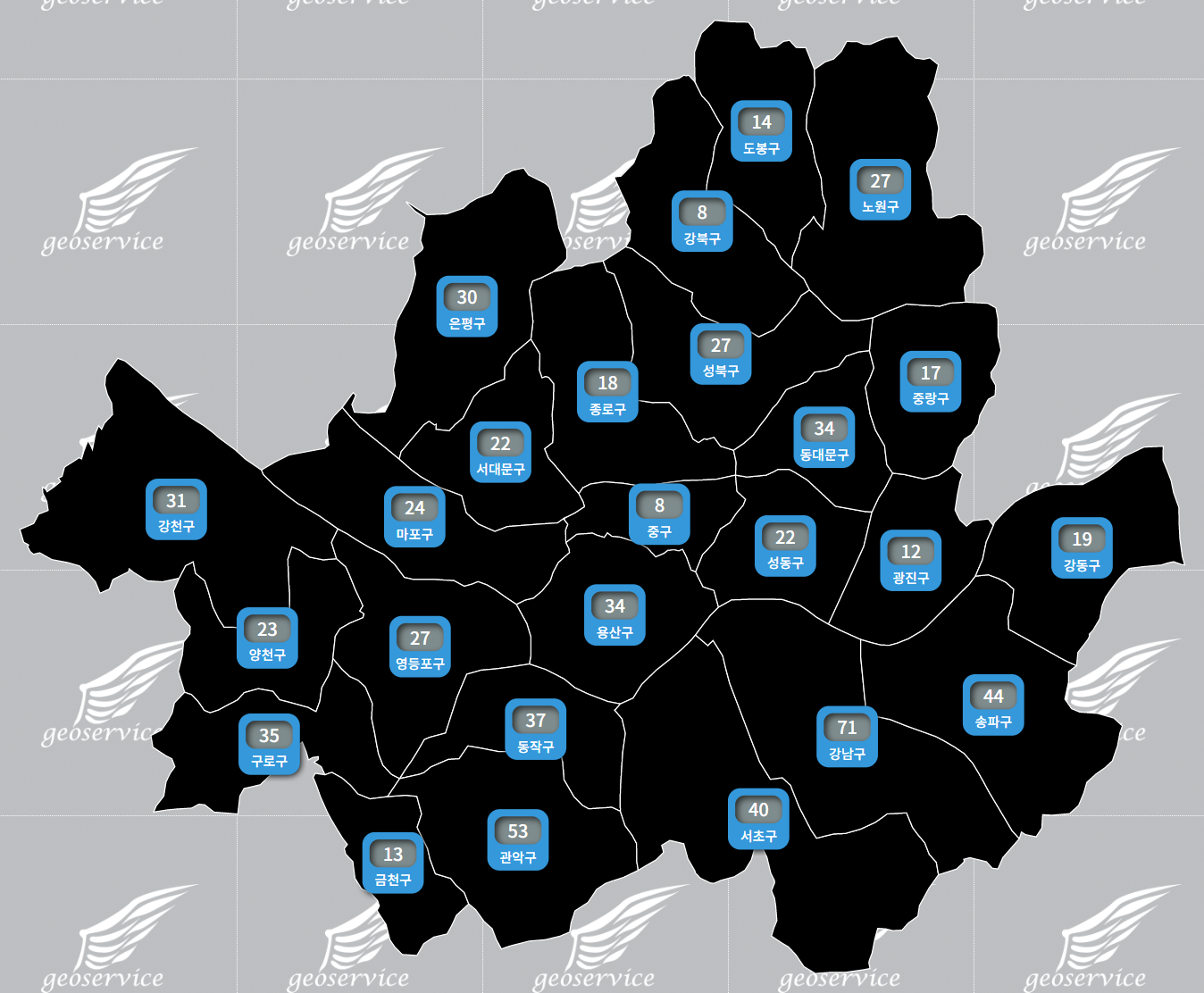
다소 밋밋한 표현인데, 이를 값에 따라 색상을 달리하고 색상을 단순 솔리드가 아닌 그라디언트 계열로 표현하기 위해 17번과 18번 코드 밑에 아래의 코드를 추가함.
nngr.brushSymbolForOutbox(new Xr.symbol.LinearGradientBrushSymbol());
if (value > 50) {
nngr.brushSymbolForInbox(new Xr.symbol.LinearGradientBrushSymbol({
stops: [
{ "offset": "0%", "step-color": "#ff0000" },
{ "offset": "100%", "step-color": "#660000" }
]
}));
} else if (value < 20) {
nngr.brushSymbolForInbox(new Xr.symbol.LinearGradientBrushSymbol({
stops: [
{ "offset": "0%", "step-color": "#00ff00" },
{ "offset": "100%", "step-color": "#006600" }
]
}));
} else {
nngr.brushSymbolForInbox(new Xr.symbol.LinearGradientBrushSymbol({
stops: [
{ "offset": "0%", "step-color": "#7F8C8D" },
{ "offset": "100%", "step-color": "#303030" }
]
}));
}
결과는 다음과 같음.