[GIS] Sutherland-Hodgman Polygon Clipping 알고리즘
하나의 매우 큰 폴리곤의 일부를 화면상에서 확대할 경우에 렌더링 속도가 매우 느려질 수 있습니다. 예를 들어 한반도 전역을 아우르는 큰 하천 수계를 하나의 폴리곤으로 구성되어 있을 경우에.. 이 폴리곤을 화면상에 모두 그려지도록 할 경우 렌더링 속도에는 큰 문제가 없으나 이를 점차적으로 확대해 갈수록 그리기 속도는 점점 더… 그리고 훨씬 느려지게 됩니다.
이런 현상을 막기 위한 가장 좋은 방법은 화면 밖으로 벗어나는 대부분의 폴리곤 영역을 날려 버리는 것입니다. 바로 이때 적용할 수 있는 효율적인 알고리즘이 Sutherland-Hodgman Polygon Clipping 알고리즘입니다.
아래의 그림을 살펴보면 사각형 영역의 폴리곤과 잘려나갈 폴리곤이 존재합니다. 사각형 영역의 폴리곤은 모니터 영역이라고 생각하면 이 알고리즘을 실제 지도 엔진단에 적용할 때 이해가 쉽겠습니다.
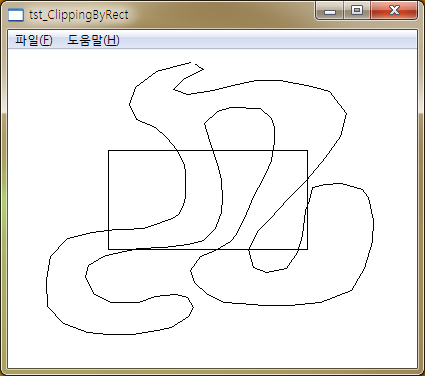
위의 상황에서 Sutherland-Hodgman Polygon Clipping을 적용한 결과는 아래와 같습니다.
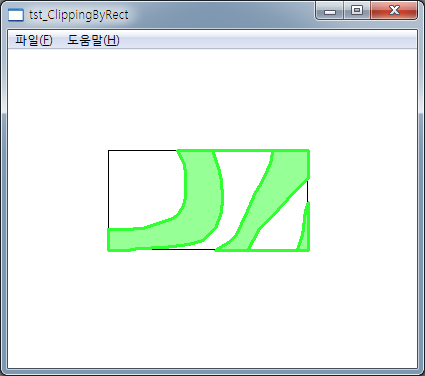
여기서 주의할 점은.. 이 알고리즘은 단지 폴리곤 렌더링에 적용할만하다 라는 점입니다. 이외의 부분에 대해서는 다른 알고리즘을 적용하기 바랍니다. 그 이유를 간단히 살펴보면 하나의 폴리곤을 화면 사각형에 대해 클리핑할때 다수의 폴리곤으로 분할되는 경우가 많은데 Sutherland-Hodgman Polygon Clipping 알고리즘은 다수의 폴리곤으로 분할하지 못하고 그 결과 역시 오직 하나의 폴리곤으로 클리핑하게 됩니다. 하지만… 그리기 위한 기능에서만큼은 그 어떠한 클리핑 알고리즘보다 빠른 퍼포먼스를 제공하므로 실제 적용할만한 알고리즘입니다.
이 알고리즘에 대한 소스 코드를 클래스화하여 제공합니다. 간단히 아래처럼 적용하면 원하는 결과를 얻을 수 있으리라 생각됩니다. 사용하는 좌표는 화면 좌표계입니다.
PolygonSHClipping clip; // 폴리곤 구성(시작점과 끝점은 같아야 함) clip.AddPoint(100, 100); clip.AddPoint(200, 100); clip.AddPoint(200, 200); clip.AddPoint(100, 200); clip.AddPoint(100, 100); // 클리핑 사각영역 지정 clip.SetClippingWindow(0, 0, 150, 150); // 클리핑 clip.Clip(); // 이후 클리핑된 영역을 그리기 위해서 다음 코드를 호출할 수 있다. clip.DrawOutput(hdc);
이 소스 코드의 활용과 위의 이미지에 대한 대한 데모에 대한 전체 코드는 아래를 통해 다운로드 받을 수 있습니다. 마우스 왼쪽 버튼으로 폴리곤을 구성하고 오른쪽 버튼을 누르면 클리핑된 폴리곤이 화면상에 표시됩니다.

