[Android] 맨날 까먹는 버튼 클릭 이벤트 핸들러 코드
맨날 까먹어 책 찾아 보고.. 인터넷 뒤져보고.. 해서 이 기회에 버튼에 대한 클릭 이벤트 핸들러 코드를 작성하는 것에 대해 정리를 해 놔야겠습니다. 머리가 나쁘니.. 손이 좀 고생을 해야겠지요..
레이아웃에 두개의 버튼이 있다고 가정하겠습니다. id는 각각 viewMode, editMode라고 하면.. 클릭 이벤트에 대한 핸들러 코드를 작성하는 방법에는 2가지가 있습니다. 물론 따져보면 둘다 동일한 방식이기는 하지만 코드 모냥새가 다르므로 다르다고 치겠습니다.
첫번째 방식입니다. 다수의 버튼들에 대한 이벤트 코드를 한자리에 가족같은 분위기로 다스리는 치국평천하 방식이라고 할 수 있겠습니다..
@Override
public void onCreate(Bundle savedInstanceState) {
findViewById(R.id.viewMode).setOnClickListener(btnClickListener);
findViewById(R.id.editMode).setOnClickListener(btnClickListener);
}
private Button.OnClickListener btnClickListener = new View.OnClickListener() {
@Override
public void onClick(View v) {
switch(v.getId()) {
case R.id.viewMode:
map.setMouseMode(MouseMode.MapViewMode);
break;
case R.id.editMode:
map.setMouseMode(MouseMode.EditMode);
break;
}
}
};
두번째 방식입니다. 이 방식은 각 버튼마다 이벤트 처리 코드를 따라 분리해 두는 방식입니다.
@Override
public void onCreate(Bundle savedInstanceState) {
....
findViewById(R.id.viewMode).setOnClickListener(
new Button.OnClickListener() {
@Override
public void onClick(View v) {
map.setMouseMode(MouseMode.MapViewMode);
}
}
);
findViewById(R.id.editMode).setOnClickListener(
new Button.OnClickListener() {
@Override
public void onClick(View v) {
map.setMouseMode(MouseMode.EditMode);
}
}
);
....
}
앞서도 말씀드렸지만.. 첫번째나 두번째나 결국 똑 같은 방식입니다..
세번째 방식은 상당히 직관적인 것으로 생각되는데요. 레이아웃을 정의하는 XML에서 터치 이벤트 함수명을 지정하고 간단히 소스코드에서 해당 이벤트 함수를 추가해 주기만 하면 됩니다. 예를 들어서 레이아웃을 정의하는 XML 중 버튼 부분만을 보면..
위의 버튼에 대한 터치 이벤트 함수인 onClickButton은 아래처럼, 해당 뷰를 사용하는 엑티비트의 구현부에 추가하면 됩니다.
public void onClickButton(View v) {
// 직관적이닷!
}
K-Means 알고리즘 구현
군집화 알고리즘(Clustering Algorithm) 중 K-Means 가 있습니다. K-Means 알고리즘에 대한 설명 이전에, 실제로 구현된 K-Means 알고리즘에 대한 실행 결과를 바로 설명하면서 자연스럽게 K-Means 알고리즘이 무엇인지 설명하겠습니다. 아래는 K-Means 알고리즘을 실행하기 위해 입력한 포인트 데이터입니다. SHP 파일을 통해 입력 받았습니다.

위의 이미지처럼 공간상에 무수히, 주관적 해석이긴 하지만 의미 없이 분포되어 있는 포인트들에 대해서 어떤 연관 관계에 대한 특성을 부여함으로써 몇개로 묶을 수 있는데요. 이처럼 묶는다라는 것을 그룹핑, 클러스터링이라고 합니다. K-Means 알고리즘에서 몇개(K개)로 묶을지를 지정하여 원하는 개수 만큼 클러스터링할 수 있습니다. 아래의 화면은 K-Means 알고리즘을 활용하여 12개의 그룹으로 공간상의 포인트를 묶은 결과입니다.
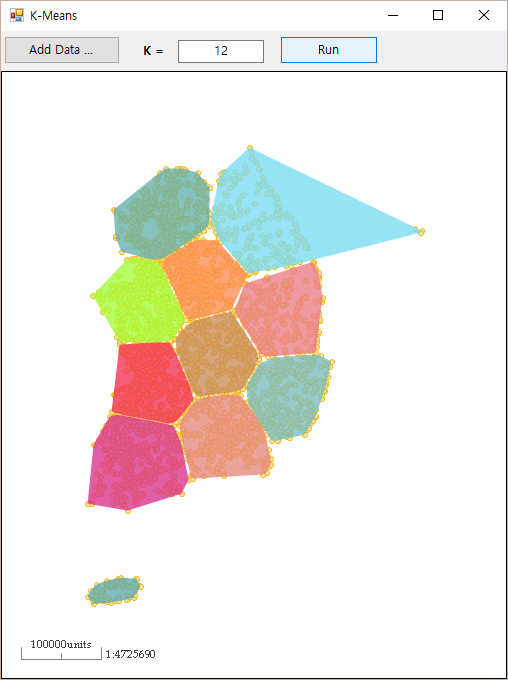
앞서 포인트를 그룹으로 묶을 때 어떤 관계에 대한 특성을 부여한다고 하였는데요. 위의 화면에서는 그 특성을 거리(Distance)로 하였습니다. 즉, 거리 상으로 가까운 포인트들을 그룹으로 묶는 것입니다.
이처럼 이미 확보한 수 많은 공간상의 데이터를 그룹핑하여 놓는다면, 새로운 포인트에 대해서 어느 그룹에 포함되는지에 대한 해석이 매우 빠르게 분류될 수 있습니다. 이미 확보한 데이터가 많으면 많을 수록, 새로운 데이터에 대한 해석이 보다 더 정확할 수 있겠죠.
아래는 K-Means 알고리즘을 구현한 C# 소스코드이며, 듀라맵(DuraMap-Xr)을 이용하여 K-Means 알고리즘에 필요한 포인트 데이터를 SHP 파일로부터 읽어 들이고 그 결과를 시각화 하였습니다.
Convex-Hull 알고리즘 구현
Convex Hull은 볼록한 껍데기로.. 무수히 많은 포인트를 감싸는 볼록한 영역으로 정의할 수 있습니다. 입력 데이터인 포인트는 SHP 파일로부터 제공받아, 이를 듀라맵에서 그 결과를 표시하도록 하였습니다. 아래는 그 결과 화면입니다.
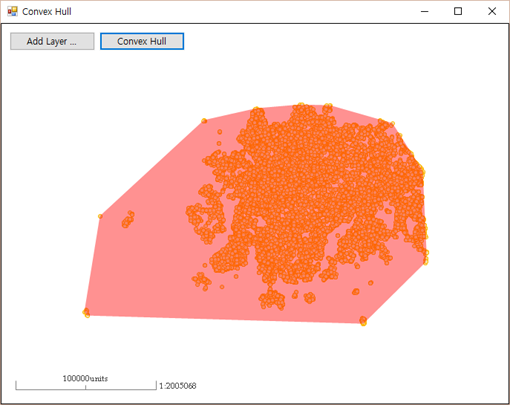
무수히 많은 작은 포인트를 감싸는 Convex Hull이 반투명한 빨간색 폴리곤으로 표시되어져 있습니다. 이러한 Convex-Hull에 대한 구현에 대해 C# 클래스로 정의했으며 아래와 같습니다.
using System;
using System.Collections.Generic;
namespace tstConvexHull
{
public class ConvexHull
{
public class Point : IComparer
{
public double x;
public double y;
public Point()
{
x = 0.0;
y = 0.0;
}
public Point(double x, double y)
{
this.x = x;
this.y = y;
}
public int Compare(Point p1, Point p2)
{
if (p1.x == p2.x)
{
return p1.y > p2.y ? 1 : p1.y < p2.y ? -1 : 0;
}
else
{
return p1.x > p2.x ? 1 : p1.x < p2.x ? -1 : 0;
}
}
}
public static double Cross(Point O, Point A, Point B)
{
return (A.x - O.x) * (B.y - O.y) - (A.y - O.y) * (B.x - O.x);
}
public static Point[] Get(Point[] P)
{
if (P.Length > 1)
{
int n = P.Length, k = 0;
Point[] H = new Point[2 * n];
Array.Sort(P, new Point());
for (int i = 0; i < n; ++i)
{
while (k >= 2 && Cross(H[k - 2], H[k - 1], P[i]) <= 0)
k--;
H[k++] = P[i];
}
for (int i = n - 2, t = k + 1; i >= 0; i--)
{
while (k >= t && Cross(H[k - 2], H[k - 1], P[i]) <= 0)
k--;
H[k++] = P[i];
}
if (k > 1)
{
Point[] NewH = new Point[k - 1];
Array.Copy(H, NewH, k - 1);
H = NewH;
}
return H;
}
else if (P.Length <= 1)
{
return P;
}
else
{
return null;
}
}
}
}
실제 위의 Convex-Hull 클래스에 대한 사용은 아래 코드와 같은데요. DuraMap-Xr에서 SHP 파일로부터 점 데이터를 읽어 입력 데이터를 구성하여 Convex-Hull을 실행하고 그 결과로 반투명 빨간색 폴리곤을 추가하는 코드 모두를 나타내고 있습니다.
XrMapLib.ShapeMapLayer lyr = axXr.Layers.GetLayerAsShapeMap("lyr");
XrMapLib.ShapeTable tbl = lyr.ShapeTable;
int cntRows = tbl.RowCount;
ConvexHull.Point[] pts = new ConvexHull.Point[cntRows];
for(int i=0; i
코드를 살짝 설명하면, 1~15번 코드는 SHP 파일로부터 포인트 데이터를 읽어와 Convex-Hull 알고리즘에 입력할 데이터를 준비하는 것이고, 17번 코드가 바로 Convex-Hull의 실행이며 19번 코드부터는 Convex-Hull의 결과를 그래픽 객체로 가시화시켜주는 코드들입니다.
크로스 도메인(Cross Domain)을 허용하는 OpenAPI 개발을 위한 JSONP
AJAX 방식은 서로 다른 도메인간의 데이터를 받아 오는 것을 기본적으로 막고 있지만, JSONP라는 방법을 이용해 가능하게 됩니다. 이에 대해 정리해 봅니다. JSONP 방식의 OpenAPI를 제공하는 Java 서블릿 중 doGet 함수는 다음과 같습니다.
protected void doGet(HttpServletRequest request, HttpServletResponse response)
throws IOException
{
String name = request.getParameter("name");
String nameDecoded = URLDecoder.decode(name, "UTF-8");
String callbackFunction = request.getParameter("callback");
String responseData = "({\"Value\": \"Hello, " + nameDecoded + "\"})";
String result = callbackFunction + "("+ responseData + ");";
response.setContentType("application/json;charset=UTF-8");
response.setCharacterEncoding("UTF-8");
response.setStatus(HttpServletResponse.SC_OK);
response.setContentType("text/javascript");
PrintWriter out = response.getWriter();
out.println(result);
}
위의 OpenAPI는 클라이언트 측에서 name과 callback이라는 파라메터를 전달해 준다라는 전제 조건을 갖습니다. 서버는 자신에게 전달된 name을 이용해 클라이언트에게 다시 Hello로 구성된 문자열을 결과로 전달해 줍니다. 여기서 전달 방식이 중요한데요. 그 전달방식이 바로 JavaScript 함수호출에 대한 코드입니다. 이 코드 문자열을 클라이언트가 받아 실행해 준다라는 것입니다. 실제로 위의 서블릿에 대해 웹 브러우저를 통해 호출해 보면 다음과 같습니다.
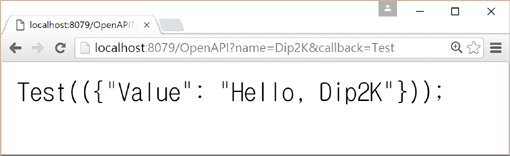
위의 URL 호출을 좀더 설명하면, name 파라메터에는 Dip2K를 지정했고, callback 파라메터에는 Test를 지정했습니다. 그 호출 결과는 Value를 키로 하고 Hello, Dip2K를 값으로 하는 객체를 인자로한 Test 함수의 호출 코드에 대한 문자열입니다. 클라이언트에서 이 문자열을 코드화하여 실행해주면 성공적으로 서버에서 전달한 데이터를 받아 처리할 수 있게 되는 것입니다.
실제로 아래의 코드는 jQuery를 이용해 JSONP 방식으로 크로스도메인 문제를 깔끔하게 해결해 데이터를 주고 받는 코드입니다.
var url = 'http://www.gisdeveloper.co.kr:8079/OpenAPI?name=김형준&callback=?';
$.ajax({
url: url,
type: 'get',
dataType: 'jsonp',
success: function (data) {
alert(data.Value);
}
});
실행 결과는 ‘Hello, 김형준’을 표시하는 Alert 창 입니다.

