플랙스에서 컴포넌트의 스킨을 디자인하는 가장 쉬운 방법은 이미지를 이용하는 것입니다. 예를 들어 버튼의 경우.. 버튼의 up, over, down, disabled 상태에 따라 각기 다른 이미지를 만들어 주고 지정해 주면 됩니다. 디자이너의 역량에 따라 매우 높은 퀄리티를 낼 수 있습니다.
이 글은 이미지를 이용하는 방식이 아닌.. 각 상태에 따라 직접 그려주는 방법에 대한 설명입니다. 이렇게 이미지가 아닌 직접 버튼의 스킨을 그려주는 방식에 대한 장점은… 버튼의 크기가 변경이 되어도 스킨이 깨지않고 자연스럽게 표현할 수 있다는 점입니다.
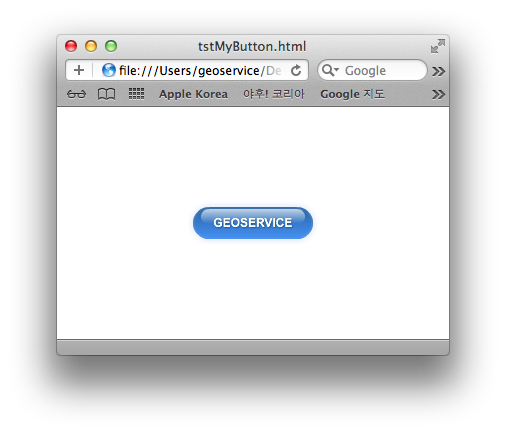 설명을 위해 제가 테스트 해 본 것은 버튼을 Aqua Style로 표현해 보는 것입니다. 위의 이미지가 실제 제 스스로 만들어본 버튼에 대한 Aqua 스킨입니다. SparkSkin 클래스의 파생 중에서 버튼에 대한 스킨은 SparkButtonSkin입니다.
설명을 위해 제가 테스트 해 본 것은 버튼을 Aqua Style로 표현해 보는 것입니다. 위의 이미지가 실제 제 스스로 만들어본 버튼에 대한 Aqua 스킨입니다. SparkSkin 클래스의 파생 중에서 버튼에 대한 스킨은 SparkButtonSkin입니다.
일반적으로 SparkSkin은 레이어라는 개념으로 스킨을 입히게 됩니다. 여기서 직접 만들어 볼 버튼의 Aqua Style은 다음과 같은 레이어로 구성되어져 있으며 위의 이미지에 대한 버튼이 바로 아래의 레이어로 구성되어져 있습니다.
- border
- aqua
- labelDisplay
- blaze
좀더 고급스러운 Aqua 스타일을 제공하기 위해서는 더 많은 레이어가 필요하겠지만.. 간단이 이 정도의 레이어만을 구성해 봄으로써 Aqua 스타일의 스킨을 버튼에 입혀 보겠습니다. 위의 레이어 중 labelDisplay는 반드시 존재해야 하는 id 명으로써 버튼의 텍스트 라벨이 적용될 것으로 실제 Label 컴포넌트로 구성됩니다. 또한 위의 4개의 레이어의 순서 역시 중요합니다. 즉 가장 밑에 border가 존재하고 그 위에 aqua가.. 그리고 labelDisplay가 위치하며 가장 위에 blaze가 나타납니다.
먼저 실제 border 에 대한 FXG 코드입니다. 플렉스는 스킨에 대해 FXG(Flash XML Graphic)를 이용해 그려줍니다.
위의 FXG 코드는 다음과 같은 결과를 그려냅니다.

다음은 aqua 에 대한 FXG입니다.
위의 FXG 코드에 대한 결과는 다음과 같습니다.

그리고 라벨 텍스트를 표현할 코드는 다음과 같습니다.
텍스트를 표현해기 위해 Label 컴포넌트를 사용했습니다. 결과는 다음과 같습니다.

끝으로 blaze 레이어에 대한 FXG 코드는 다음과 같습니다.
이 레이어 만을 하얀색 배경의 화면상에서 보면 보이지 않는데요. 이 레이어는 버튼 위에 광택 효과를 주는 것으로 Aqua 버튼의 최정 결과를 보시면 딱! 아실 겁니다. ^^
뭐… 글로 아무리 길게 장황하게 써도.. 해당 스킨에 대한 전체 코드를 다음 url을 통해 다운로드 받으실 수 있으니 실제 플렉스에서 적용해 보시기 바랍니다.

참고로.. SparkSkin을 통한 스킨 적용은 Flash Builder 4.0 이상에서만 적용된다는 점에 유의하시기 바랍니다. 최근 4.6까지 나왔지요? 저는 4.5 버전을 쓰고 있습니다만…. 여튼.. 위의 스킨을 실제 버튼에 적용하기 위한 방법은 3가지가 있는데.. 그 중에 한가지에 대한 코드는 다음과 같습니다.
스킨을 만드는 작업은.. 코드의 길이에 비해 상당히 많은 시간이 소요되는 작업이라고 생각합니다. 또한 제대로 스킨을 만들려면 디자인 감각까지 갖춰야 하는 매우 고난위도의 작업입니다. 하지만 일단 한번만 만들어 놓으면 지속적으로 활용할 수 있으니… 스킨 제작 작업은 시간과 비용이 소요되더라도 꼭 제대로 해두는 것이 최종 프로젝트 산출물의 가치를 배가 시킬 수 있을 거라 확신합니다.


 설명을 위해 제가 테스트 해 본 것은 버튼을 Aqua Style로 표현해 보는 것입니다. 위의 이미지가 실제 제 스스로 만들어본 버튼에 대한 Aqua 스킨입니다. SparkSkin 클래스의 파생 중에서 버튼에 대한 스킨은 SparkButtonSkin입니다.
설명을 위해 제가 테스트 해 본 것은 버튼을 Aqua Style로 표현해 보는 것입니다. 위의 이미지가 실제 제 스스로 만들어본 버튼에 대한 Aqua 스킨입니다. SparkSkin 클래스의 파생 중에서 버튼에 대한 스킨은 SparkButtonSkin입니다.