디자인은 죽었는가?
Is Design Dead?
Martin Fowler
Chief Scientist, ThoughtWorks
이 자료는 2004년 5월의 문서를 참고로 작성되었습니다. Last Significant Update: May 2004
익스트림 프로그래밍(Extreame Programming, 이하 XP)을 여기저기서 일시적으로 접해보면, XP가 소프트웨어 디자인의 종말을 부르는 것 같다. 많은 디자인 활동이 “Big Up Front Design”이라 하여 조롱거리가 되고, UML이나 유연한 프레임워크, 또한 패턴들까지도 중요하지 않다거나 노골적으로 무시되고 있다. 사실 XP는 무수히 많은 디자인을 필요로 하지만, 기존의 소프트웨서 프로세스들과는 다른 방식으로 다룬다. XP는 실천들(practices)을 통한 진화적인 디자인이란 개념으로 다시 새로워지고(rejuvenated) 있다. 이 실천이란 진화가 곧 가시적인 디자인 전략이 되는 것이다. XP는 또한 디자이너로서 배워야할 기술에 대한 도전이 생기게 한다. 어떻게 간단(simple)하게 디자인 할것인가, 디자인을 깔끔하게 유지하기 위해 리팩토링(refactoring)을 어떻게 사용해야 하나, 진화적인 스타일로 개발을 할때 패턴들을 어떻게 사용해야 하나, 등의 도전을 받게 되는 것이다.
익스트림 프로그래밍(XP)는 소프트웨어 개발에 관련된 많은 일반적인 가정들에 도전하고 있다. 이것들중 가장 큰 논쟁거리가 되는 것은 우선적(up-front) 디자인에 상당한 노력을 기울이는 것을 거부하고, 좀더 진화적인 접근을 지지하는 데 있다. XP의 비방자들에게 이것은 – 대개 해킹으로 치부되는 – “짜보고 고치기(code and fix)’ 개발방식으로의 회귀이고, 지지자들에게 이것은 UML같은 디자인 테크닉이나 원칙, 패턴들에 대한 거부로 받아들여진다. 디자인에 대해선 염려말라, 만약 당신이 당신의 코드에 귀울이고 집중한다면 좋은 디자인이 나타날것이다.
내 자신은 이러한 논쟁의 중심에 있다. 나의 대부분의 경력은 그래픽한 디자인 언어 – UML과 그것의 선구자들 -와 패턴들에 관련되어 있다. 사실 UML과 패턴에 관한 책들도 썼다. 그렇다면 내가 XP 를 받아들인다는 것이 내가 이러한 주제들로 써온 책들을 모두 부인하고, 기존의 보수적인 개념들을 깨끗이 지웠다는 얘기인가?
자~ 나는 이런 드라마틱한 긴장감의 울타리속에 당신을 가둬놓을 생각은 없다. 간단한 대답은 ‘아니다’이다. 길게 얘기하자면 이 문서의 나머지 부분이 해답이다.
계획된 디자인과 진화적 디자인 – Planned and Evolutionary Design
나는 이 문서를 통해 디자인이 어떻게 완성되는지에 관한 두가지의 소프트웨어 개발 스타일을 설명할 것이다. 아마 대부분은 진화적인 디자인일 것이다. 본질적으로 진화적 디자인이란 시스템이 구현됨에 따라 시스템의 디자인이 성장하는 것이다. 디자인은 프로그래밍 프로세스의 일부분이고 프로그램이 진전됨에 따라 디자인은 변한다.
일반적인 사용예에서는 진화적인 디자인은 재앙이다. 그 디자인은 코드를 변경하기 더욱 어렵게 만드는, 그때그때의 임기응변식 결정 덩어리의 집합으로 마무리 된다. 여러가지 방식으로 이것은 디자인이 아니다라는 논의도 가능하다.분명히 이것은 대개 바보같은 디자인이 된다. Kent 가 표현하듯이, 디자인은 오랜 기간동안 소트웨어를 쉽게 변경할 수 있도록 유지하기 위해 존재한다. 디자인의 질이 떨어질수록, 변경을 효율적으로 할수 있는 당신의 능력도 떨어진다. 당신은 시간이 지남에 따라 디자인이 더욱더 나빠지는, 소프트웨어 엔트로피(entropy)의 상태에 있는 것이다. 소프트웨어를 변경하기 어렵게 만드는것 뿐 아니라, 버그가 찾기 어렵고 안전하게 제거하기 어려울뿐아니라 더욱 널리 퍼지기 쉽게 만드는 것이다. 이것은 프로젝트가 진행됨에 따라 버그를 고치는 비용이 급격하게 증가하는, “짜보고 고치기”의 악몽이다
계획된 디자인은 이것과 반대이며, 공학의 다른 분야에서 나온 개념을 내포하고 있다. 당신이 개집을 지으려고 한다면, 그냥 나뭇가지를 대충 엮어서 조잡한 모양으로 지으면 된다. 그러나 초고층 빌딩을 짓는다면, 이러한 방식으로 지을수 없다 – 미처 반도 짓기 전에 무너질 것이기 때문이다. 그래서 당신은, 내 아내가 Boston 에서 일하는 곳과 같은 건축설계 사무소에서 그려진, 건축 도면으로부터 시작한다. 그녀는 디자인을 해 나가면서, 일부 수학적인 분석이 필요한 것과, 대부분은 건축 규약과 관련된 모든 핵심들을 알아나간다. 건축 규약은 (약간의 수학을 밑바탕으로 하는) 작업 경험을 기초로 건축물을 어떻게 디자인할 것인가에 관한 규칙이다. 일단 디자인이 완성되면, 내 아내의 건축공학 사무소는 건물을 짓는 다른 회사에 디자인을 넘길수 있게 된다.
계획된 디자인은 소프트웨어에서도 똑같은 방식이다. 디자이너(설계자)들는 사전에 모든 큰 핵심들에 대해 깊이 생각한다. 그들은 소프트웨어를 구축하는 것이 아니라 디자인 하는 것이기 때문에 코드를 작성할 필요가 없다. 그래서 그들은 UML과 같은 – 약간의 프로그래밍에 세부적인 항목으로 부터 떨어져서, 좀더 추상적인 단계에서 작업할 수 있는 – 디자인 테크닉을 사용한다. 디자인이 완성되면 다른 부서(또는 다른 회사)에 디자인을 넘기면 된다. 디자이너들은 굉장히 큰 규모를 생각하기 때문에, 소프트웨어 엔트로피를 증가시키는 심각한 임시응변의 결정을 피할 수가 있다. 프로그래머들이 디자인을 받아들인다면, 디자인 방향을 따라서 훌륭한 시스템을 구축할 수 있다.
계획된 디자인 기법은 70년대부터 있었고, 많은 사람들이 사용해 왔다. 여러가지 면에서 ‘짜보고 고치기’의 진화적 디자인보다 나은 점도 있다. 그러나 몇가지 결함이 있는데, 그 첫째가 프로그래밍할때 다루어져야할 핵심들의 모든 부분을 생각한다는 것이 불가능하다는 것이다. 그래서 프로그래밍할때 디자인에 의문을 제기할 일이 꼭 생긴다는 것이다. 그러나 디자이너는 일을 마쳤고, 다른 프로젝트에 이동한 상황이라면 어떻게 될 것인가? 프로그래머는 디자인에 따라 코딩을 시작하였고 엔트로피는 이미 시작되었다. 디자이너가 옆에서 도와 주는 상황이라도, 디자인 문제들을 가려내고, 도면을 바꾸는 것은 시간이 걸리는 작업이고, 또한 코드도 다시 변경해야 한다. 그리고 거기에는 언제나 시간 압박과 빨리 고쳐야 한다는 강박관념도 존재한다. 따라서 엔트로피는 또 다시 증가하게 된다.
게다가 문화적인/실력적인 문제도 종종 나타난다. 디자이너는 기술과 경험을 통해 디자이너가 되는 것인데, 그들은 디자인하기에 너무 바빠서 코딩할 틈이 없다. 그러나 도구나 소프트웨어 개발 자료들은 급격하게 변해간다. 당신이 더 이상 코딩을 하지 않는다면 이러한 기술 흐름의 변화를 놓칠 뿐만 아니라, 또한 코딩하는 사람들에게 존경받지도 못할 것이다.
구축자(건축시공자)와 디자이너(건축설계자)와의 긴장관계는 건축분야에서도 나타나지만, 소프트에어 쪽이 더욱 심하다. 건축과 소프트웨어는 중요한 차이가 있기 때문이다. 건축에서는 시공자와 디자이너의 기술에 명확한 차이가 있지만 소프트웨어는 그렇지가 않다. 디자인을 중요시하는 환경에서 일하는 프로그래머라면 분명 오랜경험과 숙련을 필요로 한다. 특히나 디자이너가 날마다 변해가는 개발 플랫폼에 대한 지식이 부족하다면, 디자이너가 설계한 디자인에 대해 프로그래머 문제점을 제기할수 있을 정도로 숙련되어야 한다.
오늘날 이러한 문제들은 해결이 가능하다. 인간적인 긴장관계를 처리함으로 해결할 수 있다. 또는 대부분의 문제점을 다룰수 있는 능력있는 디자이너를 구하거나 도면변경이 가능하도록 잘 충분히 숙달된 프로세스를 가지고서 해결할 수도 있다. 그러나 여전히 다른 문제가 있다. 바로 “요구사항 변경”이다. 요구사항 변경이야말로 내가 내가 참여한 소프트웨어 프로젝트에서 최고로 머리 아픈 골칫거리이다.
요구사항 변경을 다루는 한 방법은 디자인을 유연하게 함으로서 요구가 변함에 따라 쉽게 변할수 있게 하는것이다. 그러나 이 방법은 어떤 것이 변할것인가를 아는 통찰력이 필요하다. 디자인이 변덕스런 영역들을 다룰수 있도록 계획될수는 있다. 그러나 이것이 예견된 요구사항 변경에는 도움이 되지만, 예견되지 않은 변경에 관해선 도와주지 못한다 (오히려 나쁜영향을 미친다). 그래서 변덕스런 영역들을 분리해 낼수 있도록 요구사항들을 확실히 이해해야 한다. 내 경험으론 이것은 매우 어렵다.
이러한 요구사항과 관련된 문제점의 일부는 요구사항을 충분히 이해하지 못하기 때문이다. 그래서 많은 사람들이 디자인이 나중에 변경되지 못하게 할거란 희망으로, 미리 필요한 요구사항을 잘 뽑아내 주는 요구 공학 프로세스에 초점을 맞추고 있다. 그러나 이러한 방향도 해결책이 되지 못한다. 많은 예견되지 않은 요구사항 변경은 비지니의 변경에 의해서 발생한다. 아무리 요구공학 프로세스를 신중히 하더라도, 이것들은 대비할 수는 없다.
이런 모든 것이, 계획된 디자인이 불가능한것처럼 들리게 만든다. 분명 이것들은 큰 문제이다. 그러나 나는 대개 일반적으로 “짜보고 고치기”식으로 사용되는 진화적인 디자인에 비해 계획된 디자인이 더 나쁘다는 주장을 할 생각은 없다. 실제로 난 “짜보고 고치기”보다 계획된 디자인을 좋아한다. 그치만 난 계획된 디자인의 문제점도 알고 있기 때문에 새로운 방향을 찾고 있는 것이다.
XP를 가능하게 하는 실천들 – The Enabling Practices of XP
XP 는 여러가지면에서 논쟁거리가 되고 있다. 그중 가장중요한 것은 XP가 계획된 디자인이 아닌 진화적 디자인을 지지한다는 것이다. 알다시피, 진화적 디자인은 그때그때의 디자인 결정과 소프트웨어 엔트로피 때문에 제대로 수행되지 못는다.
위의 논쟁을 이해하는데에 있어 핵심이 되는 것은 소프트웨어 변경 곡선이다. 변경 곡선이란, 프로젝트가 진행될수록 변경에 드는 비용이 지수적으로 더욱 증가한다는 것이다. 변경 곡선은 일반적으로 “분석단계에서 1달러인 변경 비용이 생산단계에서는 1000달러가 든다”라는 개념으로 표현된다. 아이러니하게도 분석단계가 없는 임시방편적인 프로세스 속에서도 대부분의 프로젝트가 여전히 수행된다. 하지만 지수증가의 법칙은 여기에도 역시 존재한다. 지수증가적인 변경곡선은 진화적인 디자인이 실현 불가능하다는 것을 의미한다. 이는 또한 계획된 디자인이 매우 주의 깊에 이루어져야 한다는 것을 뜻하는데, 왜냐하면 계획된 디자인에서의 실수도 또한 진화적 디자인과 같은 지수증가의 법칙을 따르기 때문이다.
XP의 근본이 되는 기본적인 전제는 진화적인 디자인이 제대로 수행될 수 있도록 변경곡선을 완만하게 할 수 있다는 것이다. 이렇게 완만하게 하는 것은 XP에 의해서 ‘가능’해지고, 또한 이 완만함을 XP가 ‘사용’한다. 이것이 XP 실천들이 서로 연결된 부분인데, 말하자면 이렇게 완만함을 ‘가능’케 하게 하는 실천들이 없이는 완만하게 된 곡선을 ‘사용’하는 XP의 요소를 실천할수 없다. XP에 대한 논쟁이 대부분 여기서 생긴다. 많은 사람들이 ‘가능’케 하는 것에 대한 이해 없이 ‘사용’하는 부분을 비판 한다. 대개 이러한 비판은 비판가들 자신의 경험으로 부터 오는데, 그들은 실천이 제대로 ‘사용’되게 하는 ‘가능’케 하는 실천들을 해보지 않았다. 결국 그들은 한번 데었었기 때문에 XP를 만나게 되면 그 아팠던 기억이 나게 되는 것이다.
가능케 하는 실천에는 많은 부분들이 있다. 핵심은 테스팅과 지속적 통합의 실천이다. 테스팅을 통한 안정성 없이는 XP의 나머지 부분들은 불가능하다. 지속적 통합은 팀을 동기화 시키기 위해 필요하고, 이로 인해 다른 사람과 통합하는 것에 대해 걱정할 필요없이 변경을 할 수 있다. 이 두 실천은 변경 곡선에 큰 영향을 준다. 난 이것을 ThoughtWorks 회사에서 다시 한번 느꼈다. 테스팅과 지속적 통합을 도입함으로 개발 성과에 눈에 띄는 향상을 가져왔다. 거대한 향상을 얻고자 한다면 모든 실천들이 필요하다는 XP의 주장에 대해 확실히 연구해 볼만하다.
리팩토링도 비슷한 영향력을 가진다. XP가 제안한 훈련방식대로 코드를 리팩토링하는 사람이라면 제멋대로 하는 것과는 다른 확실한 차이를 느낄것이다. 이것은 Kent가 나에게 제대로 리팩토링하는 것을 가르쳐 주었을때의 나의 경험이다. 결국, 이런 강렬한 느낌/변화만이 그것에 관한 책을 쓸만한 동기를 줄수 있었을 것이다..
Jim Highsmith는 그의 훌륭한 글인 “XP의 요약” 에서, 천칭으로 예들 들었다. 한쪽 편의 접시는 계획된 설계를 놓고, 반대쪽에는 리팩토링을 놓는다. 예전까지의 접근법에서는 계획된 디자인쪽으로 천징이 기울고 있는데, 이는 나중에 변경을 가할수 없다는 전제가 있기 때문이다. 변경에 드는 비용이 낮아짐에 따라 추후에 리팩토링으로 디자인에 더 많은 일을 할수 있게 되었다. 계획된 디자인이 완전이 사라지지는 않겠지만, 현재 두가지 디자인 방식을 제대로 함께 적용할수 있는 균형이 맞춰졌다. 내가 느끼기에, 리팩토링 이전에는 마치 한손으로 모든 디자인을 했던것 같다.
XP를 가능케하는 지속적인 통합, 테스팅, 리팩토링 실천들은, 진화적인 디자인이 그럴듯해 보이게하는 새로운 환경을 제공한다. 그러나 우리가 아직 이해하지 못한것은 균형점이 어디냐는 것이다.
눈에 보이는 감동적인 것에도 불구하고, XP는 단순히 테스트, 코딩, 리팩토링이 아닌것이 확실하다. 코딩 이전에 디자인할 가능성이 있다. 이중 조금은 코딩이 전혀 하지 않은 때이고, 대부분은 특정 영역을 코딩하는 반복작업속에서 나타난다. 그러나 여기에는 우선적디자인(up-front)과 리팩토링 사이에 또다른 균형이 있다.
‘단순함’의 가치 – The Value of Simplicity
XP가 의기투합하여 외치는 최고의 슬로건 두개는 “가능한 한 가장 단순하게 하라” 와 “너는 그것이 필요하지 않을 거야(YAGNI 로 불린다)”. 이 둘다 XP 실천인 ‘단순한 디자인’을 표현한 것이다.
YAGNI 방식은 대개 다음처럼 말한다, 내일 필요하게 될지도 모를 기능에 대해서 오늘 코딩해서는 안된다, 라고. 보기에는 이것이 쉬운 것처럼 보인다. 문제는 프레임워크, 재사용가능한 컴포넌트, 유연한 디자인과 같은 것들과 연계될때 생긴다. 이것들은 만들땐 나중에 다시 비용을 돌려받을 것이란 기대속에서, 추가적인 선행 투자(up-front)를 하게 된다. 선행투자로 유연성있게 만들겠다는 생각이 효율적인 소프트웨어 디자인의 중요한 부분처럼 보여진다.
그러나 XP의 충고는 유연한 컴포넌트나 프레임워크를 그것이 필요하게된 처음부터 만들진 말라는 것이다. 이러한 구조가 필요에 따라 키워가게 두어야 한다. 만약 오늘 Money 클래스에 더하기 기능이 필요하고 곱하기 기능은 필요치 않다면, Money 클래스에 더하기 기능만 넣어야 한다. 다음번에 곱하기 기능이 분명히 필요할 지라도, 또 그 기능 넣는게 얼마나 쉽고, 또 정말 빨리 할수 있을지라도 내일 필요한걸 오늘 넣으면 안된다. 그것을 다음번 반복(Iteration)때까지 남겨둬야한다.
이렇게 하는 첫번째 이유는 경제적인 면 때문이다. 만약 내일 필요하게 될 기능을 위해 일을 해야 한다면, 이것은 이번 반복(Iteration) 동안에 해야 할 노력을 잃는다는 것을 의미한다. 출시 계획은 지금까지 무엇을 했는가를 말하는 것이고, 미래를 위해 다른 일을 한다는 것은 개발자와 고객간의 합의에 반대하는 것이다. 여기세는 이번 반복동안에 해야할 스토리가 완료되지 못할 수도 있다는 위험요소가 있다. 만약 위험요소가 없다할지라도 부가적인 일을 해야할지는 고객의 결정에 달려 있다 – 곱셈이 계속 필요없을 수도 있다.
이런 경제적인 불이익은 우리가 불필요한 것을 추가할 수도 잇다는 가능성 때문에 더욱 커진다. 이 기능이 어떻게 작동될지를 확신하고 있더라도, 여전히 잘 못 될수가 있다 – 특히 요구사항이 상세하지 않을때에는 더욱 잘못 될수 있다. 잘못된 솔루션을 가지고 초기에 일한다는 것은 제대로 된 솔루션으로 초기에 일하는 것보다 훨씬 더 낭비이다. 그리고 XP전문가들(XPerts)은 우리가 좋아지기 보다는 더욱 나쁘게 될것같다고 일반적으로 믿는다(나도 이 의견에 역시 공감이다.)
단순한 디자인을 하는 두번째 이유는 복잡한 디자인이 단순한 디자인 보다 더욱 이해하기 어렵기 때문이다. 따라서 어떠한 시스템의 변경에서도 복잡성이 추가되어 어렵게 된다. 이것은 더욱 복잡해진 디자인이 추가되엇을 때부터 그것이 필요해지는 기간동안 비용을 증가시킨다.
현재 이런 충고는 많은 사람들에게 터무니 없이 들릴 텐데, 그들의 생각이 맞다. XP가 존재하지않는 일상적인 개발 환경에서 이렇게 생각하는 것은 당연하다. 그러나 계획된 디자인과 진화적인 디자인 사이의 균형이 변한다면, (오직 그렇게 되었을 때에만)YAGNI 는 훌륭한 실천이 된다.
요약하자면, 미래에 필요하지도 않을 새로운 기능을 추가하는데에 노력을 하지 마라. 새로운 기능을 추가하는데 비용이 전혀 들지 않더라도, 추후에 변경비용이 증가하기 때문에 그렇게는 하지 마라. 그러나 XP나 또는 그와 비슷하게 변경비용을 낮추는 테크닉을 사용할 때에만 분별있게 사용하라.
대체 단순함이란 무엇인가 – What on Earth is Simplicity Anyway
자 이제 우리는 우리의 코드가 가능한 한 단순해지기를 바란다. 어찌되었던 누가 복잡해지기를 바라겠는가. 틀림없이 이것은 이런 질문을 하게 한다. ‘단순하다는게 뭐지?’ Kent 는 XPE(extreme Programming Explained)에서단순한 디자인을 위한 4가지 규칙을 제시했다. 가장 중요한 것부터 나열하면,
- 모든 테스트를 실행하라
- 모든 의도를 나타내라
- 중복을 없애라
- 클래스나 함수의 수를 최소화하라
모든 테스트를 실행하라는 것은 굉장히 간단한 규칙이다. 중복을 없애라는 것도, 많은 개발자들에게 어떻게 하는지를 지도해야하긴 하지만, 매우 직관적이다. 애매모호한 것은 의도를 나타내라는 것인데, 정확히 이것이 무엇을 의미하는 것일까.? 여기서의 근본적인 가치는 코드의 명료성이다. XP는 읽기 쉬운 코드에 높은 가치를 둔다. XP에서 “재치있는 코드(clever code)”란 잘못사용되는 코드이다. 몇사람의 의도를 나타내는 코드가 다른 사람에게는 교묘함(cleverness)일 수 있다.
Josh Kerievsky는 그의 XP 2000 논문에서 이것에 관한 좋은 예제를 알려주었다. 그는 가장 널리 알려진 XP 코드를 살펴 보았는데 – JUnit이다. JUnit은 선택적 기능 – 병행의 동기화(concurrency synchronization)와 일괄 설치 코드(batch set up code) 같은 것들 – 을 테스트 케이스(test cases)에 추가하는데에 decorator를 사용한다. 이런 코드를 decorator로 분리함으로 일반적인 코드가 다른 것보다 훨씬 명확해진다.
그러나 결과로 나온 코드가 정말 심플한지는 스스로에게 자문해 봐야 한다. 나에겐 정말 심플했는데, 그때 난 Decorator 패턴에 친숙했기 때문이다. 그러나 다른 많은 사람들에게는 그렇지 않고 매우 복잡할 것이다. 유사하게도 JUnit은 플러그식의 함수들(pluggable methods)을 사용하는데, 대부분의 사람들이 초기에 이것이 전혀 명백하지 않은 코드라고 간파해 낸다. 그렇다면 JUnit의 디자인이 경험있는 디자이너에게는 심플하고 경험 적은 사람에게는 더욱 복잡하다고 결론지어야 하는가?
나는 중복 제거에 집중하는 것 – XP의 “한번만, 오직 한번만”과 Pragmatic 프로그래머의 DRY(너 스스로 반복하지 마라) – 은 이해하기 쉽고 참으로 훌륭한 조언이라고 생각한다. 이것을 그냥 따르기만 하면 앞길이 열릴 수 있다. 그러나 이것이 전부는 아니고, 단순함은 여전히 알아내기가 어렵다.
최근에 나는 디자인(over-designed)이 오버된 곳에서 일한 적이 있엇다. 난 그것을 리팩토링을 했고 유성성도 조금 없애버렸다. 그러자 개발자 한명이 말하길 “디자인이 없는 것을 리팩토링 하는것보다 오버-디자인된것을 리팩토링 하는 것이 더 쉽다’라고. 의도하는 것보다 좀더 단순하게 하는 것이 최고는 될수 있다. 하지만 조금 복잡하게 한다고 해서 재앙이 되는것은 아니다.
내가 들은 최고의 조언은 Uncle Bob(Rebert Martin)이 한 것이다. 그의 조언은 최고로 단순한 디자인이 어떤 것인가에 너무 매달리지 말라는 것이다. 나중에는 결국 리팩토링을 할수 있을 것이고, 해야 할 것이고, 또 하게 될것이다. 지금 가장 단순한 것이 어떤것인지 아는것 보다 리팩토링 하겠다는 의지가 훨씬 더 중요하다는 사실을 결국 알게 될것이다.
리팩토링이 YAGNI를 위반하는가? – Does Refactoring Violate YAGNI?
이 주제는 최근의 XP 메일링 리스트에 가져온 것이다. XP에서 디자인의 역할에 대해 보기 위해서 이 주제는 살펴볼 가치가 있다. 기본적으로 이 질문은 리팩토링이 기능을 추가하지는 않으면서 시간은 잡아먹는다는 점에서 시작한다. YAGNI의 관점은 미래가 아닌 현재를 위한 디자인을 하라는 것인데, 리팩토링이 이것을 위반하는가?
YAGNI의 관점은 현재 스토리에서 필요하지 않은 복잡한 것은 추가하지 말라는 것이다. 이것은 단순한 디자인의 한 부분이다. 리팩토링은 디자인은 가능한한 단순하게 유지하기 위해 필요하고, 그래서 단순하게 할수 있다 싶으면 언제든 리팩토링을 해야한다.
단순한 디자인은 XP 실천들을 이용하기도 하고 또한 실천들이 가능하게 한다. 당신이 테스팅, 지속적 통합, 그리고 리팩토링을 하기만 한다면 디자인을 효율적으로 할 수 있다. 이와 동시에 디자인을 단순하게 유지하는 것은 변경 곡선을 평평하게 하는 데에도 필수이다. 불필요한 복잡성은, 유연성을 기대하면서 넣은 것을 제외하고는, 그게 무엇이던간에 시스템을 전체적으로 변경하기 어렵게 만든다. 그러나 사람들은 예상을 잘하지 못하므로, 단순해지도록 노력하는게 최고의 선택인다. 그러나 사람들은 가장 단순한것을 처음부터 얻을수 없으므로, 목표에 가까워지도록 차근차근 리팩토링을 할 필요가 있다.
디자인 패턴과 XP – Patterns and XP
JUnit 예제는 필연적으로 패턴에 관한 얘기를 하게 한다. 패턴과 XP의 관계는 흥미롭고, 또한 공통적인 문제이기도 한다. Joshua Kerievsky 는 패턴이 XP에서는 중요하지 않다(under-emphasized)라고 설득력있게 주장하고 있으므로, 나는 여기서 다시 얘기하진 않겠다. 하지만 많은 사람들에게 있어 패턴은 XP와 대립되고 있다는 것을 마음속에 새겨두기 바란다.
이 주장의 본질은 패턴이 대부분 과용(over-used)된다는 것이다. 이 세상은 GOF를 한번 읽어보고서는 32 라인의 코드에 16개의 패턴을 집어넣은 전설적인 프로그래머로 가득차 있다. Kent와 함께 기분좋게 single malt(역주:위스키의 한 종류)를 한잔하면서 “디자인 패턴이 아닌것: 23가지의 속임수들”이라고 불리어질 논문을 작업하던 밤이 생각난다. 그때 우리는 Strategy 패턴보다는 if 문장을 사용하는 것과 같은 여러가지의 방법들에 대해 생각했었다. 위의 농담의 요점은 패턴이 대개 과용되지만, 이러한 과용이 잘못된것은 아니라는 것이다. 중요한 것은 패턴을 어떻게 사용하는가 이다.
이것에 관한 하나의 이론은 단순한 디자인의 강요가 패턴에 이르게 한다는 것이다. 많은 리팩토링이 이것을 명시적으로 보여준다 – 패턴에 대해 전혀 알지 못했다 하더라도, 그리고 패턴을 사용하지 않고 단순한 디자인의 법칙을 따를 때 조차도 결국 패턴에 이르게 된다. 이것이 사실이라고 하더라도, 이렇게 자연스럽게 패턴에 이르게 되는것이 패턴을 사용하는 가장 좋은 방법인가? 당연히, 당신이 어디로 가고 있는건지 대략이라도 알고 있고 또 모든 문제점에 대해 스스로 창출하는 대신에 조언을 해줄수 있는 책이 있다면 훨씬 좋다. 난 패턴이 필요할때면 여전히 GOF 에 손을 뻗는다. 효율적인 디자인을 위해서는 우리가 패턴의 가치에 대해서 알아야 하고 또 제대로된 사용을 위해 기술을 연마함으로 그 대가를 지불해야 한다. Joshua 가 말한것처럼, 우리는 서서히 패턴을 편하게 사용하는 방법에 대해 잘 알아야 한다. 이점에 대해서 XP는 패턴의 가치는 확실히 유지하면서, 다른 사람들과는 다른 방식으로 패턴을 사용한다.
하지만 몇개의 메일링 리스트를 읽다 보면 많은 사람들이 XP가 패턴을 삼가하라고 가르치는 것을 알고 있는 것 같다. 아이러니하겠지만 대부분의 XP의 제안자들은 패턴 단체의 리더이기도 했다. 이런 아이러니가 XP 제안자들이 패턴 저너머에 있는 것을 봤기 때문이거나, 패턴이 그들의 사고에 너무 깊이 박혀버려서 그들이 더이상 깨닫지 못하기 때문일까? 다른 사람들이 어떻게 대답할진 모르지만, 나의 대답은 “패턴은 여전히 절대적으로 중요하다”이다. XP는 개발 프로세스의 하나지만, 패턴은 당신의 프로세스가 무엇이든 간에 변함없이 가치있는, 디자인에 관한 지식의 뼈대(중심)이다.
다른 프로세스에서는 패턴을 다르게 사용할 것이다. XP는 ‘필요하기 전까지는 패턴을 사용하지 말라’는 것과 ‘단순한 구현을 거쳐 패턴으로 진화해 가라’는 것을 강조하고 있다. 패턴은 여전히 습득해야할 지식의 중요한 한 부분이다. XPers(XP 사용자들)에게 하는 패턴사용에 관한 나의 충고는 다음과 같다. 패턴을 배우는 시간을 투자하라.
패턴을 (너무 일찍이 아닌) 언제 적용 할지에 집중하라. 우선적으로 패턴의 가장 단순한 형태로 구현하는 것에 집중하고, 복잡성은 그 이후에 추가하라. 패턴을 적용한 상태에서, 나중에 이것이 단순하지 않다고 느껴진다면, 과감하게 패턴을 없애라. 나는 XP가 당연히 패턴을 더욱더 익히기를 강조해야 한다고 본다. XP의 실천에 패턴을 어떻게 맞춰야 할지는 잘 모르겠지만, Kent 가 그 방법을 알아 낼 것이라는 것은 확신한다.
아키텍처 키우기 – Growing an Architecture
소프트웨어 아키텍처가 우리에게 무엇을 의미하는가? 나에게 아키텍처는 시스템의 핵심 요소라는 개념이고, 변경되기가 쉽지 않은 부분이다. 나머지 다른 영역이 들어설 밑바탕인 것이다. 진화적인 디자인을 사용할때에 아키텍처는 어떤 역할을 하는 것인가? XP의 비평가들 또 다시 이렇게 말한다, ‘XP는 방향은 디자인 문제들을 해결하기 위해 리팩토링으로 코드를 빠르고 신뢰할수 있게 하는 것이기 때문에 아키텍처를 무시한다’고. 흥미롭게도 그들의 말이 맞다 – 그것이 XP의 약점일수도 있다. Kent Beck, Ron Jeffries, and Bob Martin 같은 대표적인 XP 지지자들은 확실히 아키텍처 디자인을 미리 하지 않으려는 데에 에너지를 더욱더 쏟고 있다. 정말 필요하다는 것을 알기 전까지는 데이타베이스를 적용하지 말고, 파일로 먼저 작업하고 이후의 반복중에 데이타베이스를 추가하는 리팩토링을 하지 말라고 가르친다.
나는 소심한 XPer(XP 사용자)이기 때문에, 난 여기에 동의할수 없다. 내 생각엔 아키텍처가 광범위한 시작점의 역할도 한다고 본다. 어플리케이션 레이어를 어떻게 나눌것인지, 데이타베이스와 (필요하다면) 어떻게 상호작용을 할것인지, 웹서버를 어떤 방식으로 다룰것인지 등이다.
본질적으로 이것들의 대부분은 우리가 수년간 익혀온 패턴의 영역이라고 생각한다. 당신의 패턴 지식이 쌓여 갈수록, 우선 그것을 어떻게 사용할지를 나름대로 결정할수 있게 된다. 그러나 주요한 차이점은 결정내린 아키텍처를 바위로 만드는 대신, 일찍 내린 결정에 잘못이 있다면 그것을 고칠수 있는 용기를 가져야 한다는 것이다. 어떤 프로젝트에서는, 출시가 임박했을때, EJB가 더이상 필요하지 않다는 결정하여 그것을 시스템에서 제거한적이 있었다. 대단히 큰 리팩토링 작업이었고, 늦게 마무리 되었지만, ‘가능케 하는 실천들’이 이것을 가능케 할 했고 또 가치있는 작업이 되게 하였다.
이것이 좀 다른 방향으로 생각해 보면 어떻게 될까. 만약 EJB를 사용하지 않을것이라 결정을 했었다면, 나중에 이것을 추가하는 것이 어려울까? EJB 없이 작업을 시도해본후 그것이 필요하다는 것을 알기 전까지는 절대로 EJB를 사용하면 안되는 것인가? 이것은 많은 요소들과 관계된 질문이다. 분명 복잡한 컴포넌트를 포함하지 않고 작업하는 것은 작업을 더욱 단순하게 하고 또 빠르게 한다. 그러나 때로는 컴포넌트를 추가하는 것보다 빼는 것이 더 쉬울때도 있다.
나의 조언은 아키텍처가 될 만한 것이 무엇인지를 판단하는 것으로 시작하라는 것이다. 다중 사용자들이 접근하는 엄청난 양의 데이타가 있다면, 첫째날 부터 데이타베이스를 사용하라. 비지니스 로직이 복잡하다는 걸 안다면, 도메인 모델을 적용하라. 하지만 단순함으로부터 멀어져서 문제가 된다는 의심에 빠지면, YAGNI 신에게 복종하라. 또한 아키텍처에 더이상 추가할 것이 없다는 것을 안다면 곧바로 아키텍처를 단순화하라.
UML과 XP – UML and XP
내가 XP와 관련되면서 듣는 질문중 가장 중요한 것은 나와 UML의 연관에 둘러싼 문제이다. XP 와 UML 은 모순되는 것이 아닌가?
모순되는 점이 많이 있다. 확실히 XP는 다이어그램의 역할을 줄이고 있다. 비록 공식적인 입장이 “다이어그램이 유용하다면 사용하라”이지만, 그 이면에는 “진짜 XPer 는 다이어그램을 사용하지 않는다”라는 의미가 내포되어있다. 이 점은 Kent 같은 사람들이 다이어그램을 불편하게 여긴다는 점에서 더욱 잘 나타난다. 실제로 난 Kent 가 정해진 표기법에 따라 자발적으로 소프트웨어 다이어그램을 그리는 것을 본적이 없다.
이 논의가 두가지 다른 원인으로부터 나왔다고 생각한다. 그 하나는, 몇몇 사람은 다이어그램이 도움이 된다고 생각하고, 또 다른 사람은 아니라고 생각한다는 사실이다. 여기서 위험한 것은, 다이어그램을 그리는 사람들은 다이어그램을 그리지 않는 사람들이 그것을 그려야 한다고 생각하는 것이고, 또 반대도 역시 그렇다는 것이다. 우리는 누군가는 그것을 필요로 하고, 누군가는 아니라는 사실만을 받아들이면 된다.
또 다른 원인은 소프트웨어 다이어그램이 무거운 프로세스와(heavyweight process) 관련되는 경향이 있다는 것이다. 이러한 프로세들은 별로 도움도 되지 않는 다이어그램을 그리는데에 많은 시간을 소비함으로서 결국 피해를 보게 한다. 그래서 나는 XPer 들이 주장처럼, “단지 해야하기 때문에” 하는 것이 아닌, 다이어그램을 속지않고 어떻게 잘 사용할 것인지에 대해 사람들이 고려해야 한다고 생각한다.
다이어그램을 잘 사용하기 위한 충고를 하겠다.
우선, 무엇을 위해 다이어그램을 그리는가를 생각하라. 그것은 바로 의사소통을 위해서이다. 의사소통을 효과적으로 한다는 말은, 중요한 것은 얻고 덜 중요한것은 버린다는 것이다. 모든 클래스를 그리지 말고 오직 중요한 것들만 그려라. 각 클래스에 대한 모든 속성과 오퍼레이션을 보여주지 말고 오직 중요한 것들만을 나타내라. 유즈 케이스와 시나리오에 대해 나올수 있는 시퀀스 다이어그램을 모두 그리지는 말라. 역시 단지 중요한 것만 그려라. 아시다시피, 일반적인 다이어그램 사용에 있어서의 문제점은 사람들이 여기에 너무 많은 정보들을 종합적으로 포함시킨다는 것이다. 소스 코드와 동기를 맞추기 가장 쉬운 것은 코드 그 자체이므로, 포괄적인 정보를 얻기 위한 최고의 위치는 코드이다.
다이어그램은 일반적으로 코딩을 시작하기전에 디자인을 미리 보기(explorer) 위해서 사용한다. 이런식의 사용이 XP와 맞지 않다고 생각할수도 있다. 근데, 사실은 그렇지 않다. 복잡하고 까다로운 작업을 할땐 먼저 디자인을 빨리 얻기 위해 코딩과 함께 다이어그램을 같이 진행하는 것도 괜찮다고 많은 사람들이 말하고 있다. 이렇게 디자인을 할때는 다이어그램을 짧게 유지하라. 모든 세부사항을 나타내려 하지 마라 (오직 중요한 것만 하라) 결과로 나온 디자인을, 최종 디자인이 아닌, 스케치로 여겨라.
마지막 항목에 대해선 좀더 설명할게 있다. 우선적 디자인(up-front design)을 하게되면, 코딩중에 필연적으로 어떤 부분이 틀렸다는 것을 발견하게 될것이다. 이것은 디자인을 변경하면 되기 때문에 그리 큰 문제가 없다. 문제는 바로 개발자들이 디자인이 끝났다고 생각한다는 것이다. 그래서 코딩중에 얻은 지식을 디자인에 다시 적용하지 않는 것이다.
디자인을 변경하다고 해서 다이어그램까지 꼭 바뀌어야 하는 것은 아니다. 디자인의 이해를 위해서 다이어그램을 그리고 난후 그것을 버려도 된다. 그것을 그려서 도움을 받았다면, 그것만으로도 충분히 가치를 한것이다. 그것들은 영구히 보존할 공예품(artifacts)일 필요는 없다. 최고의 UML 다이어그램은 공예품(artifacts)이 아니다.
많은 XPers(XP 사용자들)는 CRC 카드를 사용한다. 이것은 UML과 마찰하는 부분이 없다. 난 CRC 와 UML 중 어떤것이 작업에 더 유용하던지 간에, 항상 이 둘을 섞어서 사용한다
UML 다이어그램의 또 다른 사용예는 문서작업(documentation)을 진행중(on-going)일때 이다. 다이어그램은 일반적인 형식으로 case tool 의 모델로서 존재하게 된다. 이 문서가 사람들이 시스템에서 작업할때 도움을 줄것이라고 생각하는데, 실제로는(in practice) 전혀 도움이 되지 않는다. 최신 버전으로 유지하는데 시간이 많이 걸리므로, 코드와 동기화하기가 힘들다.
다이어그램이 CASE tool 이나 두꺼운 바인드 안에 숨어있으므로 아무도 그걸 보려고 하지 않는다.
문서작성(documentation)과 관련된 이런 문제들을 해결할 나의 제안은:
- 큰 노력없이 최신버전으로 유지할수 있을 때만 다이어그램을 사용하라.
- 모든 사람들이 쉽게 볼수 있는 곳에 다이어그램을 놔두어라. 난 벽에 붙이는걸 좋아한다. 그리고 간단한 변경같은 것은 벽에다가 바로 수정할수 있도록 한다.
- 사람들이 다이어그램을 사용하고 있는지 지켜봐라. 아무도 안쓰고 있다면 던져 버려라
UML 사용에 있어서 생각해 볼 수 있는 마지막 관점(aspect)은, 다른 그룹으로 문서를 넘겨줄때 이다. XP는 문서를 여타 다른 스토리처럼 다룬다. 그래서 문서의 가치는 고객에 의해 결정된다. 여기서 UML이 고객과의 의사소통에 도움을 주기때문에 유용하다고 말할 수 있다. 기억할 것은, 자세한 정보를 모두 보관하고 있는 곳은 코드라는 것과, 다이어그램은 중요한 이슈를 요약하고 강조하는 데에 사용해야 한다는 것이다.
메타포에 대해 – On Metaphor
휴.. 이것에 대해 공개적으로 얘길 한적이 있지만, 여전이 이 메타포라는 것을 어떻게 사용하는지 모르겠다. 이것이 제대로 작동하고(work), 또 C3 프로젝트에서 매우 잘 작동(work)했다는 것도 봤지만, 여전히 어떻게 된건지 전혀 모르겠다. 어떻게 하는 것인지 그냥 얘기해 보도록 하겠다.
XP의 메타포는 워드 커닝햄(Ward Cunninghams)에 의해 만들어졌는데, 네임 시스템(system of names) 접근법으로부터 시작되었다. 요점은 어떤 도메인(domain)에 대해 이야기할때 잘 알려진 이름을 사용해서 표현하는 것이다. 네임 시스템은 클래스나 메소드의 이름을 짓는 방식과 비슷하게 동작한다.
난 도메인에 대한 개념적 모델을 만들어서 네임시스템을 구축한 적이 있다. 이때 도메인 전문가와 함께 일을 했었다. 이렇게 구축하는 것이 굉장히 주의를 요하는 일이라는 걸 알게 되었다. 표기법은 최대한 적게 또 간단하게 유지해야 하며, 은근슬쩍 모델에 들어가려고 하는 기술적 사항들(issues)로부터 보호해야한다. 만약 당신이 이렇게 할수 있다면, 도메인 전문가가 이해할 수 있는 도메인 용어사전(vocabulary)을 만들기 위해 이것을 사용할 수 있다. 그리고 개발자와의 의사소통을 위해 사용할 수 있다. 모델이 클래스 디자인과 완벽하게 매칭되진 않겠지만, 전체 도메인에 대한 일반적인 용어사전(vocabulary)을 제공한다는 것만으로 충분하다.
임금지불(payroll)을 공장 조립 라인(factory assembly line)에 비유한 C3 메타포(metaphor)처럼, 이 용어사전(vocabulary)도 거의 동일하게 메타포적이라고 나는 생각한다. 그리고 또한, 도메인(domain)의 용어사전을 네임시스템(system)의 바탕으로 하는 것도 그리 나쁜 생각이 아니라고 본다. 또한 이름들의 시스템을 얻는데 잘 적용 되었던 기법들을 포기하고 싶은 생각도 없다.
적어도 시스템의 윤곽(outline)에 관한 디자인은 필요하다는 이론으로 사람들은 종종 XP 를 비판한다. XP 사용자들(XPers)은 “그것이 메타포이다”라고 응답하곤 한다. 하지만 여전히 난 메타포가 설득력있게 설명된 적이 없다고 생각한다. 이게 바로, XP 가 해결해야 할 현실적인(real) 빈틈이다.
커서 아키텍트가 되길 원하는가?
지난 십년 간 대부분, “소프트웨어 아키텍트(software architect)”라는 용어는 유명해졌다. 개인적으로는 어려운 용어이다. 나의 부인은 구조 공학자(structure engineer)이다. 엔지니어(Engineer)와 아키텍트(architect)의 관계는 … 흥미로운 것이다. 내가 가장 좋아하는 이야기는 “아키텍트(architect)는 세가지 B들에 도움이 된다: 식물의 뿌리들(bulbs), 식물들(bushes), 새들(birds)” 이다. 이것의 의미는 아키텍트는 이러한 모든 예쁜 그림을 그리지만, 실제로 이를 가능케 하는 건 엔지니어(engineer)들이라는 것이다. 나는 결국 소프트웨어 아키텍트(software architect)라는 용어를 기피하기로 했다. 내 부인이 나를 전문 직업인으로써 존중해주지 않는다면, 내가 아키텍트라고 말한 들 무슨 소용이 있겠는가?
소프트웨어에서, 아키텍트라는 용어는 많은 것들을 의미한다. (소프트웨어 분야에서는 어떤 용어든지 많은 것들을 의미한다.) 하지만 일반적으로, 좀 진지함을 섞어서, 이 아키텍트라는 말은,“나는 단순한 프로그래머가 아니라 – 아키텍트입니다.”라고 말하는 것이다. 이는 “나는 지금 아키텍트입니다, 나는 아무 프로그래밍이나 하기엔 너무 중요한 존재입니다.”라는 식으로 해석될 것이다. 문제는 이런 평범한 프로그래밍으로부터 차별화하고, 테크니컬한 리더쉽(technical leadership)을 훈련하고자 할때는 어떤 노력이 필요한가를 스스로에게 물어 봐야 할 것이다.
스스로에게 물어본다면 많은 감정을 느낄 것이다. 많은 사람들이 더 이상 아키텍트로서의 역할이 없다고 투덜거리기도 한다. “XP에는 노련한 아키텍트가 설 자리가 없어” 라는 말을 종종 듣는다.
디자인 자체의 역할이 많기 때문에, XP가 경험이나 훌륭한 디자인 기술 (skill)을 무시한다고 생각하지 않는다. 실제로 나는 많은 XP 지지자들(proponents)(Kent Beck, Bob Martin, Ward Cunningham)로부터 디자인에 무엇이라는 것을 배웠다. 하지만 그들의 역할은, 많은 사람들이 기대하는 기술적 리더쉽의 역할로부터 다른 역할로 바뀌었다.
예로서, ThoughtWorks에 있는 우리회사의 기술적인 리더(technical leader)들 중의 한명에 대해 말하겠다: Dave Rice. Dave는 몇 개의 프로젝트의 라이프 사이클(life-cycle)들을 거쳤으며, 50명이 참가하는 프로젝트에서 비공식적으로 이들을 이끌어 가고 있다. 그의 리더(leader)로서의 역할은 모든 프로그래머(programmer)들과 함께 많은 시간을 보내는 것이다. 그는 프로그래머가 도움이 필요할 때면 그들과 같이 작업하며, 누가 도움을 필요로 하는지를 살핀다. 그의 자리가 그를 가장 잘 나타낸다. 오랜 기간동안 ThoughtWorks에서 일해왔기 때문에, 그가 좋아하는 어떤 사무실도 그는 가질 수 있었다. 그는 출시 관리자(release manager)인 Cara와 함께 사무실을 썼다. 그러나, 지난 몇개월 전에, 그는 프로그래머들이 일하는 열린 공간으로 옮겼다 (XP가 선호하는 “열린 작업실 (open war room)”을 사용하여) 이런 방법을 통해서 어떤 일이 진행 중인지를 살필 수 있고, 필요할 때마다 도와 줄 수 있기 때문에, 이는 그에게 중요하다.
XP를 아는 사람들은 내가 XP 코치(Coach)의 명백한 역할을 설명하고 있다는 것을 알게 될 것이다. 사실 XP에서 하는 말장난중 하나는 기술적인 리딩(technical leading)을 하는 사람을 “코치(Coach)”라고 부른다는 것이다.. 이 의미는 분명하다: XP에서 technical leadership은 programmer들을 가르치고 그들의 결정을 돕는 것을 통해 보여준다. 이는 훌륭한 테크니컬 기술(skill)뿐 아니라 뛰어난 사람을 다루는 기술(skill) 역시 요구하는 것이다. XP 2000에서 Jack Bolles가 말했다. ‘단독의 대가(lone master)들이 설 자리는 이제 거의 없다’라고. 협동(Collaboration)과 가르침(teaching)이 성공의 열쇠이다.
콘퍼런스(Conference)의 저녁 만찬에서, Dave와 나는 XP를 반대하는 한 사람(a vocal opponent)과 토론을 했었다. 우리가 이룬 것들에 대해서 토론해 가면서, 서로의 접근 방식이 유사하다는 것을 깨달았다. 우리는 모두 적응적이고 반복적인 (adaptive and iterative) 방법을 좋아하였다. 테스팅(Testing)도 중요했다. 그래서 우리는 그가 왜 그렇게 격렬하게 반대하는 지 이상하게 생각되었다. 그러자, 그는 “내가 가장 원하지 않는 것은 내 프로그래머들이 디자인을 가지고 리팩토링하면서 장난치는 것(monkeying) 것이다”라고 말하였다. 이제 모든 것이 분명해졌다. Dave가 나중에 이런 말을 나에게 했다. “자신의 프로그래머(programmer)들을 신뢰하지 않는 다면 왜 그는 그들을 고용한 거지?”. 관념의 격차 (conceptual gulf)는 이로서 명백해졌다. XP에서 노련한 개발자가 할 수 있는 가장 중요한 것은, 가능한 많은 기술(skill)을 경험이 부족한 개발자(junior developer)들에게 전달하는 것이다. 중요한 결정을 내리는 아키텍트(Architect) 대신, 개발자들이 중요한 결정을 내릴수 있도록 가르치는 코치(coach)가 되어야 한다. Ward Cunningham이 지적한 것처럼, 그의 기술이 확장(amplify)되면, 뛰어난 사람(hero) 혼자서 하는 것보다 더 많은 것을 프로젝트에 추가할 수 있다.
돌이킬수 있는 (or 취소 가능성) – Reversibility
XP 2002 에서 Enrico Zaninotto 는 agile method와 lean manufacturing 을 함께 섞어서(tie-ins) 쓰는 것에 관한 매혹적인 토론을 했었다. 그의 시각은, 프로세스 안에서 돌이킬 수 없는(irreversibility) 것을 줄임으로써 복잡함을 다룬다는 것이 이 두 방법의 핵심중의 하나라는 것이었다.
이 시각에선 복잡함의 근원이 ‘돌이킬수 없는 결정’ 이라고 보고 있다. 결정을 쉽게 바꿀수 있다면, 올바르게 만든다는 것이 덜 중요한 문제가 될것이고, 인생이 더욱 편해질 것이다. 진화적인 디자인의 결과로서, 설계자(designers)들은 그들의 결정이 돌이킬 수 없는(irreversibility) 상황이 되는 것을 피하는 방법에 대해 충분히 고려해야 한다. 현재 올바른 결정을 위해 노력하기 보다는, 좀더 많은 정보를 얻기 전까지 결정을 미루는 방법을 찾거나, 나중에 큰 어려움없이 결정을 뒤바꿀수 있게 끔 결정을 내려야 한다.
애자일 방법론(agile methods)에서 소스 코드와 그 외 모든것을 소스 코드 관리 시스템에 넣는 것은 이 때문이다. 예전 코드로, 특히 아주 오래전의 결정으로 인해 들어갔던 코드로, 돌아 갈 수 있다면, (비록 자주 사용되지는 않을지라도) 팀에게 신뢰를 주는 밑바탕이 될것 이다.
돌이킬 수 있는 디자인은 또한 에러가 빨리 나타나게 하는 프로세스이기도 하다. 반복적인 개발(iterative development)이 가치있는 이유중 하나는 빠른 반복을 통해 고객이 시스템이 커가는 것을 볼 수 있고, 요구사항 중의 실수가 나중에 훨씬 심각한 비용을 치루기 전에 고쳐질 수 있다는 점이다. 디자인에 있어서도 이런 빠른 오류 발견은 중요하다. 이것은, 어떤 문제가 생겼을때 잠재적인 문제 영역까지도 빠르게 검사할 수 있도록 무언가를 당신이 구축(set things up)해야 한다는 것을 의미한다. 또한 지금 당장 변경을 하진 않을지라도, 미래의 있을 변경이 얼마나 어려운지 알기 위해 실험도 해봐야 할 것이다. 시스템의 브랜치에서 일회용 프로토타입을 만들어 효율적으로 실험 할 수 있다. 몇몇 팀은 미래의 변경될 사항을 미리 프로토타입 해 봄으로써, 그 변경이 얼마나 어려울 수 있는 지에 관한 연구결과를 가지고 있다.
디자인을 향한 의지 – The Will to Design
이 글에서 테크니컬한 실천사항(practices)에 대해 많이 집중했지만, 한가지 간과하기 쉬운 부분이 있다. 바로 사람이다. 진화적인 디자인이 제대로 되기 위해서는, 거기에 집중하는 노력이 필요하다.
이 노력은 오직 사람만이 할수 있다. 팀에 있는 누군가가 높은 디자인 품질을 위해서 결단과 노력을 해야 한다. 모든 사람이 의지를 가질 필요는 없다(비록 그렇다면 좋긴 하겠지만). 일반적으로 팀의 한 두 사람만이 전체 디자인을 유지하는 책임이 있다. 이것이 보통 ‘아키텍트’의 일 중 하나다. 여기서의 책임은 기반 코드(code base)에 대해 예리한 시선을 유지하고, 자칫 혼란스러워 질수 있는 영역을 찾아내고, 그 영역이 제어할 수 있는 범위를 벗어나기 전에 빨리 대응하는 것이다. 디자인은 유지하는 사람이 그 디자인을 고칠 필요는 없다. 그러나 누군가 고쳤다는 것을 확실히 알아야 한다.
디자인 의지의 부족이 진화적인 디자인을 실패하게 하는 가장 큰 이유이다. 이 글에서 말하는 내용들을 여러분이 안다고 하더라고, 디자인 의지가 없이는 되지 않는다.
리팩토링 하기 어려운 것들 – Things that are difficult to refactor in
리팩토링을 모든 설계(design)의 결정을 처리하기 위해 사용할 수 있는가? 또는 문제가 너무나 깊이 스며들어(pervasive) 있어서 나중에 추가하기 곤란한 것도 있는가? 현재, XP의 신념(orthodoxy)에 따르면, 모든 것들은 이후에 추가하기 쉬우며, 그렇기 때문에 YAGNI는 항상 적용된다. 혹 예외가 있지 않을까 나는 의심한다. 나중에 추가하는 것에 위배되는 좋은 예는 국제화(Internationalization)이다. 이런 경우는 지금 당장 해야 하는 것을 나중에 추가하려고 노력하는 것 아닌가?
나는 이러한 영역(category)에 해당하는 것들을 쉽게 생각해 낼 수 있다. 그러나, 여전히 데이타(data)가 거의 없다는 것이 현실이다. 국제화(internationalization)와 같은 무언가를 나중에 추가해야만 한다면, 그렇게 하는데 드는 노력이 상당하다는 것을 당신은 알 것이다. 실제로 필요하게 되기 전에 미리 넣도록 하면, 여러 주가 지날수록, 그에 대해 덜 의식하게 된다. 또한, 잘못될수 있다는 사실에 대해서도 대해 덜 의식하게 되고, 그리하여 어쨌든 약간의 리팩토링(refactoring)이 필요하게 될 것이다.
YAGNI를 부분적으로 정당화 시키는 것은, 이러한 많은 잠재적인 필요성들이 실제로 필요하지 않을 수도 있고, 적어도 예상했던 바와는 달라진다는 사실이다. 국제화와 같은 것들을 하지 않아서 아낄 수 있는 노력이, 실제로 필요하여 리팩토링(refactoring)을 하는데 필요한 노력보다 작다.
깊이 생각해볼 또 다른 문제는 어떻게 하는지를 정확히 알고 있느냐 하는 것이다. 여러 번 국제화(internationalization)를 해보았다면, 사용할 패턴들을 알 것이다. 이 같은 경우는 제대로 할 가능성이 더 높다. 그러한 상태라면, 예상되는 구조(anticipatory structure)를 추가하는 것이 문제를 새롭게 경험하는 것 보다 더 나을 것이다. 그러므로 당신이 방법을 아는 경우라면 지금 하는 것과 나중에 하는 것의 비용을 결정할 수 있는 위치에 있을 것이라고 생각한다. 그러나, 전에 한적이 없다면, 가격을 제대로 산출할 수 없을 뿐더러, 제대로 그 작업을 하기 어렵다. 이런 경우라면 나중에 추가해야만 하다. 그 때가서 추가하고, 그리고 나서 어려웠음을 느끼면, 아마도 일찍 추가 시키는 편이 좋았을 것이라고 생각할 것이다. 팀은 더욱 노련해 지고, 도메인(domain)을 더 잘 알게 되며, 요구사항을 보다 더 이해하게 될 것이다. 이러한 위치가 되면, 얼마나 쉽게 해결할 수 있을 뻔 했을지를 돌아보게 된다. 일찍 추가하는 것이 생각하는 것보다 더 어려울 것이다.
이는 또한 이야기의 순서(ordering of stories)와 연결된다. Planning XP 책에서 Kent 와 나는 우리의 불일치를 공공연하게 표시하였다. Kent는 이야기들의 순서에 대한 요소(factor)로 비즈니스 가치만을 평가하는 걸 선호 한다. 초기에는 동의하지 않았지만, Ron Jeffries는 이제 이러한 것에 동의한다. 나는 여전히 동의하지 않는다. 나는 비즈니스 가치와 기술적 위험성(technical risk) 사이의 균형점이 이야기들의 순서를 정하는 요소라고 믿는다. 이러한 생각이 나로 하여금 적어도 국제화 같은 것들은 초기에 그러한 기술적 위험성(risk)를 완화시켜야 된다고 생각하게 하였다. 그러나, 이것은 국제화가 첫번째 출시에 필요한 경우에만 사실이다. 가능한 빨리 출시하는 것은 매우 중요하다. 첫 출시에 필요한 것이 아니라면, 모든 추가적인 복잡성은 첫 출시 이후로 미룰만한 가치가 있다.
상품화 되고 실행되는(shipped and running) 코드(code)의 힘은 대단하다. 이는 고객의 관심을 모으고, 신뢰성을 높이며, 거대한 학습원(massive source of learning)이 된다. 출시일을 앞당기도록 모든 노력을 기울여라. 첫 출시 이후에 추가적인 노력을 하더라도, 출시를 앞당기는 편이 낳다.
새로운 기술(technique)은 경계 조건(boundary conditions)이 불분명 한게 당연하다. 많은 XP 사용자들은 진화적인 디자인이 특정 문제에는 불가능하다고 말하고 있다. ‘불가능’을 정복하다 보면 극복 못할 문제는 없다는 확신이 든다. 물론 이렇게 일반화 시킬 수는 없겠지만, XP 공동체에서 이러한 경계 영역에 도전하여 실패하기 전까지는, 모든 것들이 리팩토링이 가능하다고 봐야 할 것이다.
디자인이 제대로 되고 있는가? – Is Design Happening?
진화하는 디자인의 어려움 중의 하나는 실제로 디자인을 제대로 하고 있다고 꼭 짚어서 말하기가 어렵다는 것이다. 디자인과 프로그래밍을 서로 섞어서 하다보면 디자인이 없이도 프로그래밍을 할수 있다는 위험이 있다 – 이것이 진화하는 디자인을 이탈하여 실패하는 상황이다.
당신이 개발팀에 있다면, 디자인이 기반 코드(code base)의 품질에 의해 나타나는지를 알수 있다. 만약 기반 코드가 더욱 복잡해지고 작업하기가 어려워진다면, 충분히 디자인을 하지 않았다는 것이다. 슬프게도 이것은 주관적인 의견이고, 디자인의 품질에 관한 객관적이고 신뢰할 만한 측정기준이 없다.
이런 근거자료의 부족은 전문가들을 어렵게 하고, 팀의 비전문가들을 더욱 더 당황스럽게 한다. 만약 당신이 관리자나 고객이라면 소프트웨어가 잘 디자인 되었다는 것을 어떻게 말할수 있을까? 어설프게 디자인된 소프트웨는 추후 변경에 따른 비용이 많이 들기 때문에 분면 문제가 되기 때문이다. 이것을 쉽게 대답 할수는 없겠지만, 약간의 힌트는 있다.
전문가들에게 귀를 귀울여라. 변경하기가 힘들다고 그들이 불평한다면, 그들의 말을 진지하게 받아들이고 그것을 고쳐나갈 시간을 주어라. 코드를 어떻게 내던져 버리는지를 주시하고 관찰하라. 왕성하게 리팩토링하는 프로젝트는 나쁜 코드들은 꾸준히 제거해 나갈 것이다. 만약 제거할 것이 없다면 이건 분명히 리팩토링이 제대로 되고 있지 않다는 신호이다 – 디자인은 타락하게 될 것이다.
다른 여러 측정자료들처럼 이것도 역시 남용될수 있는데, 뛰어난 전문가들도 그 자료가 주관적임에도 불구하고 여기저기에 퍼뜨린다.
그래서, 디자인은 죽었는가? – So is Design Dead?
전혀 그렇지 않다. 다만 디자인의 성향이 바뀐것이다. XP 디자인은 다음과 같은 기술을 요구한다.
- 코드를 최대한 명확하고 단순하게 유지하려는 부단한 의지
- 필요할때 자신있게 개선시킬수 있는 리팩토링 기술
- 패턴에 관한 훌륭한 지식: 그냥 해결책으로 보는것 뿐만 아니라 언제 그것을 사용하고, 어떻게 차츰 발전시킬지를 날카롭게 판단하여야 한다.
- 현재 내려진 결정이 나중에는 변하게 될수 있다는 것을 알고, 미래의 변화에 항상 눈을 뜨고 디자인을 하는 기술.
- 디자인을 꼭 이해해야 하는 사람에게 코드나 다이어그램 특히 ‘대화’를 통해서 전달하는 방법을 아는 것.
이런 기술이 두렵게 느껴질수도 있다. 하지만 훌륭한 디자이너(설계자)에게는 항상 고통과 노력이 따른다. XP가 이 고통을 조금도 줄여주지는 않는다 – 나에겐 그랬다. 하지만 XP가 효율적인 디자인을 위한 새로운 길은 가르쳐 주었다고 생각한다. 진화하는(evolutionary) 디자인이 그것이다. 나는 진화를 아주 좋아한다. 만약 진화가 없다면 나도 없는 것이다.(미래는 없는 것이다.)
감사의 글 – Acknowledgments
나는 최근 몇년동안 많은 훌륭한 사람들로부터 좋은 아이디어를 얻어왔다. 그중 대부분은 기억의 저편으로 사라져 버렸지만, Joshua Kerievsky의 멋진 아이디어는 아직도 기억한다. 또한 Fred George와 Ron Jeffries의 유용한 의견들도 아직 기억한다. 또 Ward 와 Kent 로부터 얼마나 많은 좋은 아이디어들이 나왔는지도 잊을수 없다.



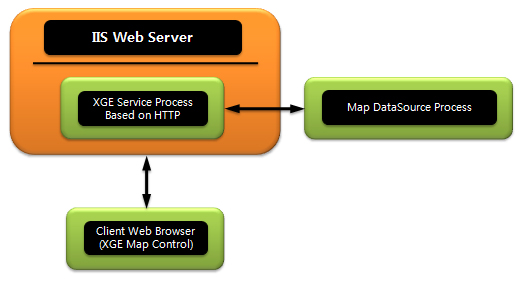 위의 그림에서는 언급되지 않았지만, 이럴때를 위해 Monitor 프로세스가 존재하며 이 XGE Monitor 프로세스가 하는 일은 DataSource 프로세스가 살아있는지를 일정한 시간 간격으로 검사하고 죽어있다면 다시 DataSource 프로세스를 살려주는 역활을 합니다. 역활에 따라 적절하게 프로세스로 분리한 이러한 구조로 어떤 상황에서도 죽지 않는다라는 이상적인 목표에 많이 접근할 수 있을 것으로 판단됩니다. 끝으로 XGE 웹서비스는 매우 구조가 간단합니다. 구조가 간단하기에 안정성과 빠른 응답성은 물론이고 확장성의 이점까지 두루 얻을 수있습니다. 일단 위의 그림 역시 매우 간단한 구조인데, 이 그림을 구성하고 있는 XGE 서비스와 DataSource 프로세스에 대한 구조에 대한 그림을 살펴보면, 얼마나 간단한지 알 수 있을겁니다.
위의 그림에서는 언급되지 않았지만, 이럴때를 위해 Monitor 프로세스가 존재하며 이 XGE Monitor 프로세스가 하는 일은 DataSource 프로세스가 살아있는지를 일정한 시간 간격으로 검사하고 죽어있다면 다시 DataSource 프로세스를 살려주는 역활을 합니다. 역활에 따라 적절하게 프로세스로 분리한 이러한 구조로 어떤 상황에서도 죽지 않는다라는 이상적인 목표에 많이 접근할 수 있을 것으로 판단됩니다. 끝으로 XGE 웹서비스는 매우 구조가 간단합니다. 구조가 간단하기에 안정성과 빠른 응답성은 물론이고 확장성의 이점까지 두루 얻을 수있습니다. 일단 위의 그림 역시 매우 간단한 구조인데, 이 그림을 구성하고 있는 XGE 서비스와 DataSource 프로세스에 대한 구조에 대한 그림을 살펴보면, 얼마나 간단한지 알 수 있을겁니다.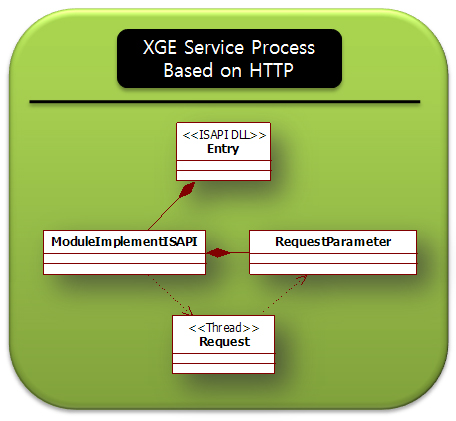
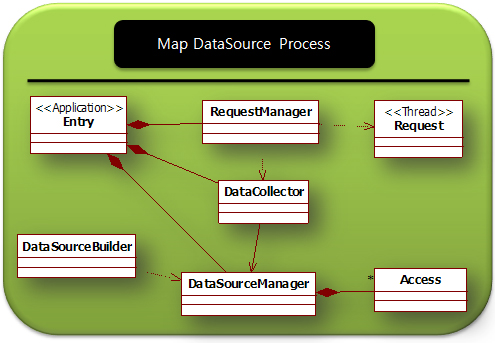 위의 그림은 UML 중 Class Diagram입니다. 실제로 개발한 프로젝트에서 사용한 클래스의 모든 것입니다. 물론 기능 확장등으로 몇가지 더 추가되겠지만.. 요청과 그에 대한 처리라는 관점에서 봤을때 새로운 클래스를 추가하는 상황은 최대한 배제하도록 설계가 되었습니다. 이러한 설계의 단순함으로 인해 전체적으로 구조가 간단해졌으며, 앞서 언급한 안정성, 빠른 응답성, 확정성의 이점을 얻을 있겠지요. (참고로 위의 UML은 StarUML로 작성했습니다. 국산 공개 소프트웨어)
위의 그림은 UML 중 Class Diagram입니다. 실제로 개발한 프로젝트에서 사용한 클래스의 모든 것입니다. 물론 기능 확장등으로 몇가지 더 추가되겠지만.. 요청과 그에 대한 처리라는 관점에서 봤을때 새로운 클래스를 추가하는 상황은 최대한 배제하도록 설계가 되었습니다. 이러한 설계의 단순함으로 인해 전체적으로 구조가 간단해졌으며, 앞서 언급한 안정성, 빠른 응답성, 확정성의 이점을 얻을 있겠지요. (참고로 위의 UML은 StarUML로 작성했습니다. 국산 공개 소프트웨어)