[카테고리:] 프로그래밍

플래시 빌더의 단점은 협업 개발이 어렵다는 것입니다. 사실.. 아직까지도 플래시에서 모듈을 통한 협업 개발이 충분한가라는 점에서.. 실제 프로젝트에 적용해보기 전까지는 확신할 수는 없지만 파악해본 바로는 충분히 가능하다.. 라고 판단됩니다.

메인 어플리케이션 프로젝트가 있고.. 이 메인 어플리케이션에서 사용하는 또 다른 별도의 모듈을 위한 프로젝트(모듈 프로젝트)가 있다고 하겠습니다. 모듈 프로젝트는 일반적인 플렉스 프로젝트(Flex Project)로 생성합니다.

이 모듈 프로젝트에 2개의 모듈을 추가하도록 하겠습니다. 첫번째는 단순히 함수만을 제공하는 모듈 클래스이고 두번째는 UI를 제공하는 모듈 클래스입니다. 먼저 함수만을 제공하는 모듈 클래스는 ActionScript Class로 해서 생성하며 클래스명은 Module1으로 지정하고 Super Class로는 반드시 ModuleBase로 지정합니다. 생성된 Module1.as 파일을 다음처럼 코딩합니다.

package
{
    import mx.modules.ModuleBase;
 
    public class Module1 extends ModuleBase
    {
        private var arg:Number = 1;
  
        public function Module1(arg:Number)
        {
            super();
            this.arg = arg;
        }
  
        public function sum(a:Number, b:Number):Number
        {
            return (a + b) * arg;
        }
    }
}

모듈 클래스의 생성자가 하나의 인자를 갖습니다. 그리고 sum이라는 함수를 제공합니다. 매우 단순한 모듈 클래스입니다. 이 모듈 클래스는 컴파일되어 Module1.swf 파일로 만들어져야 합니다만 확장자가 as는 자동으로 모듈로 만들어지지 않으므로 모듈 프로젝트의 속성창에서 Flex Modules에서 추가해야 합니다.

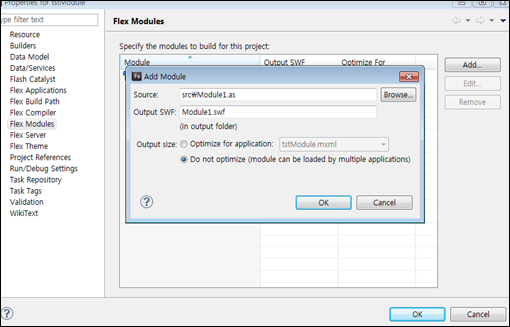
추가할때 Output Size 옵션을 Do not optimize로 선택해서 다양한 많은 어플리케이션에서 활용될 수 있도록 지정합니다.

이제 추가된 모듈 클래스인 Module1을 별개의 어플리케이션 프로젝트에서 사용해 보도록 하겠습니다. 버튼을 클릭했다고 할때 Module1 모듈 클래스를 활용하는 방식으로 하겠습니다. 버튼 클릭시 실행되는 코드는 다음과 같습니다.

private var iModuleInfo:IModuleInfo;
protected function onTest(event:MouseEvent):void
{
    iModuleInfo = ModuleManager.getModule(
        "../../eTAS_Modules/tstModule/bin-debug/Module1.swf");
    iModuleInfo.addEventListener(ModuleEvent.READY, onModuleReady);
    iModuleInfo.addEventListener(ModuleEvent.ERROR, onModuleError);
    iModuleInfo.load();
}

5번째 줄에 모듈 프로젝트에서 생성된 Module1.swf를 지정하고 있습니다. 로컬에서 테스트할때는 이렇게 폴더 경로로 사용되지만 실제로 웹서버에 올려질때는 URL 경로가 사용됩니다. 모듈의 준비가 잘되었을때 실행되는 onModuleReady와 실패했을때 실행되는 onModuleError 함수는 다음과 같습니다.

private function onModuleReady(e:Event):void
{
    e.target.removeEventListener(ModuleEvent.READY, onModuleReady);
    e.target.removeEventListener(ModuleEvent.ERROR, onModuleError);
    
    var mainClassName:String = iModuleInfo.factory.info().mainClassName;
    
    var mainClass:Class = 
        iModuleInfo.factory["getDefinitionByName"](mainClassName) as Class;
    var module:Object = new mainClass(100); 

    text.text = module.sum(100, 200);
 }
   
private function onModuleError(e:Event):void
{
    e.target.removeEventListener(ModuleEvent.READY, onModuleReady);
    e.target.removeEventListener(ModuleEvent.ERROR, onModuleError);
    
    // ERROR 
}

6번에서 모듈의 클래스명을 가져오고 이 클래스 명으로부터 실제 클래스 타입을 8번 코드를 통해 얻습니다. 그리고 이 클래스 타입을 통해 실제 인스턴스를 10번 코드를 통해 생성합니다. 그리고 12번 코드처럼 사용합니다.

이제 다음으로 UI를 제공하는 모듈에 대한 생성과 사용에 대해서 정리해 보겠습니다. 모듈 프로젝트에서 MXML Module로 하여 새로운 파일을 생성합니다.
 

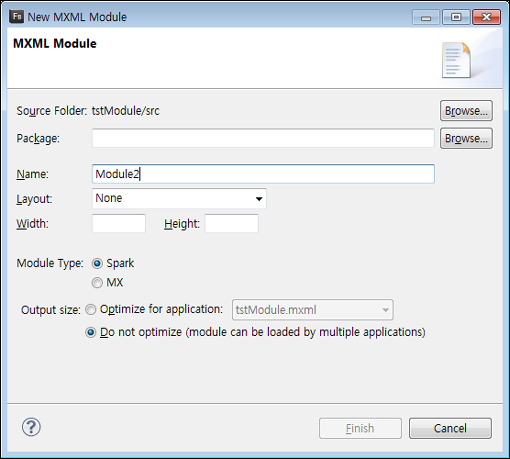
파일명은 Module2로 하고 Output Size 옵션을 Do not optimize로 하여 다른 많은 프로젝트에서 재활용할 수 있도록 합니다. 생성된 Module2.mxml을 다음처럼 코딩합니다.

  xmlns:s="library://ns.adobe.com/flex/spark" 
    xmlns:mx="library://ns.adobe.com/flex/mx">
 
    
                    import geoservice.XrMap;
   
            private var map:XrMap = null;
   
            public function setup(map:XrMap):void
            {
                this.map = map;
            }
   
            protected function onClick(event:MouseEvent):void
            {
                map.coordMapper.setMapScale(500);
                map.update();
            }
        ]]>

하나의 버튼 컴포넌트를 배치했고 이 버튼에 대한 클릭 이벤트를 지정했습니다. 그리고 setup이라는 함수를 하나 추가해서 이 UI 모듈의 코드들이 실행하기 위해 필요한 설정값들을 지정할 수 있도록 하였습니다.

이 Module2에 대한 모듈 UI를 별도의 어플리케이션 프로젝트에 사용해 보도록 하겠습니다. 어클리케이션 프로젝트의 메인 mxml에 다음과 같은 UI 컴포넌트를 추가합니다.

네! 바로 앞서 만들어 놓은 Module2 모듈 UI가 들어갈 자리입니다. id는 modLoader로 했음을 기억합시다! 버튼을 클릭하면 이 modLoader에 앞서 만들어 놓은 UI 모듈을 올려 보도록 하겠습니다.

protected function onTest(event:MouseEvent):void
{
    modLoader.addEventListener(ModuleEvent.READY, onUIModuleReady);
    modLoader.addEventListener(ModuleEvent.ERROR, onUIModuleError);
    modLoader.url = "../../eTAS_Modules/tstModule/bin-debug/Module2.swf"
}

모듈 로딩이 성공했을때와 실패했을때에 대한 이벤트 리스너를 지정했고 modLoader의 url 속성에 적재할 UI 모듈에 대한 경로와 파일명을 지정했습니다. 로컬에서는 이처럼 디렉토리 경로지만 실제 웹서버에 올라가면 URL 경로로 변경해줘야 합니다. 모듈 로딩이 성공했을때와 실패했을때에 대한 이벤트 리스너의 코드는 다음과 같습니다.

private function onUIModuleReady(e:Event):void
{
    modLoader.removeEventListener(ModuleEvent.READY, onModuleReady);
    modLoader.removeEventListener(ModuleEvent.ERROR, onModuleError);
    
    modLoader.child.addEventListener(FlexEvent.CREATION_COMPLETE, 
        onUIModuleCreateCompleted);
}

private function onUIModuleError(e:Event):void
{
    modLoader.removeEventListener(ModuleEvent.READY, onUIModuleReady);
    modLoader.removeEventListener(ModuleEvent.ERROR, onUIModuleError);
    
    // ERROR!
}

모듈이 성공적으로 로딩이 되면 6번 코드처럼 UI 모듈을 구성하는 UI가 생성되는 이벤트 리스너를 지정해야 합니다. UI가 생성되는 이벤트 리스너 함수인 onUIModuleCreateCompleted의 코드는 다음과 같습니다.

private function onUIModuleCreateCompleted(e:Event):void
{
    modLoader.child.removeEventListener(FlexEvent.CREATION_COMPLETE, 
        onUIModuleCreateCompleted);
    
    var ui:Object = modLoader.child;
    ui.setup(map);
}

7번 코드가 바로 앞서 UI 모듈에서 추가했던 함수입니다. UI 모듈의 버튼을 클릭하면 지정된 코드가 실행되게 됩니다.

비록…. 모듈에 대한 설명예를 단순하게 들었지만 필요한 것들에 대해서 최소한으로.. 그리고 필요한 모든 것을 설명한듯합니다. 물론 실전에서 적용해보고 부족한 부분에 대해서 덧붙이도록 하겠습니다.