[카테고리:] Algorithms

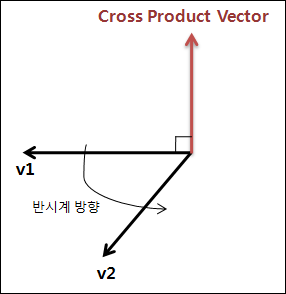
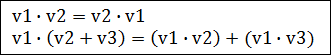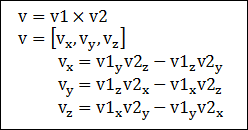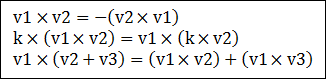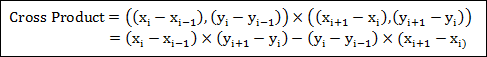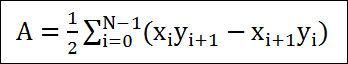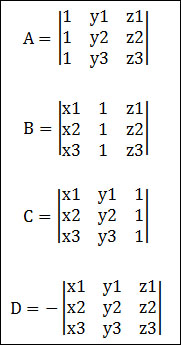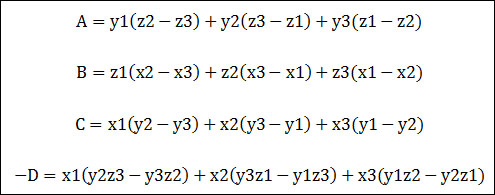두 개의 벡터에 대한 내적의 연산 결과는 스칼라 값입니다. 두 벡터 사이의 코사인값을 얻는 것은 간단합니다. 아래의 식은 두 벡터 v1, v2에 대한 내적 v를 계산하기 위한 필요한 단계를 보여주고 있습니다. 내적의 연산은 일반적으로 ‘ ∙ ‘ 로 표시합니다.

벡터 v1과 v2 사이의 각도로 표시하는 방법으로 하면 다음처럼 나타낼 수 있습니다.

위의 식으로부터 우리는 두 벡터중에 하나라도 크기가 0이면 내적 역시 0이 된다는 것을 알 수 있으며 두 벡터가 수직(90도)일 경우도 내적이 0이라는 것을 알 수 있습니다. 아래는 내적에 대한 몇가지 성질입니다. 즉, 교환법칙과 분배법칙 모두 성립한다는 것입니다.

두개의 벡터에 대한 외적은 또 하나의 새로운 벡터를 정의합니다. 두개의 벡터가 이루는 하나의 평면에 대해 수직인 벡터가 바로 외적에 의해 만들어지는 새로운 벡터입니다. 외적은 두 벡터가 이루는 각을 구하는 것이라든지, 광원에 대한 계산, 즉 빛의 방향을 구하는 계산 등에 응용됩니다.

아래의 공식은 두개의 벡터 v1, v2에 대한 외적 v를 구하기 위해 필요한 과정을 보여주고 있습니다. 외적 연산의 기호는 ‘ X ‘를 일반적으로 많이 사용합니다.

벡터 v1과 v2의 시작점을 원점이라고 할때, 벡터v1과 v2가 이루는 평면이 X축과 Z축이 구성하는 평면인 XZ라고 하면 외적에 의한 벡터는 v1에서 v2가 반시계방향이면 Y축 방향으로 위를 향하고 시계방향이면 Y축 방향으로 아래를 향합니다. 두 벡터의 외적에 대한 일반적인 성질은 아래와 같습니다. 내적과는 다르게 외적은 교환법칙이 성립하지 않습니다. 아래의 식에서 k는 스칼라값입니다.

벡터v1과 v2가 이루는 사인각으로도 외적을 표시할 수 있으며, 다음과 같습니다.

위의 식에서 a가 두벡터 사이의 각도 입니다. 위 공식에서 보듯, 외적도 내적과 마찬가지로 두 벡터가 이루는 각을 구하는데 사용할 수 있습니다.

폴리곤이 오목한지 볼록한지에 대한 각각의 경에 대해서, 좌표가 시계방향으로 되어 있는지, 반시계 방향으로 되어 있는지를 검사하기 위한 방법입니다. GIS에서 폴리곤 도형에 대해 시계방향인지 반시계방향인지에 따라 폴리곤에 대한 구멍(Hole)인지의 여부를 결정짓는 경우가 있습니다. 이외에 폴리곤의 앞면인지 뒷면인지의 여부도 시계방향인지의 여부에 따라 결정됩니다.

먼저 폴리곤의 구성하는 좌표의 개수가 N개라고 하고, 구성 좌표를 아래처럼 표기합니다.

볼록한 폴리곤에 대해서 좌표의 방향에 대한 간단한 검사는 인접한 좌표들이 이루는 선분(벡터)에 대한 외적(Cross Product)을 통해 가능합니다. 만약에 외적이 양수이면 수직벡터가 폴리곤이 이루는 평면(z축이 평면의 위쪽으로 향한다고 가정) 윗 방향이고, 음수이면 평면의 안쪽 즉 평면에 대해 아래 방향으로 향합니다.

오목한 폴리곤의 경우는 폴리곤의 면적을 계산함으로써 알 수가 있습니다. 면적을 계산하는 공식은 다음과 같습니다. (왜 이렇게 되는지는 블로그의 다른 글을 통해 곧 소개 하겠습니다)

위의 값이 양수이면 폴리곤의 구성 좌표의 구성 순서가 시계 반대 방향이고, 음수이면 시계 방향임을 나타냅니다.

이제 그렇다면, 뒤집어서…. 폴리곤이 오목한지 볼록한지는 어떻게 알 수 있을까요? 그것은 볼록한 폴리곤을 이루는 인접한 선분 벡터들은 모두 같은 부호이지만, 오목한 폴리곤의 경우는 부호가 섞여 있다는 것으로 알 수 있습니다.